《FPGA并行编程》读书笔记(第一期)04_DFT
《FPGA并行编程》读书笔记(第一期)04_DFT
- 1. 绪论
- 2. 读书笔记源说明
- 3. 6个Solution带你学习矩阵乘法加速
- 3.1 工程组织结构
- 3.2 S1_Baseline
- 3.3 S2_Manual_UNROLL与S3_Auto_UNROLL
- 3.4 S4_ARRAY_PARTITION与S5_PIPELINE
- 3.5 S6_Unit_PIPELINE
- 3.6 小结
- 4. 5个Solution带你学习DFT运算加速
- 4.1 工程组织结构
- 4.2 S1_Baseline
- 4.3 S2_SPipeline与S3_Loop_Interchange
- 4.4 S4_LUT
- 4.5 S5_Manual_Unroll
- 4.6 小结
1. 绪论
本章介绍了DFT,并将重点放在了介绍了DFT在FPGA实现中的算法优化。 DFT运算的核心是以一组固定系数执行矩阵向量乘法,因此首先进行矩阵乘法的优化策略分析后进行DFT算法的优化。
DFT算法的相关知识大家自行在书籍中查阅,我在这里就不班门弄斧了。
大家切记先把原理搞懂,算法加速只是工具,理解清楚算法内部的原理才是加速的核心。
大家切记先把原理搞懂,算法加速只是工具,理解清楚算法内部的原理才是加速的核心。
大家切记先把原理搞懂,算法加速只是工具,理解清楚算法内部的原理才是加速的核心。
2. 读书笔记源说明
本章内容的源代码见PP4FPGAS_Study_Notes_S1C04_HLS_DFT

3. 6个Solution带你学习矩阵乘法加速
3.1 工程组织结构
本小节一共有6个Solution,来对矩阵乘法进行优化。做实验之前,先把课本上的背景知识认真阅读下!

3.2 S1_Baseline
根据算法抽象出来的基础代码如下。
//*********************S1_Baseline
#ifdef S1_Baseline
void matrix_vector(BaseType M[SIZE][SIZE], BaseType V_In[SIZE], BaseType V_Out[SIZE]) {
BaseType i, j;
data_loop:
for (i = 0; i < SIZE; i++) {
BaseType sum = 0;
dot_product_loop:
for (j = 0; j < SIZE; j++) {
sum += V_In[j] * M[i][j];
}
V_Out[i] = sum;
}
}
#endif
首先对基础代码进行仿真,保证算法的正确性。

从上图可以看出算法正确,那么可以进行后面的优化工作。
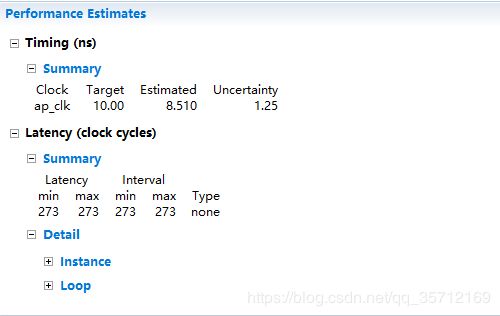
可以看出该代码的执行效率非常低,那么小的矩阵运算尽然还要花费2.73us之久,后面我们逐渐对它进行优化。
3.3 S2_Manual_UNROLL与S3_Auto_UNROLL
为了让大家回忆起以前用过的循环展开,这里面再把代码贴出。
//*********************S2_Manual_UNROLL
#ifdef S2_Manual_UNROLL
void matrix_vector(BaseType M[SIZE][SIZE], BaseType V_In[SIZE], BaseType V_Out[SIZE]) {
BaseType i, j;
data_loop:
for (i = 0; i < SIZE; i++) {
BaseType sum = 0;
V_Out[i] = V_In[0] * M[i][0] + V_In[1] * M[i][1] + V_In[2] * M[i][2] +
V_In[3] * M[i][3] + V_In[4] * M[i][4] + V_In[5] * M[i][5] +
V_In[6] * M[i][6] + V_In[7] * M[i][7];
}
}
#endif
//*********************S3_Auto_UNROLL
#ifdef S3_Auto_UNROLL
void matrix_vector(BaseType M[SIZE][SIZE], BaseType V_In[SIZE], BaseType V_Out[SIZE]) {
BaseType i, j;
data_loop:
for (i = 0; i < SIZE; i++) {
BaseType sum = 0;
dot_product_loop:
for (j = 0; j < SIZE; j++) {
#pragma HLS UNROLL skip_exit_check
sum += V_In[j] * M[i][j];
}
V_Out[i] = sum;
}
}
#endif
首先进行我们之前用过的循环展开,可以看出手动循环与自动循环展开的效果一样。
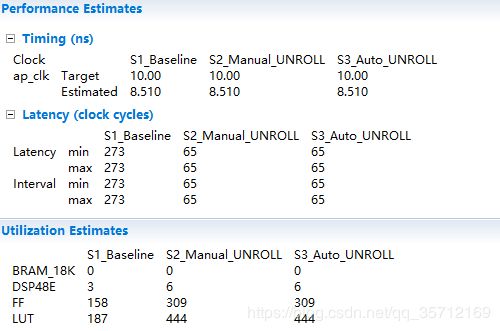
效率提升了4倍及以上,资源占用仅提高了两倍,但是大家有没有发现效率的提升并没有想象中的那么大呢,这是因为输入数据并不可以同时访问,从Analysis界面也可以看出端倪。
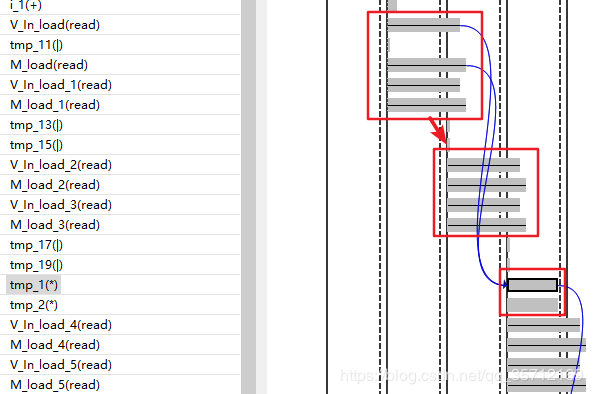
这里面并没有展现出完全的并行效果,这和数据的输入方式有关系。在没有指定的情况下这些数据就相当于用双端口BRAM存储,同一时间只能访问两个地址的数据。这里面还隐藏着一些计算单元的流水,对资源利用率高,后面会有专门的Solution进行介绍。

从资源界面可以看出,仅仅例化了2个乘法。

这些运算单元利用PIPELINE可以提高资源的利用率,后面会细说。那么如何实现下图高度并行的算法呢?S4_ARRAY_PARTITION给您带来解答。

3.4 S4_ARRAY_PARTITION与S5_PIPELINE
大家不要忘了,我第二章节讲解的ARRAY_PARTITION,这个优化策略可以实现课本图片对应的并行算法,在此之上在运用PIPELINE来进一步提高算法效率。

观察综合结果

运行效率确实提升了不少,现在仅需要0.13us就可以实现简单的矩阵乘法,速度提升了20倍以上。但不知大家是否发现了一个这样的问题,DSP资源占用了24个,虽然我们使用的ZYNQ7020资源非常丰富具有220个DSP资源,但是为了一个简单的运算竟然占用了10%的DSP资源,在我看来着实不是很实惠。下面介绍功能单元的流水,来进一步提高资源的利用率,大家在资源与速度方面来进行权衡。
3.5 S6_Unit_PIPELINE
代码如下

这里面PIPELINE的II的数值与指定的ARRAY_PARTITION的factor参数大小有关系。还有大家要注意数组利用资源的方式要注意,这里就先不给小伙伴们提及了。
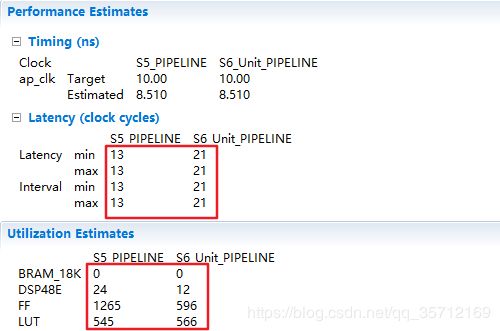
可以通过综合结果看出资源占用减少了,但同时算法运行的Latency也增加了,这就是前面经常所说的用时间换面积,均衡时间与资源实现目标。
分析Analysis界面可以发现,实现了功能模块级别的PIPELINE,提高资源的利用率。

大家可以自发的尝试factor与II的数值,来加深对PIPELINE的理解。现在小伙伴们应该要掌握的是,我们可以在算法级别、循环级别与功能级别等多个层次上进行流水线操作。另外要提的是,提高资源利用率的重点在要尽可能的提高运算单元的使用频率,不让它们有一丝一毫的空闲时间,实现资源利用最大化。
3.6 小结
本小节是利用UNROLL、ARRAY_PARTITION、PIPELINE来提高矩阵运算的效率,但由于资源的限制,小伙伴们要适时的牺牲Latency,来降低资源的使用。另外本小节提及的的新知识是单元的PIPELINE,通过压榨运算单元的空闲时间,进一步提高运算单元的使用效率,达到时间与空间的均衡。
4. 5个Solution带你学习DFT运算加速
4.1 工程组织结构

本小节一共有5个Solution来带领小伙伴们学习DFT运算加速,大家学习之前,千万要仔细阅读课本的原理知识。
4.2 S1_Baseline
#ifdef S1_Baseline
//*****************S1_Baseline
void dft(DTYPE sample_real[SIZE], DTYPE sample_imag[SIZE]) {
int i, j;
DTYPE w;
DTYPE c, s;
// Temporary arrays to hold the intermediate frequency domain results
DTYPE temp_real[SIZE];
DTYPE temp_imag[SIZE];
// Calculate each frequency domain sample iteratively
dft_each_Calculate:
for (i = 0; i < SIZE; i += 1) {
temp_real[i] = 0;
temp_imag[i] = 0;
// (2 * pi * i)/N
w = (-2.0 * 3.141592653589 / SIZE) * (DTYPE)i;
// Calculate the jth frequency sample sequentially
dft_jthCalculate:
for (j = 0; j < SIZE; j += 1) {
// Utilize HLS tool to calculate sine and cosine values
c = cos(j * w);
s = sin(j * w);
// Multiply the current phasor with the appropriate input sample and keep
// running sum
temp_real[i] += (sample_real[j] * c - sample_imag[j] * s);
temp_imag[i] += (sample_real[j] * s + sample_imag[j] * c);
}
}
// Perform an inplace DFT, i.e., copy result into the input arrays
ARRAY_Copy:
for (i = 0; i < SIZE; i += 1) {
sample_real[i] = temp_real[i];
sample_imag[i] = temp_imag[i];
}
}
#endif
首先对该代码进行仿真,验证由算法抽象出来的代码的正确性。

代码的运算精度符合要求,该代码符合要求。综合结果如下。

发现256点的DFT运算竟然需要46ms之多,这个代码CPU进行运算的话会快很多,为啥号称运算效率极高的FPGA运算竟需要如此长的时间。经过我们接下来的优化,你们会发现FPGA的神奇之处,可以将运算效率提高到这种地步。
4.3 S2_SPipeline与S3_Loop_Interchange
首先我们对代码的内层循环加入PIPELINE。
综合后发现代码的Latency确实减少了不少。
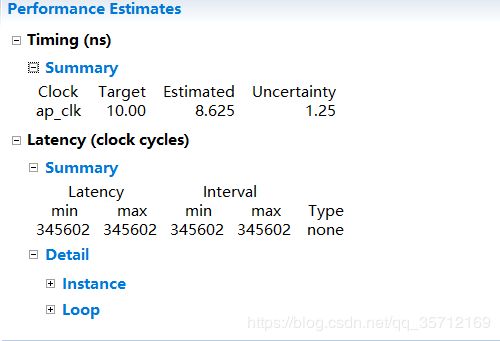
但同时发现Console中、Warning等均出现一个警告之类的东西。

PIPELINE仅仅只有II=5才可以实现流水,分析代码发现是因为内层循环因为循环之间都需要对同一个值进行读取和写入,因此才造成效率的降低,因此我们这里要考虑如何重构代码来解除这个限制。
这里我仅仅给大家提供几个关键点,具体理解还需大家读懂书中的内容。
- 我们使用的方法被称为循环交换与流水线交织处理,通过交换内层循环与外层循环,来解决限制。
- S矩阵是对角对称的,也是能够循环交换的前提条件。
- 仔细理解下面这张图,对理解如何进行循环交换代码非常重要。

经过循环交换后的代码如下
#ifdef S3_Loop_Interchange
//*****************S3_Loop_Interchange
void dft(DTYPE sample_real[SIZE], DTYPE sample_imag[SIZE]) {
int i, j;
DTYPE w;
DTYPE c, s;
// Temporary arrays to hold the intermediate frequency domain results
DTYPE temp_real[SIZE]={0};
DTYPE temp_imag[SIZE]={0};
// Calculate the jth frequency sample sequentially
dft_jthCalculate:
for (j = 0; j < SIZE; j += 1) {
// (2 * pi * i)/N
w = (-2.0 * 3.141592653589 / SIZE) * (DTYPE)j;
// Calculate each frequency domain sample iteratively
dft_each_Calculate:
for (i = 0; i < SIZE; i += 1) {
#pragma HLS PIPELINE II=1
// Utilize HLS tool to calculate sine and cosine values
c = cos(i * w);
s = sin(i * w);
// Multiply the current phasor with the appropriate input sample and keep
// running sum
temp_real[i] += (sample_real[j] * c - sample_imag[j] * s);
temp_imag[i] += (sample_real[j] * s + sample_imag[j] * c);
}
}
// Perform an inplace DFT, i.e., copy result into the input arrays
ARRAY_Copy:
for (i = 0; i < SIZE; i += 1) {
#pragma HLS PIPELINE II=1
sample_real[i] = temp_real[i];
sample_imag[i] = temp_imag[i];
}
}
#endif
小伙伴们可要仔细研究代码哦,初始代码如何经过循环交换转成上图的代码才是算法加速的精髓!现在我们对综合结果对比下,发现Latency减少为原来的1/80!

现在大家认为进行256点DFT运算是CPU效率高还是FPGA效率高?但是现在还存在着一个重大的问题。看综合报告可以看出,资源占用率太高了!!!

这时候我们就要分析原因了,看到底是哪个地方占用那么多的资源。

原来sin、cos的计算是罪魁祸首,这时候我们就要想利用什么方案才可以解决这个问题呢?大家可能想到利用咱们第二章学到的CORDIC可以极大的提高sin、cos的计算效率,这里我们没有采用这个方案,感兴趣的小伙伴可以尝试下。我们本次采用的方案是利用好S矩阵的优势,利用查找表的方案实现sin、cos的计算,具体细节见下一小节。
4.4 S4_LUT
小伙伴们观察下这个S矩阵
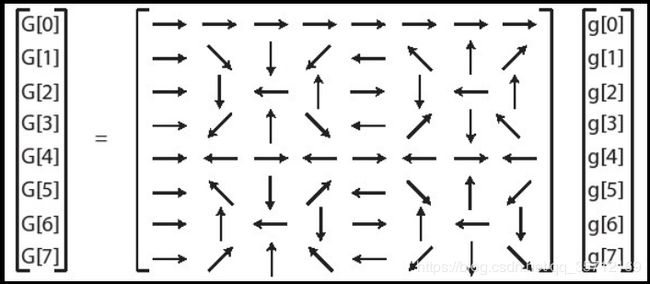
大家有没有发现S矩阵中的这些向量有非常多重复的向量,我们可以发现,第二行S[1][ ]相对应的向量覆盖了来自其他行的所有向量。可以利用这个特性来设计程序。具体重构代码的思路我就不多说了,重构后代码如下。

需要注意的地方已经标注,大家好好体会下,不会的可以后台联系我。综合后报告对比如下图。

发现资源利用减少10余倍之多,四不四非常神奇。大家可能还想继续减少Latency,依靠目前学过的优化策略那就只能牺牲面积来换速度了。
4.5 S5_Manual_Unroll
手动展开代码如下图所示。
#ifdef S5_Manual_Unroll
//*****************S5_Manual_Unroll
#include"coefficients256.h"
#include "ap_int.h"
void dft(DTYPE sample_real[SIZE], DTYPE sample_imag[SIZE]) {
int i, j;
DTYPE c_0, s_0;
DTYPE c_1, s_1;
// Temporary arrays to hold the intermediate frequency domain results
DTYPE temp_real[SIZE]={0};
DTYPE temp_imag[SIZE]={0};
// Calculate the jth frequency sample sequentially
dft_jthCalculate:
for (j = 0; j < SIZE; j += 2) {
// Calculate each frequency domain sample iteratively
dft_each_Calculate:
for (i = 0; i < SIZE; i += 1) {
#pragma HLS PIPELINE II=1
// Utilize HLS tool to calculate sine and cosine values
c_0 = cos_coefficients_table[(ap_uint<8>)(i * j)];
s_0 = sin_coefficients_table[(ap_uint<8>)(i * j)];
c_1 = cos_coefficients_table[(ap_uint<8>)((i) * (j+1))];
s_1 = sin_coefficients_table[(ap_uint<8>)((i) * (j+1))];
// Multiply the current phasor with the appropriate input sample and keep
// running sum
temp_real[i] += (sample_real[j] * c_0 - sample_imag[j] * s_0) +
(sample_real[j + 1] * c_1 - sample_imag[j + 1] * s_1);
temp_imag[i] += (sample_real[j] * s_0 + sample_imag[j] * c_0) +
(sample_real[j + 1] * s_1 + sample_imag[j + 1] * c_1);
}
}
// Perform an inplace DFT, i.e., copy result into the input arrays
ARRAY_Copy:
for (i = 0; i < SIZE; i += 1) {
#pragma HLS PIPELINE II=1
sample_real[i] = temp_real[i];
sample_imag[i] = temp_imag[i];
}
}
#endif
通过综合报告可以看出虽然速度增加一半,但是资源占用也同时增加了一半,面积与速度需要大家权衡。

4.6 小结
本小节我们进行了DFT算法的加速实验,从综合报告对比来看,在资源占用比较小的情况下,可以将速度提高160倍以上。本小节重点是对DFT算法的理解、DFT算法的循环交换、DFT算法中S矩阵的查找表策略、依据实现目标在速度与面积上取得均衡,小伙伴们这些知识都掌握了吗?
原创不易,切勿剽窃!
欢迎大家关注我创建的微信公众号——小白仓库
原创经验资料分享:包含但不仅限于FPGA、ARM、RISC-V、Linux、LabVIEW等软硬件开发。目的是建立一个平台记录学习过的知识,并分享出来自认为有用的与感兴趣的道友相互交流进步。
