matlab中窗函数的使用(一)

窗函数是频谱分析中一个重要的部分，窗函数修正了由于信号的非周期性并减小了频谱中由于泄露而带来的测量不准确性。

快速傅里叶变换假定了时间信号是周期无限的。但在分析时，我们往往只截取其中的一部分，因此需要加窗以减小泄露。窗函数可以加在时域，也可以加在频域上，但在时域上加窗更为普遍。截断效应带来了泄漏，窗函数是为了减小这个截断效应，其设计成一组加权系数。例如，一个窗函数可以定义为：
w(t)=g(t)       -T/2 w(t)=0          其他

g(t)是窗函数，T是窗函数的时间.

待分析的数据x(t)则表示为：

x(t)=w(t)*x(t)'

x(t)'表示原始信号,x(t)表示待分析信号。

 

加窗在时域上表现的是点乘，因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程。这个平滑过程可以被看出是由一组具有特定函数形状的滤波器，因此，原始信号中在某一频率点上的能量会结合滤波器的形状表现出来，从而减小泄漏。基于这个原理，人们通常在时域上直接加窗。

大多数的信号分析仪一般使用矩形窗（rectangular），汉宁（hann），flattop和其他的一些窗函数。

矩形窗函数：
w(k)=1

汉宁窗：     
w(k)=0.5*(1-cos(2*pi*k/(N-1)))     0<=k<=N-1

由于加窗计算中衰减了原始信号的部分能量，因此对于最后的结果还需要加上修正系数。在线性谱分析中，一般使用幅度系数（amplitude correction），在功率谱中，一般使用能量系数（energycorrection）。(这段不清楚在实际中如何用)

 

matlab中提供了很多窗函数，如下

 

还提供了显示窗函数的GUI工具，如wvtool可以显示用来显示窗的形状和频域图形，wintool可以打开窗设计和分析工具，如运行

wvtool(hamming(64),hann(64),gausswin(64))

可以对比汉明窗、汉宁窗和高斯窗

 

 

简单测试一下加窗的效果如下

 

 

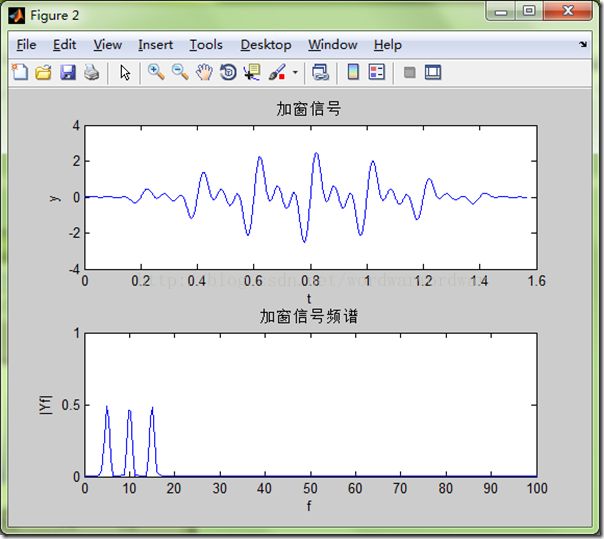
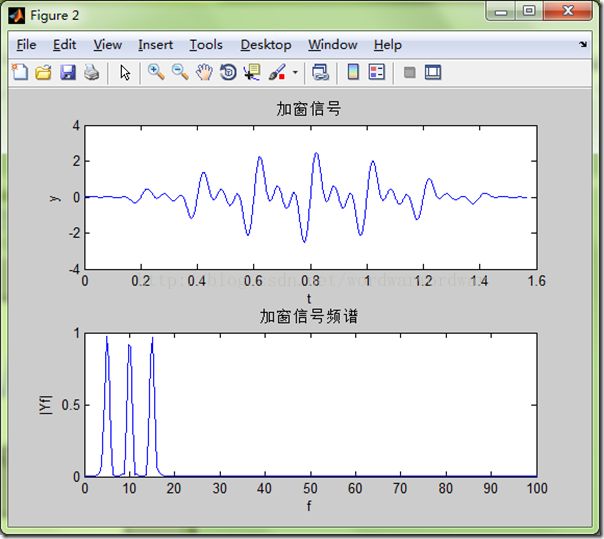
可以看到加窗后，频谱泄露确实减少了，但同时信号能量也减小了，这也许就是所说的要使用能量系数吧，如下，这样一来，对比就更明显了，加窗可以有效的减少频谱泄露。

 

 

测试代码如下

%% 窗函数测试
function main
clc
close all

Ts = 0.001;
Fs = 1/Ts;
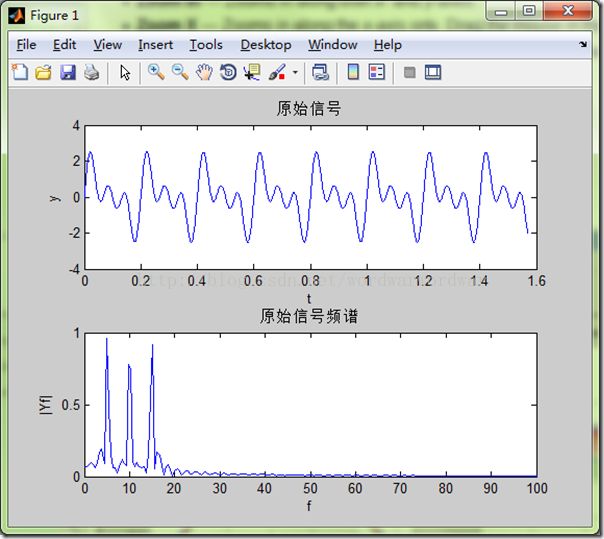
%% 原始信号
t = 0:Ts:pi/2;
yt = sin(2*pi*5*t) + sin(2*pi*10*t) + sin(2*pi*15*t);
[Yf, f] = Spectrum_Calc(yt, Fs);

figure
subplot(211)
plot(t, yt)
xlabel('t')
ylabel('y')
title('原始信号')
subplot(212)
plot(f, Yf)
xlabel('f')
ylabel('|Yf|')
xlim([0 100])
ylim([0 1])
title('原始信号频谱')

%% 加窗信号
win = hann(length(t));
yt1 = yt.*win';
[Yf1, f1] = Spectrum_Calc(yt1, Fs);

figure
subplot(211)
plot(t, yt1)
xlabel('t')
ylabel('y')
title('加窗信号')
subplot(212)
plot(f1, 2*Yf1) % 2表示能量系数
xlabel('f')
ylabel('|Yf|')
xlim([0 100])
ylim([0 1])
title('加窗信号频谱')
end

%% 求取频谱
function [Yf, f] = Spectrum_Calc(yt, Fs)
L = length(yt);

NFFT = 2^nextpow2(L);
Yf = fft(yt,NFFT)/L;

Yf = 2*abs(Yf(1:NFFT/2+1));
f = Fs/2*linspace(0,1,NFFT/2+1);
end