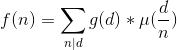[2020 年联考 A 卷] 作业题 （莫比乌斯反演+变元矩阵树定理）

题面：https://www.luogu.com.cn/problem/P6624

 

 

题解

一道套路题

先来考虑gcd=1的情况

如何求所有生成树的边权和？

使用变元矩阵树，把每一条边的边权赋为1+wx（w为它原来的边权）

然后求其在mod x^2意义下的答案

那么x项的系数就是所有生成树的边权和

因为要得到x项，只能有一条边贡献出自己的边权，其它的边都只能贡献1

所以这样做是可以求出生成树的边权和的

我们可以对矩阵上的数维护二元组

如何求逆元呢？

那么两边除一个a^2

所以a+bx的逆元为

其它的加减乘法稍微重载一下就好了

 

再来考虑gcd不一定为1的情况

我们设f(n)表示边权gcd恰好为n时的生成树的边权和，这个不好直接统计

设g(n)表示边权gcd为n的倍数的生成树的边权和

于是有

那么

最后的答案就是∑i*f(i)（算上gcd的贡献）

就做完了

 

代码：

#include
#include
#include
#include
using namespace std;
#define N 35
const int mod=998244353;
int ksm(int x,int y)
{
	int ret=1;
	while(y){
		if(y&1)ret=1ll*ret*x%mod;
		y>>=1;x=1ll*x*x%mod;
	}
	return ret;
}
struct P{
	int x,y;
	P(){x=y=0;}
	P(int _x,int _y){x=_x;y=_y;}
	P operator + (const P &t)const{return P((x+t.x)%mod,(y+t.y)%mod);}
	P operator - (const P &t)const{return P((x+mod-t.x)%mod,(y+mod-t.y)%mod);}
	P operator * (const P &t)const{return P(1ll*x*t.x%mod,(1ll*x*t.y+1ll*y*t.x)%mod);}
}a[N][N];
P inv(P s){
	int ni=ksm(1ll*s.x*s.x%mod,mod-2);
	return P(1ll*s.x*ni%mod,1ll*(mod-s.y)*ni%mod);
}
P det(int n)
{
	int i,j,k;P ans=P(1,0);
	for(i=1;i<=n;i++){
		if(!a[i][i].x){
			for(j=i+1;j<=n;j++)
				if(a[j][i].x)break;
			if(j>n)return P(0,0);
			for(k=i;k<=n;k++)swap(a[i][k],a[j][k]);
		}
		for(j=i+1;j<=n;j++){
			P w=inv(a[i][i])*a[j][i];
			for(k=i;k<=n;k++)
				a[j][k]=a[j][k]-a[i][k]*w;
		}
	}
	for(i=1;i<=n;i++)ans=ans*a[i][i];
	return ans;
}
#define M 200005
int prime[M],tot,mu[M];
bool vis[M];
void shai()
{
	int i,j,n=200000;
	vis[1]=1;mu[1]=1;
	for(i=2;i<=n;i++){
		if(!vis[i]){
			prime[++tot]=i;
			mu[i]=-1;
		}
		for(j=1;j<=tot;j++){
			int tmp=i*prime[j];
			if(tmp>n)break;
			vis[tmp]=1;
			if(i%prime[j]==0){mu[tmp]=0;break;}
			mu[tmp]=(mod-mu[i])%mod;
		}
	}
}
struct node{int u,v,w;}tmp;
vector e[M];
int f[M],g[M];
int main()
{
	//freopen("count.in","r",stdin);
	//freopen("count.out","w",stdout);
	int n,m,i,j,k,u,v,w,mx=0;shai();
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&w);
		mx=max(mx,w);tmp.u=u;tmp.v=v;tmp.w=w;
		e[w].push_back(tmp);
	}
	for(i=1;i<=mx;i++){
		memset(a,0,sizeof(a));
		int cnt=0;
		for(j=i;j<=mx;j+=i){
			for(k=0;k<(int)e[j].size();k++){
				u=e[j][k].u;v=e[j][k].v;w=e[j][k].w;
				a[u][v]=P(mod-1,mod-w);
				a[v][u]=P(mod-1,mod-w);
				a[u][u]=a[u][u]+P(1,w);
				a[v][v]=a[v][v]+P(1,w);
				cnt++;
			}
		}
		if(cnt