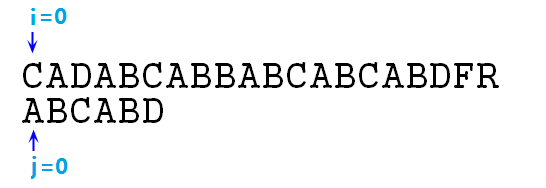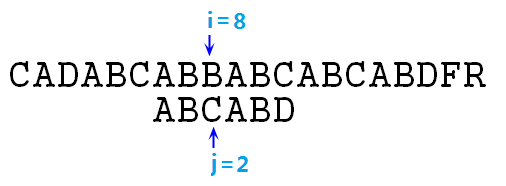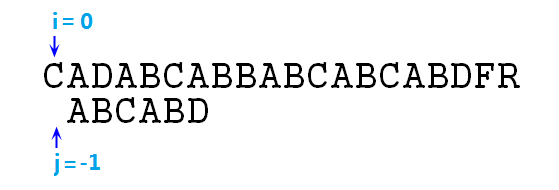数据结构与算法专题之串——字符串及KMP算法
本章是线性表的最后一部分——串。其实串就是我们日常所说的字符串,它是一系列结点组成的一个线性表,每一个结点存储一个字符。我们知道C语言里并没有字符串这种数据类型,而是利用字符数组加以特殊处理(末尾加'\0')来表示一个字符串,事实上数据结构里的串就是一个存储了字符的链表,并且封装实现了各种字符串的常用操作。
串的概念和定义其实没什么好说的,本章的主要内容是KMP算法,也就是字符串模式匹配算法,本章后面会介绍到,我们下面所有提到的字符串均使用顺序结构,也就是字符数组。我们先来介绍字符串的一些常见的基本操作及实现。
串的常用操作
字符串的常用操作大部分都已经被C/C++的标准库实现了,我们下面直接介绍这几个C函数
1.字符串操作类
strcpy (s1, s2)
复制字符串,将s2的内容复制到s1,函数原型_CRTIMP char* __cdecl __MINGW_NOTHROW strcpy (char*, const char*),可以看出第二参数可以是常量也可以是变量,但第一参数必须是变量。这里要注意的是s2的内容长度(包括'\0')不能超出s1的总长度。该函数通常可以用来为字符数组赋值,示例(第3行可以认为是在给cpy赋值):
char str[233];
char cpy[233];
strcpy(cpy, "i am string");
strcpy(str, cpy);strncpy(p, p1, n)
复制指定长度字符串,与上一个函数类似,只不过多了第三个参数,指的是要拷贝的字符串的长度,此函数会将p1首地址开始的n个字节的内容拷贝到p中,需要注意的是,拷贝后的内容并不包含字符串结束标志'\0',所以需要手动添加才可使p变成需要的字符串,示例:
char str[233];
char cpy[233] = "i am string";
strncpy(str, cpy, 8);
str[8] = '\0';strcat(p, p1)
字符串连接 ,该函数会将p1的内容添加到p的末尾,比如p="Hello",p1="World",则执行该函数,p的内容变为"HelloWorld"。原型_CRTIMP char* __cdecl __MINGW_NOTHROW strcat (char*, const char*);同样第二参数可为常量,这里需要注意的是,p和p1必须都是合法字符串(即包含结束标志'\0')且需要保证连接后的总长度不会超过p的总大小。示例:
char str[233] = "Hello";
char cat[233] = "World";
strcat(str, cat);strncat(p, p1, n)
附加指定长度字符串,类似上面strcpy和strncpy的区别,这里也是一样的,截取p1前n个字节的内容添加到p的末尾,注意,此函数会覆盖p末尾的'\0',并在添加p1完成后自动在最后添加'\0',所以无需像上面那样手动加'\0'。示例:
char str[233] = "Hello";
char cat[233] = "Worldxxx";
strncat(str, cat, 5);strlen(p)
取字符串长度,这是我们最常用的一个函数了,得到字符串长度,没什么好说的,需要注意的是p必须为合法字符串,即有'\0',下文中若再次提到“合法字符串”即为“包含“'\0'”的字符串 。还有一点是,该函数返回值为字符串的字符数,要区别于字符串占用空间,比如对于字符串"love",它的长度为4,而占用空间为5,strlen对于此字符串的返回值即为4,示例:
char str[233] = "Hello";
int len = strlen(str);strcmp(p, p1)
比较字符串,即比较p与p1的字典序大小,如果p比p1小(p字典序靠前),则返回-1;若p比p1大(p字典序靠后),则返回1;若两字符串一样,则返回0。所谓的字典序,指的是将字符串首部对齐,从左到右依次比较对应位置的字符大小,直至找到第一个不一样的位置,其大小关系就是整个字符串的大小关系(如果大写与小写比较,则实际是比较其ASCII码),当然,如果比较到一个字符串结束还未有结果,则短的字符串靠前(想一下英文词典里单词的排序)。
例如"a"<"b","food"<"foot","hack">"back","hasak">"hasa","bbc">"abcd","Ask"<"ask"等……
该函数通常用于判断两字符串是否相等,两参数均可为常量,示例(该例子res值为-1):
char str[233] = "hello";
char cmp[233] = "world";
int res = strcmp(str, cmp);strcasecmp(p, p1)
忽略大小写比较字符串,与上一个函数是同样的功能,只不是上面是区别大小写的,这里是忽略大小写,也就是说,此函数认为'a'和'A'是相等的,也就是说字符串"abCdEFGhiJ"和"AbCDEfgHij"是相等的,返回值为0,示例(此例res为0)
char str[233] = "HEllo";
char cmp[233] = "hELlo";
int res = strcasecmp(str, cmp);strchr(p, c)
在字符串中查找指定字符, 即在p中从左向右查找第一次出现字符c的位置(找不到就返回NULL),参数c可为字符或表示ASCII码的整型。需要注意的是该函数的返回值并非下标整数值,而是一个代表该位置的地址,所以我们需要减去p的首地址即可得到该字符第一次出现的下标值。示例(下例res值为4):
char str[233] = "Hello world";
char ch = 'o';
int res = strchr(str, ch) - str;strrchr(p, c)
在字符串中反向查找指定字符, 与上一个函数功能一致,只不过这个是从右向左查找第一次出现的位置(返回值也是该位置的地址,找不到则NULL),同样需要减去首地址来获取索引下标值,示例(该res值为7):
char str[233] = "Hello world";
char ch = 'o';
int res = strrchr(str, ch) - str;strstr(p, p1)
查找字符串, 上述两个函数均是在字符串里查找字符,这个函数是从字符串查找字符串,也就是查找字符串的子串(找不到就返回NULL),在p中从左向右查找第一次匹配了p1的位置,比如p为"abcdabcd",p1为"bcd",则执行函数,返回值为第一次匹配的地方即蓝色的bcd中的b,同样是返回地址,需要减去首地址得到下标,示例(此res为2):
char str[233] = "Hello hello";
int res = strstr(str, "llo") - str;字符串与数的转换
atoi(p)
字符串转换到int型,该函数返回值为int,为p转换成int后的值,不过p必须要合法,例如字符串"123"可以转换成整数123,但是字符串"abc"不可以转换。示例:
int res = atoi("666");atof(p)
字符串转换到double型,与上面同理,转换成double型且必须合法。 示例:
double res = atof("123.45");atol(p)
字符串转换到long整型,示例:
long res = atol("666");atoll(p)
字符串转换成long long类型,long long即64位整型,示例:
long long res = atoll("666666666666666");下面就是本章的重点内容:KMP算法
字符串模式匹配KMP算法
***注意,下面的内容稍微有点难度,请注意仔细理解,切不可走马观花式的阅读。
前言
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。
字符串暴力匹配
我们引入问题:假设有一个字符串s,一个字符串p,我们要找到p在s中第一次出现的位置,那么应该如何寻找呢?我们第一反应应该是本文上半部分讲到的字符串操作函数strstr(s, p)来寻找字符串位置,那么我们不依赖已经实现好的函数,自己来实现解决应该如何处理呢?
首先想到的,就是将两字符串首端对齐,依次比较对应位置的字符,如果比对成功,则继续比较下一个字符;如果失败,那么就要把p字符串整体后移一个位置,重新开始比对对应位置的字符,直至p的所有字符都与s某段一一对应,匹配成功结束;否则匹配失败。
我们图解一个字符串匹配问题,假设有字符串s="CADABCABBABCABCABDFR",p="ABCABD",我们要寻找p在s中的位置,步骤分解如下 :
① 首先我们使用指针i与指针j分别作s与p的下标,先使得i=j=0,即将s[0]与p[0]对齐,并且比较s[i]与p[j],比对是否匹配,如图:
② 显然如上图,s[i]与p[j]不匹配,所以我们需要将p字符串整体右移一位,即i=1,j=0,如下图所示:
③ 此时s[i]与p[j]匹配,所以继续向下比较,即i和j同时右移,i=2,j=1,如下图所示:
④ 显然,此时s[i]与p[j]不匹配了,所以p字符串整体右移,并重新开始匹配,即i=2,j=0,如下图:
⑤ 此时不匹配,那么继续整体右移p字符串,如下图:
⑥ 此时s[i]=p[j]=A,可以继续匹配,i++,j++,s[i]=p[j]=B……直至i=8,j=5时,失去匹配,如下图:
⑦ 按照暴力匹配的思想,此时应该右移p字符串,即令i=4,j=0,重新开始匹配。我们可以发现i指针发生了回溯,且回溯了4个字符的位置!回溯重置后如下图:
⑧ 显然,此时的s[i]与p[j]必然失配,由于我们在上一次匹配中(即p[0]与s[3]对齐时),我们已经知道了p[0]=A,p[1]=s[4]=B,所以对于此时i=4,j=0来说,s[i]=p[j]是绝对不成立的,所以i指针回溯回来也没啥用,必然会失去匹配,i依然还要再次后移,浪费时间。那么我们就需要一种算法,使得在失去匹配时,i指针保持不动,直接移动j指针到相应位置即可,比如在第⑥步操作中,失去匹配后,i指针不动,直接将j指针置为2,如下图:
⑨ 这样,我们没有使i指针回溯,而是直接将p字符串移动了若干位,且保证了此时j指针前面的所有位置均匹配(s[6]=p[0]=A,s[7]=p[1]=B),我们现在只需要从现在的指针位置开始比较即可。这种跳跃式的匹配方式就是我们接下来要讲的KMP算法,此算法分析利用了p字符串的特点,保证了i指针的单向性,仅通过修改j的位置,即可使p串达到最合适的位置。
下面给出暴力匹配的代码:
int str_match(char *s, char *p) // 查找p在s中的位置
{
int i = 0;
int j = 0;
while(s[i] && p[j])
{
if(s[i] == p[j]) // 匹配,继续执行
{
i++;
j++;
}
else // 失去匹配,p后移
{
i = i - j + 1; // i-j代表此次匹配i的初始位置,再+1表示p后移
j = 0;
}
}
int len = strlen(p);
if(j == len) // j与len相等,说明p字符串匹配到结尾,即全部匹配成功
return i - j; // 返回第一个匹配的位置
return -1; // 无匹配,返回-1
}模式匹配KMP算法
在学习KMP算法之前,我们先需要准备大量的前置知识,篇幅很长,请耐心阅读学习。
字符串前缀后缀
何为前缀后缀?简单来说,将一个字符串在任意位置分开,得到的左边部分即为前缀,右边部分即为后缀。例如对于字符串"abcd",它的前缀有"a","ab","abc";后缀有"d","cd","bcd"。注意前后缀均不包括字符串本身。
最长公共前后缀
对于一个字符串来说,它既有前缀,又有后缀,所谓的最长公共前后缀,即该字符串最长的相等的前缀和后缀。例如上面的字符串"abcd"就没有公共前后缀,更别提最长了,因为它的前后缀里就没有相等的;而字符串"abcab"就有一个最长的公共前后缀即"ab"。
next数组
那么求最长公共前后缀到底有什么用呢?我们先来分析暴力解法中第⑥步的操作,我把图改了一下,请看图:
如图所示,当我们发现s[8]与p[5]失配的时候,暴力解法是令i=i-j+1,j=0,即p串右移一位。但更好的做法是保持i不变,j变为2,即让s[8]与j[2]对齐,也就是p右移3位。那么我们如何得到这个3位呢?也就是说,我们是怎么知道j要指向2呢?这就要用到我们的公共前后缀了。
注意上图,在此时失配,说明粉色框起来的部分是完全匹配的,那么绿色框与蓝色框匹配,而蓝色部分是p字符串粉色部分的后缀,红色部分为p字符串粉色部分的前缀,恰好这个红色部分与蓝色部分相等,也就是说,p的粉色部分,也就是当前匹配成功的部分,有相等的前后缀。既然蓝色匹配绿色 ,蓝色等于红色,那么红色必然匹配绿色,也就是说,我们只需将红色部分与绿色部分对齐,j指针指向红色部分的后一位,即可不更改i指针而继续匹配下去。而我们的j指针要移动到的位置2,恰好是这个公共前后缀的长度2,所以,我们得出以下结论:
当s[i]与p[j]失配时,计算不包括p[j]在内的左边子串(即p[0]~p[j-1])的最长公共前后缀的长度,假设长度为k,则j指针需要重置为k,i不变,继续匹配。
那么现在的问题就是求最长公共前后缀了,总不能每次失配都要求一次子串的最长公共前后缀吧?而且好像这个最长公共前后缀只与p有关呢。所以,我们引入了next数组,当p串在位置j失配的时候,需要将j指针重置为next[j],而next[j]就代表了p字符串的子串p[0~j-1]的最长公共前后缀,显然,next[0]无法求出(因为对于p[0]来说,它左边并没有子串),我们需要置为-1。
我们分解一个next数组的求解过程,对于字符串"ABCABD",先求其各子串的最长公共前后缀:
上表红色部分即为该子串的最长公共前后缀,根据上表,我们可得next数组:
可以看出,我们就是把next[0]初始化为-1,后面将最大公共元素长度列内的数据依次填入next数组即可,最大公共元素长度列最后一个数据舍弃。
那么如何用程序求解next数组?我们下面就来研究一下求法。
根据前面的学习可知,如果有k位前缀p[0~k-1]和k位后缀p[j-k~j-1]相等(当然,j>k),则有next[j]=k,这就意味着p[j]之前的子串中有长度为k的相同的前后缀,这样的话,我们在KMP匹配过程中,若在位置j发生了失配,则直接将j移动到next[j]的位置继续匹配,相当于p字符串移动了j-next[j]位,那么我们如何推出这个next来?我们需要遍历p这个模式串来确定next数组:
我们首先定义一个k和一个j,j用来从左到右遍历字符串,相当于是p当前子串的后缀的最右字符,而k指向了当前最长前缀的最右字符。初始的时候,我们知道next[0]=-1,所以k为-1,j为0。
① 若k=-1,说明当前字符j结尾的子串没有最长前后缀,则next[j + 1] = 0,j,k同时后移。
② 若p[j] == p[k],说明当前字符j结尾子串的前缀和后缀匹配了k+1位(由于k指下标,下标从0开始,所以要+1),即next[j+1] = k + 1(其实第①条也可以写成这样,毕竟-1+1=0嘛),然后j,k同时后移继续比较
③ 若p[j] != p[k],则说明当前字符j结尾的子串的后缀与前缀k不相同,所以需要将k向前移动再重新匹配。那么k要移动到哪里呢?我们想一下,既然我们能够走到p[j]与p[k]进行比较这一步,说明不包括p[k]在内的前k个字符一定与不包括p[j]在内的前k个字符一致,那么对于子串p[0~k-1]来说,next[k]代表了它的最长公共前后缀的长度,也就是说,不包括p[j]在内的前next[k]个字符一定与整个串的前next[k]个字符相同,比较难理解,我们图示一下:
如图所示,当p[j]与p[k]不匹配时,两红色箭头所框起来的部分是完全相同的,而对于左边那一段红色箭头框起来的部分,p[k]与p[next[k]](粉色与绿色)是肯定不相等的,但我们思考一下next[k]的含义是什么?对的,就是p[k]左边的串的最大公共前后缀的长度,也就是说,最左边两段蓝色区域是相同的,那么由于两个红色箭头框起来的部分相同,所以上图四片蓝色区域均互相相同,那么既然最右边的蓝色区域与最左边的蓝色区域相等,那么在p[j]与p[k]不相等的时候,只需要将k重置为next[k],即可保证此时的k与j仍有公共前后缀。但是需要注意的是,橙色区域一定与粉色区域不相等,粉色区域一定与绿色区域不相等,但是橙色区域与绿色区域关系未知,所以当j与k不匹配时,k应该置为next[k],继续比较,再不匹配再置为next[k]……
或许结合代码看一下就会明白:
void next_arr(char* p, int *next)
{
int len = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < len - 1)
{
//k表示前缀最后一位,j表示后缀最后一位
if (k == -1 || p[j] == p[k])
{
// 对应步骤1和2
++k;
++j;
next[j] = k;
// 以上三步可以简写成下面这样,结合自增特点思考一下
// next[++j] = ++k;
}
else // 失配时,移动k指针,即步骤3
{
k = next[k];
}
}
}根据next数组求解字符串匹配
我们已经学习了next数组的作用和求法,下面直接给出KMP算法利用next数组求解匹配的过程:
① 初始时i=j=0,即首部对齐。若s[i] == p[j] ,则字符匹配,i,j分别加1,继续循环执行;
② 若j == -1,则说明p串需从头匹配,则i++,j++,继续循环执行;
③ 若s[i] != s[j],则失配,j = next[j],继续循环执行。
④ 重复这些步骤直至i指针超过了s的最大长度或者j超过了p的最大长度
我们上面已经求得"ABCABD"的next数组为:
下面我们根据这个next数组和上述步骤来图解一下本章前面的"CADABCABBABCABCABDFR"与"ABCABD"的匹配问题:
① 首先i=j=0,对齐首端
② 上图可知,不匹配,则j=next[j],即j=-1,匹配过程变成如下图所示:
③ 事实上j=-1这一步相当于让p右移了一位而已,然后按照步骤,j==-1时应该同时移动i,j指针,如图:
④ 这里匹配,则根据求解步骤,应该同时移动i,j指针,来比较下一对字符,即p[1]=B和s[2]=D,失配,j=next[j],即j=0,如下图:
⑤ 依然不匹配,则j=next[j],即j=-1,注意,结合上步,我们这里连续使用next数组跳跃了两次,这里实际上是性能的损失,可以优化的,这点后面再说,然后此时j==-1,需要同时移动i,j指针,移动后如图所示:
⑥ 此时s[3]与p[0]匹配,指针增加继续向下比较,直至i=8,j=5时,B和D不匹配了,如图:
⑦ 此时需要使j=next[j],也就是j=2,相当于p字符串右移了3位,然后继续比较,如下图:
⑧ 此时依然失配,则j=next[j]=0,此时s[8]与p[0]仍然失配(所以说这个next其实还可以继续优化,不过没优化也比暴力快得多),j=next[j]=-1,终于可以右移i,j指针了,执行完本步骤以后如下图所示:
⑨ 此时匹配,指针增加,匹配,增加,匹配,增加……直至i=14,j=5时失配,则j=next[j]=2,如下图:
⑩ 此时匹配,指针增加,继续比较,还匹配,增加,比较,还匹配……直至i=17,j=5,依然是匹配的,然后指针再增加,i=18,j=6,此时发现j指针已经超出p字符串的范围了,结束步骤,并且说明p字符串已经成功匹配了s,如下图:
若由于i超出了s的最大长度,且此时j小于p的长度(也就是j没有过界)则说明未匹配。若匹配成功,则匹配的位置(返回值)为上图粉色框框的最左边字符的在s中的位置,即当前i指针的位置减去p的总长度即i-j=12。
根据上面的步骤可以看出,我们的i指针自始至终都在向右移动,并没有产生过回溯,因此相比较暴力解法而言,KMP算法的性能还是相当高的。
kmp匹配的过程代码如下:
int kmp_match(char *s, char *p, int *next)
{
next_arr(p, next);
int i = 0;
int j = 0;
while (s[i] && p[j])
{
// j = -1或字符匹配成功指针i,j后移
if (j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
{
// 匹配失败则移动j指针,相当于p字符串后移若干位
j = next[j];
}
}
int len = strlen(p);
if(j == len) // j与len相等,说明p字符串匹配到结尾,即全部匹配成功
return i - j; // 返回第一个匹配的位置
return -1; // 无匹配,返回-1
}以上就是kmp算法的基本内容,可以看出,kmp在处理较大的字符串匹配问题时效率是相当高的,并且kmp是ac自动机(Aho-Corasick automaton,多模匹配算法,后面或许会讲到)的基础知识,理解并掌握kmp是相当重要的。我们之前的讲解中说到next数组的性能问题,其实对于这个next数组,我们是可以继续优化的。具体优化原理及方法请看下一小节。
next数组的优化
这个……还是等我有时间再写吧,不要打我……
附加几个练习题传送门:
SDUT OJ 2272 数据结构实验之串一:KMP简单应用
SDUT OJ 2125 数据结构实验之串二:字符串匹配
SDUT OJ 3311 数据结构实验之串三:KMP应用
以上就是本章全部内容了,数据结构线性表部分全部结束,接下来的章节我们会开始讲解另外一种神奇的数据结构——树,欢迎大家继续跟进学习交流~
下集预告&传送门:数据结构与算法专题之树——树与二叉树的定义与性质