leetcode 第62题 不同路径, 第63题 不同路径 II, 第64题,最小路径和(python解法)
leetcode 第62题 不同路径, 第63题 不同路径 II, 第64题,最小路径和 (python解法)
问题解析
最近在写动态规划的题目,刷题时看到这三道题,觉得很有意思。这三题的内容基本差不多,可以看成时迷宫问题(但是要简单的多,因为可以移动的方向只有两个,向下或向右),所以用动态规划解比较方便。
第62题: 不同路径
它给定两个整数代表移动网格的大小,所以我们可以先利用生成一个与网格大小相等的二维数组,这个数组每一个数是索引代表位置的路径数。由于只能向下或者向右移动,所以对于数组的最后一列上所有的位置,都只能向下移动,因此这些位置的数都先设为1。同理,由于只能向右移动,那么最后一行的数也全部设为1(如下图所示)。
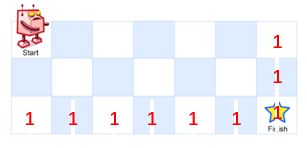
设置好这些后,下面开始遍历,从倒数第二行和倒数第二列开始,前面说过某个位置的路径数等于下面位置与右边位置路径和相加,所以可以写出状态转移方程为dp[i][j] = dp[i-1][j] + dp[i][j-1]。由这个转移方程就可以写出所有的位置的路径数了。最后的结果如下:

最后只要输出dp[0][0],就OK了。
扩展
上面这个是一种常规解法,用的是动态规划,下面介绍一种更为直观的思路,利用排列组合来解题。
首先,有一点我们是可以确定的,那就是机器人从起点到终点总共要走m+n-2步,其中m-1步向左,n-1步向下(m代表列数,n代表行数)。那么问题就可以简化成从m+n-2步中挑选出m-1步出来,共有多少种挑选法?(可以类比成m+n-2个人排成一排,从中挑选出m-1个人出来的方法数) 弄清楚这点,就可以一步解出结果。结果为:
![]()
第63题:不同路径 II
这一题相比较上一题加了一个条件,即在数组中设置了障碍物,存在障碍物的位置不能移动,也就是所有可行的路线在这里中断。首先,先看两个比较特殊的情况,那就是终点或者起点存在障碍物,这样话就不用计算而直接返回零。
接下来看看最后一列和最后一行。最后一列,如果某个位置上存在障碍物,由于这一列只能向下移动,所以该位置向上所有的位置都不能到达终点,全部设为零,其它的能够到达的先设为零。最后一行也是如此。
其它的位置在遍历时分两种情况:一种是当前位置上存在障碍物,那么就直接设为零,即无法到达终点。第二种是当前位置没有障碍物,那么就和第62题一样的操作。所以状态转移方程为:

假设网格中存在三个障碍物,如图所示,最后一行和最后一列的路线就可以写出来。
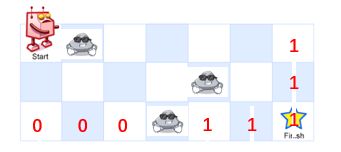
接下来就可以开始遍历了,下面是最后的结果图:

恰好最后的结果等于零。
这一题我们可以不开辟一个新的空间来存储dp这个二维数组,而直接在题目所给的数组上操作。这可能有点绕,因为数组中1代表障碍物。在操作原数组最后一行和最后一列时,如果出现1,那么就将1上面的位置或者前面的位置(包括当前位置)全部设为零(说明这些位置到达终点的路径数是零)。其余的位置设为1。而在遍历数组的过程中,如果遇到1,说明此处由障碍物,直接改为0。
第64题 最小路径和
其实第63题可以看成是64题一个小小的变形。我们也可以不用开辟新的空间,直接在原数组上操作。由于只能向下或向右,所以数组的最后一行只有一个移动方向,所以最后一行每个位置的路径和就等于当前位置的数直接加上后面一个位置的路径和。最后一列也是这样。
从倒数第二行和倒数第二列开始,每个位置上的数要加上下面的位置和右边的位置中较小的数,这样就实现了最小的路径和,状态转移方程可以写为:dp[i][j] += min(dp[i-1][j], dp[i][j-1])。这样遍历到最后,dp[0][0]代表的就是最小的路径和。
源码
第62题: 不同路径
from math import factorial
class Solution:
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
# 中规中矩,动态规划
# dp = [[1 if i == m-1 or j == n-1 else 0 for i in range(m)] for j in range(n)]
# print(dp)
# for i in range(m-2, -1, -1):
# for j in range(n-2, -1, -1):
# print(i, j)
# dp[j][i] = dp[j+1][i] + dp[j][i+1]
# print(dp)
# return dp[0][0]
# 注意,前方高能。使用排列组合。
return int(factorial(m + n - 2) / factorial(m -1) / factorial(n-1))
第63题:不同路径 II
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
if obstacleGrid[-1][-1] or obstacleGrid[0][0]: # 最特殊的情况,终点或起点被阻挡,那么总路线等于零
return 0
m = len(obstacleGrid)
n = len(obstacleGrid[0])
for i in range(m-1, -1, -1): # 检查最后一列,如果出现1,则该位置上面的所有的位置都设为零
if obstacleGrid[i][n-1] == 0:
obstacleGrid[i][n-1] = 1
else:
for i1 in range(i, -1, -1):
obstacleGrid[i1][n-1] = 0
break
print(obstacleGrid)
for j in range(n-2, -1, -1): # 检查最后一行,如果出现1,则该位置前面的所有的位置都是无法通过的,所以路线为1
if obstacleGrid[m-1][j] == 0:
obstacleGrid[m-1][j] = 1
else:
for j1 in range(j, -1, -1):
obstacleGrid[m-1][j1] = 0
break
print(obstacleGrid)
for i in range(m-2, -1, -1):
for j in range(n-2, -1, -1):
obstacleGrid[i][j] = 0 if obstacleGrid[i][j] == 1 else obstacleGrid[i+1][j] + obstacleGrid[i][j+1]
print(obstacleGrid)
return obstacleGrid[0][0]
第64题 最小路径和
class Solution:
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
m = len(grid)
n = len(grid[0])
for i in range(m-2, -1, -1):
grid[i][n-1] += grid[i+1][n-1]
for j in range(n-2, -1, -1):
grid[m-1][j] += grid[m-1][j+1]
for i in range(m-2, -1, -1):
for j in range(n-2, -1, -1):
grid[i][j] += min(grid[i+1][j], grid[i][j+1])
print(grid)
return grid[0][0]
