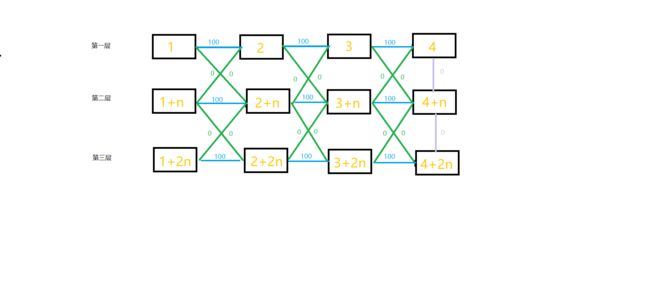
分层图
讲真的...感觉有点像那么一点点的种类并查集
简单来说,就是把一个图分成很多层,然后对图进行一些处理
比较模板一点的东西就是直接在分层图上跑最短路,这个时候就涉及到了很多决策,每一个决策能进行一些特殊的操作,比如让某条边免费(边权为0,不是把边切掉),让某条边花费减半之类的,这个时候就可以用分层图了
然后讲讲分层图的具体实现。首先就是空间这个东西,你要有k个决策,那么你就要开k+1倍的空间,每一层空间涉及到一个决策,。然后对于第一层的图,还是正常的直接建图,数据怎么搞你就怎么搞。对于第二层及以上的图,将这一层和下一层连一条有向边,表示你这一次的决策
那么通过以上的一些分析,对于一个含n个点的图,我们需要开 n+k * n 的空间,即 n+k * n 个点,举个例子吧,大概就是以下这张图(这个图照搬我同桌的)
具体的实现方法,以例题为例(四倍经验爽不爽,会把四道题都放在下面的)
P4822 冻结
这道题非常模板啊(之后那三道题也非常模板),就是对一个非常正常的图,你需要求一个最短路,但是在你走的时候,你可以对你走的一些边进行一次改变,把这条边的边权改为之前的二分之一,那么这个时候最朴素的想法就是求一个最短路,并且记录这条最短路的边,对这些边排个序,把最长的几条边改了就行了,就有了以下程序(最短路这里就不讲了)
#include
using namespace std;
int n,m,k,u,v,t,tot,ans;
int dis[20010],vis[20010],head[20010];
priority_queue qq;
priority_queue > q;
struct node {
int to,net,val;
} e[20010];
struct nodes {
int id,num;
} pre[20010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline void dijkstra() {
memset(dis,20050206,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty()) {
int x=q.top().second;
q.pop();
if(vis[x]) continue;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
pre[v].id=x;
pre[v].num=e[i].val;
q.push(make_pair(-dis[v],v));
}
}
}
}
int main() {
scanf("%d%d%d",&n,&m,&k);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&t);
add(u,v,t);
add(v,u,t);
}
dijkstra();
int kk=n;
while(kk!=1) {
qq.push(pre[kk].num);
kk=pre[kk].id;
}
while(k--) {
if(qq.empty()) break;
ans+=qq.top()/2;
qq.pop();
}
if(qq.empty()) {
printf("%d",ans);
return 0;
}
while(!qq.empty()) {
ans+=qq.top();
qq.pop();
}
printf("%d",ans);
return 0;
}
那么如果你是这样写的,恭喜你有70分啦,你甚至会发现你连第一个点都是WA,那么举个例子为什么你会错呢?
以下这个图,你跑出来的最短路应该是
1 -> 4 -> 5 -> 3 决策一次之后为18
然而另一条路应该是
1 -> 2 -> 3 决策一次之后为17
那这样你就错辽
那么这样的话,就应该用分层图来做,那么直接看代码
#include
using namespace std;
const int MAXN=1e4+50;
int n,m,k;
int head[MAXN*50],tot;
struct node{
int net,to,w;
}e[MAXN*50];
int d[MAXN*50];
bool v[MAXN*50]; //注意要多开k倍
void add(int u,int v,int w){
e[++tot].to=v;
e[tot].net=head[u];
e[tot].w=w;
head[u]=tot;
} //非常正常地村边
priority_queue< pair > q;
void dij(int s){
fill(d,d+MAXN*50,20040915); //memset只能赋初值为0或-1,其他值应该是fill,不怎么了解的最好就用memset
memset(d,0x3f,sizeof d);
memset(v,false,sizeof v);
d[s]=0;
q.push(make_pair(0,s));
while(!q.empty()){
int x=q.top().second;
q.pop();
if(v[x]==true) continue;
v[x]=true;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
q.push(make_pair(-d[y],y));
}
}
}
} //非常正常的最短路
int main(){
scanf("%d%d%d",&n,&m,&k);
for(register int i=1;i<=m;i++){
int a,b,t;
scanf("%d%d%d",&a,&b,&t);
add(a,b,t);
add(b,a,t); //双向变
for(register int j=1;j<=k;j++){
add(a+j*n,b+j*n,t);
add(b+j*n,a+j*n,t); //在每一层中建一个正常地边
add(a+(j-1)*n,b+j*n,t/2);
add(b+(j-1)*n,a+j*n,t/2); //在下一层连一条单向边,表示你的决策,边权视题目而定
}
}
for(register int i=1;i<=k;i++) add(n+(i-1)*n,n+i*n,0); //终点单独连边
dij(1); //跑最短路
cout< 那么这道题你就成功地A掉了啊,那么接下来就是非常快乐的三倍经验时刻,我会把题目挂在下面(题目不完全相同,但是只是略微区别),然后对于分层图还有另外一种做法,对于空间要求来说更低,蒟蒻暂且不会,之后应该会更吧
P2939 [USACO09FEB]Revamping Trails G
P4568 [JLOI2011]飞行路线
P1948 [USACO08JAN]Telephone Lines S
然后就是 大佬的博客 和 蒟蒻自己的博客