【图论】最短路的传送问题

一.分层图问题（单源传送）

（1）题目

P4568 [JLOI2011] 飞行路线 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

（2）思路

可知背景就是求最短路问题，但难点是可以使一条路距离缩短至0，那如何更好的利用这个机会呢？

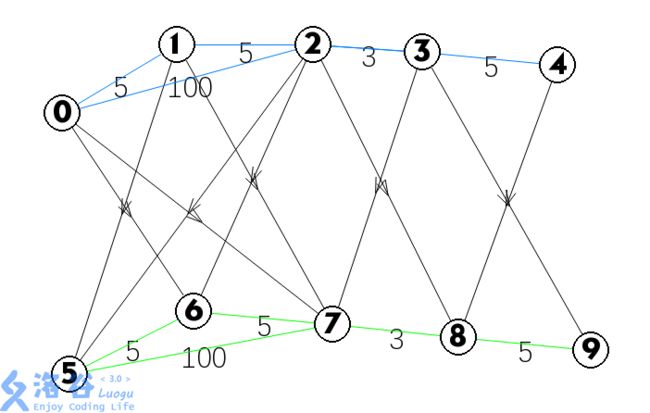
此时我们可以用到分层图，如下：

即我们可以免费往下传一次，其实也就相当于两点距离为0了，这时终点应该9号节点。

于是建图如下：

			add(u+(j-1)*n,v+j*n,0);
			add(v+(j-1)*n,u+j*n,0);
			add(u+j*n,v+j*n,w);
			add(v+j*n,u+j*n,w);

第一个是从上到下，是使用传送的边

第二个是第一个的逆向

第三个是已经用过一次机会，已经在下面了，所以正常边

第四个是第三个的逆向

	for(int j=1;j<=k;j++){
		add(s+(j-1)*n,s+j*n,0);
	}

这个是特殊情况，起点即终点，一路传送，其实多此一举，但没办法，只怪我们把图分层了。不能在自环到达了。

（3）参考代码

#include
using namespace std;
int n,m,k;
int s,e;
struct Edge{
	int u,v,w,next;
}edge[2500001];
int head[110005],cnt;
void add(int u,int v,int w){
	edge[++cnt]=(Edge){u,v,w,head[u]}; head[u]=cnt;
}
int dis[110005],vis[110005];
struct node{
	int u,w;
	bool operator < (const node &x) const{
		return x.wq;
	memset(dis,0x3f,sizeof(dis));
	q.push((node){s,0});
	dis[s]=0;
	while(!q.empty()){
		node temp=q.top(); q.pop();
		int u=temp.u;
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=head[u];i;i=edge[i].next){
			int v=edge[i].v,w=edge[i].w;
			if(dis[v]>dis[u]+w){
				dis[v]=dis[u]+w;
				q.push((node){v,dis[v]});
			}
		}
	}
}
int main(){
	cin>>n>>m>>k>>s>>e;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);add(v,u,w);
		for(int j=1;j<=k;j++){
			add(u+(j-1)*n,v+j*n,0);
			add(v+(j-1)*n,u+j*n,0);
			add(u+j*n,v+j*n,w);
			add(v+j*n,u+j*n,w);
		}
	}
	for(int j=1;j<=k;j++){
		add(s+(j-1)*n,s+j*n,0);
	}
	dijkstra();
	cout<

---

二.多源传送

（1）题目

P6464 [传智杯 #2 决赛] 传送门 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

（2）思路

这题虽然是多源，但只有一个传送门，而且数据范围小，只有100，所以直接上floyd算法！

因为我们不知道传送门怎么建立，所以直接暴力枚举就行了。

我们两重遍历，找出门，在两重暴力folyd即可。

Q：folyd不是三重吗？

A：不是已经知道在哪搭桥了吗？

Q:其他不也可以搭桥吗？

A：前面的预处理三重floyd已经处理好了。

（3）参考代码

#include
using namespace std;
int n,m;
int f[101][101];
int F[101][101];
inline void back()
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			F[i][j]=f[i][j];
}
int main()
{
	scanf("%d%d",&n,&m);
	memset(f,-1,sizeof(f));
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		if(f[u][v]==-1||f[u][v]>w)	f[u][v]=f[v][u]=w;//建边，防重边（不过数据里没有）
	}
	for(int k=1;k<=n;k++)	
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				if(f[i][k]!=-1&&f[k][j]!=-1)
					if(f[i][j]==-1||f[i][j]>f[k][j]+f[i][k])
						f[i][j]=f[i][k]+f[k][j];//Floyd
	int ans=2e9;//较大值
	for(int i=1;i<=n;i++)	
		for(int j=1;j<=n;j++)//暴力枚举
		{
			back();//先让F数组还原成f数组
			F[i][j]=F[j][i]=0;//在教学楼 i 和 j 之间建立传送门
			//i点搭桥 
			for(int x=1;x<=n;x++)	
				for(int y=1;y<=n;y++)	
					if(F[x][y]==-1||F[x][y]>F[x][i]+F[i][y])
						F[x][y]=F[x][i]+F[i][y];//Floyd
			//j点搭桥 
			for(int x=1;x<=n;x++)
				for(int y=1;y<=n;y++)	
					if(F[x][y]==-1||F[x][y]>F[x][j]+F[j][y])
						F[x][y]=F[x][j]+F[j][y];//Floyd
			int res=0;
			for(int x=1;x<=n;x++)	
				for(int y=1;y