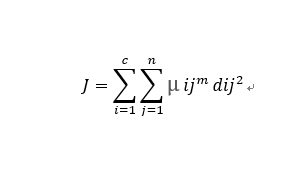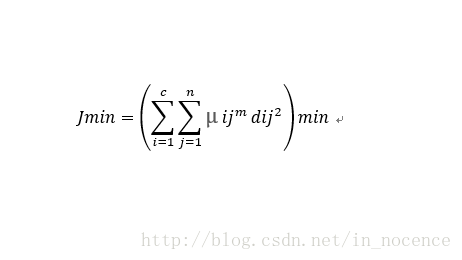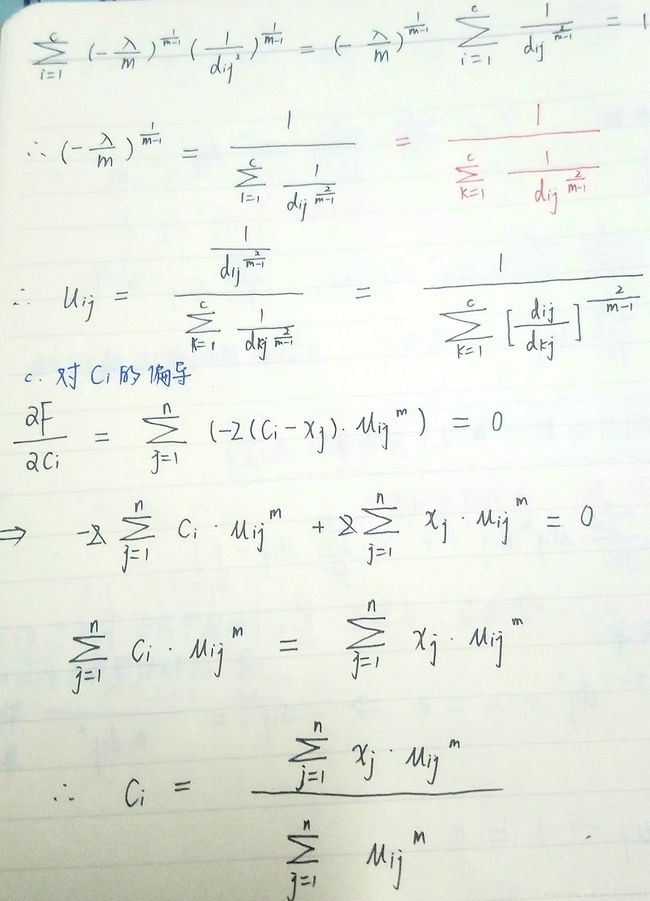FCM聚类算法（模糊C均值算法）

FCM聚类算法(Fuzzy C-Means)

##算法初识

---

FCM算法是一种基于划分的聚类算法，它的思想就是使得被划分到同一簇的对象之间相似度最大，而不同簇之间的相似度最小。模糊C均值算法是普通C均值算法的改进，普通C均值算法对于数据的划分是硬性的，而FCM则是一种柔性的模糊划分。

---

情景：
假设现在有一群人，要将他们自动分成大人和小孩两类，以身高作为分类标准（若身高大于160cm为大人，小于160cm为小孩）。现有一人身高为100cm，那么根据上述标准，不难判断，他会被划分到小孩一组。但是如果他的身高为159cm，该如何划分呢？

IDEA1：无论如何159cm总是小于160cm，应该被分到小孩组。
IDEA2：159cm很接近160cm,更偏离小孩组，应该被分到大人组。

以上两种说法体现了普通C均值算法(HCM)和模糊C均值算法(FCM)的差异：
普通C均值算法在分类时有一个硬性标准，根据该标准进行划分，分类结果非此即彼。（IDEA1）
模糊C均值算法更看重隶属度，即更接近于哪一方，隶属度越高，其相似度越高。（IDEA2）

由以上叙述不难判断，用模糊C均值算法来进行组类划分会使结果更加准确！

---

##清楚概念

大概认识上述二者区别之后，正式了解算法之前，首先分享一些基本概念。

---

迭代

迭代是数值分析中通过从一个初始估计出发寻找一系列近似解来解决问题的过程，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次”迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。在FCM聚类算法中，迭代的目的就是不断优化，使结果无限接近目标函数。

注意：迭代时需要有一个条件来对迭代过程进行控制，保证迭代过程不会无休止的进行。

隶属度函数

隶属度函数是表示一个对象x隶属于集合A的程度的函数，通
常记做μA(x)，其自变量范围是所有可能属于集合A的对象（即集合A所在空间中的所有点），μA(x)的取值范围是[0,1]，即0<= μA(x)<=1。越接近于1表示隶属度越高，反之越低。

模糊集合

一个定义在空间X={x}上的隶属度函数就定义了一个模糊集合A，即这个模糊集合里的元素对某一标准的隶属度是基本相近的。在聚类的问题中，可以把聚类生成的簇看成一个个模糊集合，因此，每个样本点对簇的隶属度就在[0，1]区间内。

聚类中心

经过查阅以往论文以及相关资料，我对聚类中心的理解大概就是“分类标准”这样一个概念。
聚类中心的选取大致有两种方式：

1…典型的做法是从所有数据点中任取任取c个点作为聚类中心，选点前提是要使价值函数（目标函数）达到最小。—>价值函数下面会具体讲。

2…每次选簇的均值作为新的中心，迭代直到簇中的对象的分布不再变化。其缺点是对于离群点比较敏感，因为一个具有很大或者很小极端值的对象会对数据分布产生较大的影响。

相似度算法—>欧几里德距离

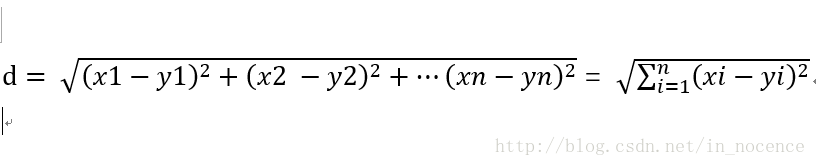
欧氏距离越小，相似度就越大，欧氏距离越大，相似度就越小。结合以上隶属度的概念，我们将将相似度与1作类比，同样，相似度数值越接近于1，表示相似度越高，反之则低。

价值函数（目标函数）

目标函数本质上是各个点到各个类的欧式距离的和。
目标函数可通过隶属度一级样本x到聚类中心的距离这两个量来直观表示（其中μij是隶属度，dij是样本到聚类中心的距离）：

该算法中的c表示聚类数目，假设有n个样本数据xj(1,2,…,j)，每个数据有s个特征，将这n个数据分成c组，算法输出一个c行n列的矩阵U（注意区分：（2）（3）式中的Uij表示的不是矩阵，而是）。求每组的聚类中心ci，使得目标函数最小（因为目标函数与欧几里德距离有关，目标函数达到最小时，欧式距离最短，相似度最高），这保证了组内相似度最高，组间相似度最低的聚类原则。

根据以上叙述以及式（2），我们可得最优解的表达式是：

加权指数m

m实质是一个刻画模糊化程度的参数（m>1），当m=1时模糊聚类就退化为HCM，研究表明m的最佳选择范围为[1,2.5]，一般m取2为宜。

##函数求解

关于目标函数的最优解，这就是考验数学的时候哇……绝望.jpg

由于对图片公式加序号太麻烦，为表达方便，这里特新列一张公式表。

##算法过程

初始化：取模糊加权指数m=2,设定聚类数目c,设定迭代停止的阈值ε，一般ε取0.001，初始聚类中心值ci(i =0,1,2….c),设置迭代计数器T = 0,最大迭代次数T = max.

步骤1：用值在0，1间的随机数初始化隶属矩阵U，使其满足式（1）中的约束条件。

步骤2：用式（3） 计算c个聚类中心ci（i=1,…,c）。

步骤3：根据式（2）计算价值函数。如果它小于某个确定的值，或它相对上次价值函数值的改变量小于某个阀值ε，则算法停止。

步骤4：用式（4）计算新的U矩阵。返回步骤2。

上述算法也可以先初始化聚类中心，然后再执行迭代过程。由于算法的性能依赖于初始聚类中心。因此，我们要么用另外的快速算法来确定初始聚类中心，要么每次用不同的初始聚类中心启动该算法，多次运行FCM，使结果不断接近目标函数。

##心得总结

FCM与普通分类的区别就在于FCM用模糊划分，使得每个给定数据点用值域在0到1之间的隶属度函数确定其属于各个类的程度以达到分类的目的。