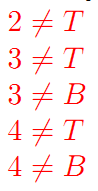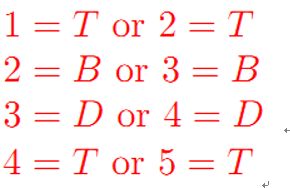人工智能学习笔记(二)---博弈&约束满足问题&逻辑与推理
目录
一、博弈
极大极小算法
α-β剪枝
例题:
二、约束满足问题
定义:
约束传播
回溯搜索与启发式(略)
例题:
三、逻辑与推理
一、博弈
(a)什么是博弈问题,它和其他搜索方法比较有什么特点?
(b)提高博弈问题的搜索效率有什么方法并分析每种方法对算法最优性的影响。
[answer]:
(a)有完整信息的、确定的、轮流行动的、两个以上Agent的对抗搜索问题。与其他搜索算法相比,它主要的特点是多agent和更加注重实时性。
(b)提高博弈问题搜索算法效率的方法:
(1)α-β剪枝,不影响算法的最优性
(2)采用评估函数(评估当前位置的有效性)和截断测试(限制深度/时间)的方式,影响算法的最优性
(3)向前剪枝策略只考虑最优的部分分支,影响算法的最优性
(4)采用搜索表的方式,不影响算法的最优性
极大极小算法
max nodes:己方的选择结点,会选择评估值最大的子结点
min nodes: 对方的选择结点,会选择评估值最小的子结点
MINIMAX:所谓的极小极大值,对于MAX NODES它的值为子结点中的最大效用值,对于MIN NODES它的值为子结点中的最小效用值。
首先搜索到低层叶结点并获取其效用值,然后将极小极大值回传给上一层结点,直到值回传给根结点。
该算法对博弈树进行完整的深度优先搜索,如果树的最大深度是m,在每个结点的行棋有b个,那么时间复杂度为O(b^m)
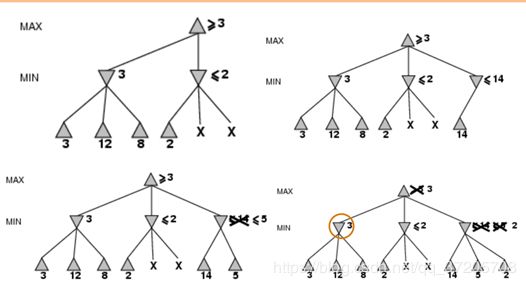
α-β剪枝
α-β剪枝其实就是在极小极大搜索的基础上做了剪枝处理(没有搜索完整棵树)
对每个结点取得的α和β
如果α<=N<=β则该结点可取,否则舍弃该结点
MAXNODE向上传递β,MINNODE向上传递α
QUESTION:这两个参数是否为全局变量,或者每个结点维护一组?---应该是每个结点自行维护
α = 到目前为止路径上发现的MAX的最佳(即极大值)选择
β = 到目前为止路径上发现的MIN的最佳(即最小值)选择
例题:
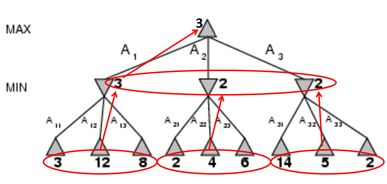
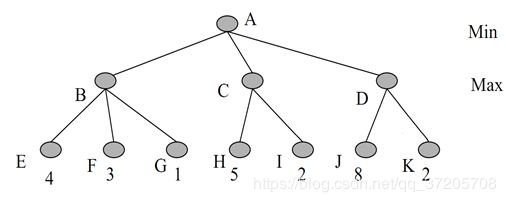
考虑下图的极大极小值树,搜索顺序从左到右。
a) 根据极大极小值算法给出A结点的值并给出决策路径。
A:4; A-B-E
b) 根据剪枝算法给出被剪枝的部分。
I, K
c) 如果搜索顺序改为从右到左,被剪枝的部分还是一样吗?如果不是,给出被剪枝的部分。
不一样,没有结点被剪枝
d) 如果B,C,D结点都变为Chance结点,其子节点出现的概率均等,计算A结点的值。
B=(4+3+1)/3=8/3
C=(5+2)/2=7/2
D=(8+2)/2=5
A=min(8/3,7/2,5)=8/3
二、约束满足问题
定义:
约束满足问题(Constraint satisfaction problem)是一类数学问题,它的定义为一组状态必须满足于若干约束或限制的对象(object)。 CSP表示的是问题中的实体,有限数量、同类型的约束加之于变量之上, 这类问题通过约束满足方法解决。CSP是人工智能和运筹学的热门主题, 这是因为它们公式中的规律提供了一个分析和解决很多不相关问题的共同基础。 CSP通常表现出高复杂性, 需要结合启发式搜索和联合搜索方法来在合理的时间内解决问题。
将一个问题建模为CSP问题需要对其形式化。简而言之,CSP的策略缩小了搜索空间也加快了搜索速度。
形式化:
X、D、C
X:变量集合
D:值域集合 每个变量都有自己的值域
C:约束条件集合
一元约束:只限制单个变量的取值
二元约束:与两个变量有关…
全局约束:变量个数任意,如Alldiff。
定义状态空间:
完整赋值:每个变量都已赋值
部分赋值:只有部分变量赋值
绝对约束->偏好约束->求最优解的问题->约束优化问题(COP)
约束传播
核心思想:局部相容性。CSP中除了搜索(从几种可能性中选择新的变量赋值)外,还可以进行一种称为约束传播的特殊推理—即使用约束来减小一个变量的合法取值范围。(可以称之为搜索预处理)
相关定义:把变量看作图中的结点,约束为图中的弧。
局部相容性的分类
结点相容:单个变量(对应一个节点)值域中的所有取值满足它的一元约束,就是节点相容的。
弧相容:如果CSP中某变量值域中所有取值满足该变量所有二元约束,则此变量弧相容
如果每个变量相对其他变量都是弧相容的,则称该网络是弧相容的。
AC-3算法
应用了AC-3后,要么每条弧都是弧相容的,要么有变量的值域为空,后者说明CSP无解。
路径相容:弧相容可能缩小变量的值域,有时甚至还能找到解(每各变量值域大小都为1时),或者有时发现CSP无解(一些变量的值域大小=0)。
但是弧相容也会失败(比如澳大利亚地图着色问题,如果只有两种颜色,弧相容意义不大),所以才要用更强的相容概念。
路径相容---观察变量得到隐式约束,并以此来加强二元约束。
k-相容:如果对于任何k-1个变量的相容赋值,第k个变量总能被赋予一个和前k-1个变量相容的值,那么这个CSP就是k相容的
回溯搜索与启发式(略)
推理和搜索交叉进行
最少剩余值和度启发式
最少约束值启发式
冲突引导的回调
例题:
你是一个正在抓捕毒贩(D)的侦探,有证据显示一个或者多个毒贩藏匿在一个小公寓内,公寓总共有5间房,每间房里面可能藏匿了毒贩,但也可能是无辜的人,包括:成年人(A),带有婴儿的家庭(B),年轻人(T)。你如果想破门而入需要绝对确认毒贩在里面,否则你可能会受到擅入民居的指控。
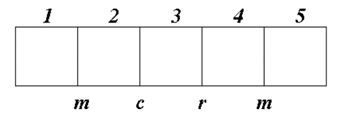
为了帮助你缩小搜索范围,你可以走到两个房间的中间位置,然后听到两个房间里发出的声音的最大值。已知年轻人听音乐的声音最大(m),其次是小孩的哭声(c),再者是毒贩发出的沙沙声(r),最安静的是成年人(s)。比如说,如果两个相邻房间一个是婴儿,一个是年轻人,那么你站在中间只能听到音乐声。图二展示了站在房间中间听到的声音,请回答如下问题:
图二:房间声音分布图
a)给出该CSP问题的变量和值域
变量:1,2,3,4,5五个房间
值域:{A,B,D,T}四种人
b)根据图二的声音分布给出该问题的一阶约束和二阶约束内容(6分);
一阶: 二阶:
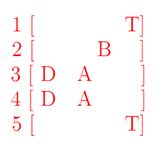
c)根据弧一致性对所有的变量进行值域缩小并给出缩小的结果
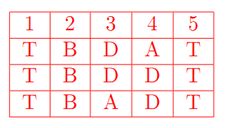
d)给出该CSP问题的所有解
e)你是否可以破门进入房间4?给出你的理由
不可以, 因为房间4里可能是成年人
三、逻辑与推理
基本概念
KB:知识库,知识库是一个语句集合,这些语句用知识表示语言表达,表示了关于世界的某些断言。当某些语句是直接给定而不是推导的时候,将其称为公理。
将新语句添加到知识库以及查询目前所直内容的方法分别是TELL 和 ASK , 这两个任务都涉及到推理。
每次调用逻辑Agent程序它都做三件事
①TELL 知识库它感知到的内容
②ASK 知识库应该直行什么行动 (这一步需要大量的推理)
③Agent程序用TELL告诉知识库它所选择的行动,并执行该行动
一阶逻辑
一阶逻辑,即更加形式仔细的描述“命题逻辑”的一种方式,通过引入“量词”“个体词”和“谓词”三个概念来解决“命题逻辑”对一些命题表达的局限性问题。
1.个体词:可指独立存在的客体,可以是一个具体事物,也可以是一个抽象的概念。
①个体常项:表示具体的或特定的个体的词。常用小写字母a,b,c,d……表示。
②个体变项:表示抽象的,或泛指的个体词。常用x,y,z……表示。
③个体域:个体变项的取值范围。可以是有限的集合,也可以是无限的集合。
2.谓词:用来描述个体词的性质或个体词之间关系的词。
①谓词常项:称表示具体性质或关系的谓词。用大写字母F,G,H……表示。
②谓词变项:表示抽象的或泛指的谓词。也用F,G,H……表示。
③元数:谓词中包含的个体词数。
④零元谓词:不带个体变项的谓词。
3.量词:表示数量的词。
全称量词:“一切,所有,任意的……”等词用 ∀表示。∀x表示对个体域里的所有个体, ∀xF(x)表示个体域里的所有个体都有性质F。
特称量词:“存在着,至少有一个……”等词用∃表示。∃x,∃xF(x)同上。
一阶逻辑转换为CNF范式(合取范式)的步骤(CNF一阶逻辑的CNF范式不包括量词!)
①消除蕴含词(即箭头,注意加否定的位置!一般是在量词之后,如果前面全部被一个括号包住则否定在最前面(所有的量词之前))
②否定内移,包括量词的否定转换
③变量标准化,即使用相同变量名的语句(但实际上不是同一变量的)改变其中一个变量的名字
⑤删除全称量词,这个一般可以直接删除(变量保持不变)
⑥分配律…
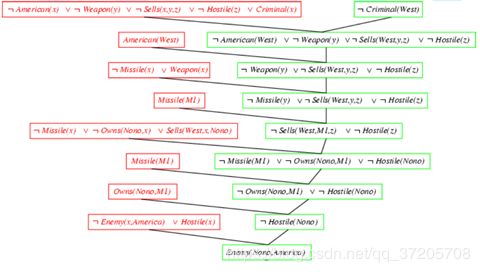
归结算法:
归结:所谓归结即![]() (互补文字)
(互补文字)
归结规则的输入要求是合取范式(CNF)
为了证明KB|=α,需要证明 KB∧¬α 是不可满足的(反证)
步骤:①把 KB∧¬α转化为CNF
②对结果子句运用归结规则,对含有互补文字的子句进行归结产生新子句,如果该新子句尚未出现过,则将它加入子句集中。此过程一直持续,直到以下两件事情之一发生
---没有可以添加的新语句,这种情况下,要推理出的结论是错误的
---两个子句归结出空子句,这种情况下,要推理出的结论是正确的(因为是反证)
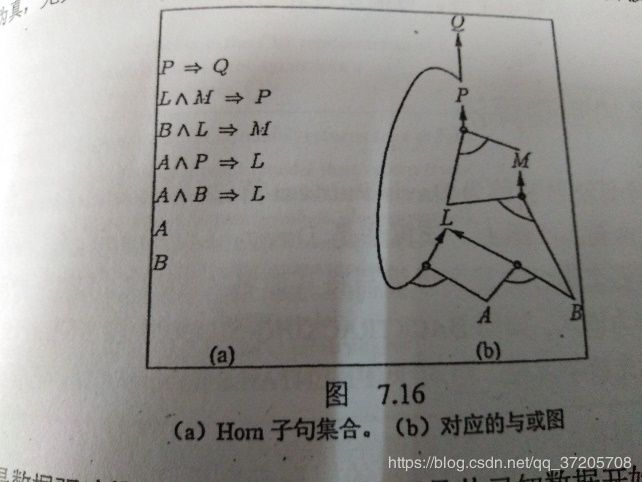
前向链接与反向链接
前向连接算法:
目标:判定单个命题词q是否被限定子句的知识库所蕴涵
过程:从知识库的已知事实(正文字)出发,如果蕴含式的所有前提已知,那么就把它的结论添加到事实集。这一过程持续进行直到查询q被添加或无法进行更进一步的推理。(上图查询Q)
分析:前向链接是数据驱动推理的实例---即推理是从已知数据开始的,但是有可能推导出大量的无关的结果。
反向链接:反向链接从查询开始推理,如果查询q已知为真则无须进行任何操作,否则算法寻找知识库中以q为结论的蕴含式,如果其中某个蕴含式的所有前提都能证明为真,则q为真。反向链接是一种目标制导的推理形式。(在上图中相当于沿着Q后退)
例题
把下列表达式转换为CNF形式
Answer:
![]()
其中,C1,C2是常数,z,w是变量,F()表示函数,符号表示可以不一样。