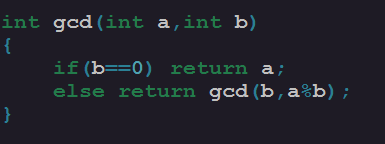
求最大公因子（辗转相除法原理）（扩展的欧几里德算法）

    while(n != 0)
    {
        r = m % n;
        m = n;
        n = r;
    }
    printf("Their greatest common divisor is %d.\n", m);

都知道在求最大公因子（最大公约数）的时候，使用欧几里得算法（辗转相除法）。下面来研究这个算法怎么推论出来的。

首先看：

我们用 b|a 表示b整除a。也称b是a的因子。

用gcd（a，b）表示a和b的最大公因子。

如果 b|g 且 b|h，则对任意的整数m和n，有 b|(mg+nh)。

 

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------

下面推论：

假设我们有整数a，b使得d = gcd（a，b）。

根据除法，我们知道

a =q₁b + r₁            0 <= r₁ < b

_{所以由 d | a 和 d | b 可以推出}

d | (ma+nb)   ----->   d | (a - q₁b )     --------->  d | r₁

现在我们知道 d | b 和 d | r₁

假设有任意的整数 c 整除 b 和 r_{1，则有c | (mb+nr1)，所以有c | (q1b+r1)  ------>  c | a}

因为 c 能同时整除 a 和 b，必须有 c <= d，而d 是 a和b的最大公因子。

因此，

d = gcd（b，r₁）

如此循环，直到 r_i = 0。

=================================================================================================================

欧几里德定理： gcd(a, b) = gcd(b , a mod b)

=================================================================================================================

扩展的欧几里德：

知道了 a 和 b 的最大公约数是 d ，那么，我们一定能够找到这样的 x 和 y ，使得: 

ax + by = d = gcd(a，b)

 我们观察到：欧几里德算法停止的状态是： a= gcd ， b = 0 ，

    当然这是最终状态，但是我们是否可以从最终状态反推到最初的状态呢？

    假设当前我们要处理的是求出 a 和 b的最大公约数，并求出 x 和 y 使得 a*x + b*y= gcd ，而我们已经求出了下一个状态：b 和 a%b 的最大公约数，并且求出了一组x1 和y1 使得： b*x1 + (a%b)*y1 = gcd ， 那么这两个相邻的状态之间是否存在一种关系呢？

    我们知道：

a%b = a - (a/b)*b

（这里的 “/” 指的是整除，例如 5/2=2 , 1/3=0），那么，我们可以进一步得到：

        gcd = b*x1 + (a-(a/b)*b)*y1

            = b*x1 + a*y1 – (a/b)*b*y1

            = a*y1 + b*(x1 – a/b*y1)

    对比之前我们的状态：求一组 x 和 y 使得：a*x + b*y = gcd ，是否发现了什么？

    这里：

        x = y1

        y = x1 – a/b*y1

以上就是扩展欧几里德算法的全部过程，依然用递归写：

应用在乘法逆元：