2018美赛B题总结
Update 2019/07/26:根据读者提出的问题,添加了查找数据方法、时间安排、论文及代码的下载地址等内容。
前言
本文主要是记录这次建模的过程和思路。用到的模型简单提及,并省略数据和结论。
涉及到的最小二乘法、模糊数学模型和马尔科夫链知识可以见我的文章“半小时学习最小二乘法”“模糊评价模型-以2018美赛为例”“马尔科夫链详解(TBC)”。
这里是我的个人网站:https://endlesslethe.com/2018-mcm-summary-of-b.html 有更多总结分享,最新更新也只会发布在我的个人网站上。排版也可能会更好看一点=v=
问题
Problem: A large multinational service company, with offices in New York City in the United States and Shanghai in China, is continuing to expand to become truly international. This company is investigating opening additional international offices and desires to have the employees of each office speak both in English and one or more additional languages. The Chief Operating Officer of the company has hired your team to investigate trends of global languages and location options for new offices.
Part I:
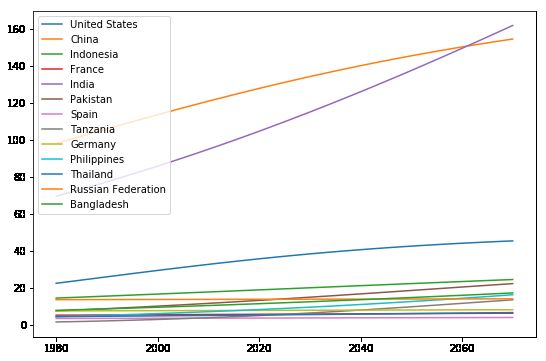
A. Consider the influences and factors described in the background paragraph above, as well as other factors your group may identify. Based on projected trends, and some or all of these influences and factors, model the distribution of various language speakers over time.
B. Use your model to predict what will happen to the numbers of native speakers and total language speakers in the next 50 years. Do you predict that any of the languages in the current top-ten lists (either native speakers or total speakers) will be replaced by another language? Explain.
C. Given the global population and human migration patterns predicted for the next 50 years, do the geographic distributions of these languages change over this same period of time? If so, describe the change.
Part II:
A. Based on your modeling from Part I, and assuming your client company wants to open six new international offices, where might you locate these offices and what languages would be spoken in the offices? Would your recommendations be different in the short term versus the long term? Explain your choices.
B. Considering the changing nature of global communications, and in an effort to save your client company resources, might you suggest that the company open less than six international offices? Indicate what additional information you would need and describe how you would analyze this option in order to advise your client.
读题
这个问题分为两部分(Part),第一部分要求解决“建立语言使用人数的分布模型”“根据模型预测50年后的使用top10”“预测50年后各语言的地理分布”三个问题。
对于这三个问题,我的理解重点放在A的“分布模型”和C的“地理分布”这里:
- “分布模型”应该指的是某种语言使用人数的模型,A问题的目的就是先对各种语言人数建立一个整体模型。
- B问题根据A建立的问题不难解决。
- 而“地理分布”指的是某一种语言在其他国家的分布模型,C的目的是将整体模型细化,讨论某种语言在不同国家人数的分布情况。
第二部分要求解决“六个国际办公室的选址,并分短期和长期两种”“能否增减办公室数量?(如果有你需要的一些额外的信息,你会如何分析)”两个问题。
问题A可以结合语言趋势和经济、基础建设这些影响因素来确定。短期就根据当前的数据,长期就根据最近10年的增长趋势。(显然,这不应该是一个图论题。)
问题B是一个开放性的题。可以从收益和成本来讨论。
总体来看,第一部分和第二部分相对独立,可以先对前面的第一部分建模。
第一部分ABC
因为在建模开始前,我一直在看智能算法和随机采样,所以看到题目的第一反应就是用马尔科夫链。也是因为这个原因,所以我们队在选题上面花的时间并不多,第一天上午大致看了一下其他题,就确定做B了。
这里我直接给出第一部分建模的最终模型了:
[外链图片转存失败(img-Kil9Pyz6-1564162600180)(https://endlesslethe.com/wordpress/wp-content/uploads/2018/04/总体模型.bmp)]
总体模型
- 先将语言人数分为母语和第二语言。
- 其中,母语可以通过人口增长模型描述。
- 第二语言的人数比例通过马尔科夫链的状态转移矩阵描述,通过各种语言多年第二语言的使用人数,估计出各语言的转移趋势。
a. 建立马尔科夫链模型
b. 最小二乘法计算转移矩阵
c. 估计50年后的情况
而马尔科夫链的好处是直接解决了ABC三个问题,不存在细化模型的烦恼了。
语言人数模型
对于第j种语言,其使用人数等于母语人数+第二语言人数。
\[{N^{[j]}} = N_{native}^{[j]} + N_{second}^{[j]}\]
\(N_{native}^{[j]}\)=一个国家的人口数+出生人口-死亡人口-净移民
\(N_{second}^{[j]}\) =所有国家第j种第二语言总人数+新学习人数-死亡人数
即
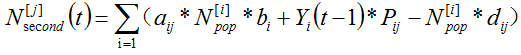
Where aij denote the probability of new birth in the i-th country learning the j-th language as second language, dij denote the death rate of the j-th country using the i-th language as second language, bi denote the birth rate of the i-th country, N[i]pop denote the population of the i-th country.
这里有几点假设简化:
\(N_{native}^{[j]}\)=一个国家的人口数
\[N_{second}^{[j]} = \mathop \sum \limits_{i = 1}^n {Y_i}\left( {t - 1} \right) * {P_{ij}}\]
人口模型
显然,母语人数可以使用Logistic人口增长模型来描述。
这里我直接给出公式,具体可由微分方程推导:
\[x\left( t \right) = \frac{{{x_m}}}{{1 + (\frac{{{x_m}}}{{{x_0}}} - 1){e^{ - rt}}}}\]
其中\(x_m\)是环境容纳量,\(r\) 是人口增长率. \(x(t)\) denote the \(N^{[j]}_{native}\) of big nations. \(x_0\) denote the time point we choose to start predicting. \(t\) denote the years between the year which we choose to start and which we predict.
\(r\)可以通过世界银行的各国人口增长率数据得到。\(x_m\)严谨一点可以通过方程拟合。但因为不是重点,自己估计也行,就是每一个国家能最多容纳多少人(环境容纳量),看最后曲线是否和历史基本吻合。
使用马尔可夫链预测第二语言迁移情况
我们可以发现第二语言的人数比例可以通过马尔科夫链的状态转移矩阵描述,从而通过各种语言多年后第二语言的使用人数,估计出各语言的转移趋势。
设第\(j\)种第二语言在第\(t\)年的使用人数为\(Y_j(t), j=1,2,3\)。
从第i种第二语言转而使用第\(j\)种作为第二语言的概率为\(P_{ij}, i, j=1,2,3\)
记国家总数为\(n\),我们使用的样本数为\(t\),即14-16年的4年数据
所以状态转移概率矩阵为:
\[{\rm{P}} = {\left( {\begin{array}{*{20}{c}}
{{P_{1,1}}}& \cdots &{{P_{1,n}}}\\
\vdots & \ddots & \vdots \\
{{P_{n,1}}}& \cdots &{{P_{n,n}}}
\end{array}} \right)_{n \times n}}\]
马尔科夫预测模型为:
\[Y_2=Y_1 P\]
其中
\[{Y_1} = {\left( {\begin{array}{*{20}{c}}
{{Y_1}\left( 0 \right)}& \cdots &{{Y_n}\left( 0 \right)}\\
\vdots & \ddots & \vdots \\
{{Y_1}\left( {t - 1} \right)}& \cdots &{{Y_n}\left( {t - 1} \right)}
\end{array}} \right)_{t \times n}}\]
\[{Y_2} = {\left( {\begin{array}{*{20}{c}}
{{Y_1}\left( 1 \right)}& \cdots &{{Y_n}\left( 1 \right)}\\
\vdots & \ddots & \vdots \\
{{Y_1}\left( t \right)}& \cdots &{{Y_n}\left( t \right)}
\end{array}} \right)_{t \times n}}\]
由最小二乘法可知,结果可以写为:\[P = {\left( {{Y_1}^T{Y_1}} \right)^{ - 1}}{Y_1}^T{Y_2}\]
这样我们通过各种语言多年第二语言的使用人数,估计出各语言的转移趋势。
关于最小二乘法可以见我的文章《半小时学习最小二乘法》(https://endlesslethe.com/easy-to-learn-ols.html )
马尔科夫链的平稳性保证
在比赛时我是觉得这就是一个多元回归方程组而已,查了查中文文献,发现国内都用的最小二乘,就直接用最小二乘法来计算了。
但这里有一个问题没有解决:如何保证计算得到的矩阵是随机矩阵?也就是说如何满足Pij都为正,且每一行的和为1呢?如果不满足这个条件的话,若干年后可能不是平稳分布。
我在谷歌上搜了一下,有挺多相关论文的,发表时间从1970到2017都有。感兴趣的可以看一下,我不打算细看了,下次用到的时候再看吧。
- A Formula for the Powers of the Transition Matrix
- Estimation in Markov Models from Aggregate Data
- A REVIEW OF THE ESTIMATION OF TRANSITION PROBABILITIES IN MARKOV CHAINS
- Efficient Estimation of Transition Probabilities in a Markov Chain
- Improving the Estimation of Markov Transition Probabilities Using Mechanistic-Empirical Models
结果
第二语言比例:(数据太少,而且历年第二语言统计数据变化不大,我感觉是统计机构把往年数据当做新的用的原因)
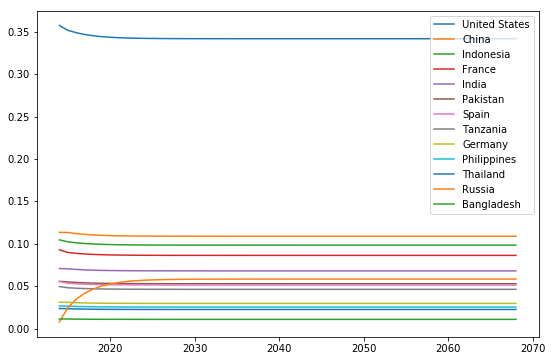
问题C:是问地理分布,显然指的是第二语言而不是母语。我用百度ECharts的js库做个各国的地理分布情况,然后ps到一张图上。
[外链图片转存失败(img-M8Y6gWjV-1564162600181)(https://endlesslethe.com/wordpress/wp-content/uploads/2018/04/NeoImage_副本.jpg)]
第二部分A
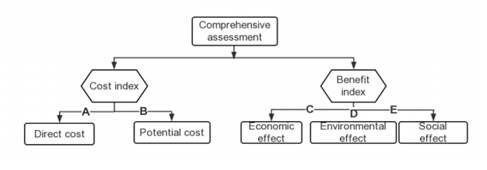
因为这是个多因素、决策性问题,所以我使用的是模糊数学+层次分析(Fuzzy Mathematical Model+AHP)。其实单纯使用AHP也行,但是听说不建议将AHP作为主模型,模糊数学还和数学沾点边,所以使用的是两者结合。
这部分的细节可以见“模糊评价模型-以2018美赛为例”
分为以下六步:
- 为每个属性确定隶属函数
- 根据数据计算隶属度
- 确定评价矩阵,计算权重
- 检验评价矩阵
- 计算最后得分并排序
- 选取前6个
隶属函数
根据预估的评价函数形状确定评价函数(隶属函数)
- 语言趋势
\[y = \left\{ \begin{gathered}
\frac{{10x}}{{{x_{\max }}}}if(x < 0.1{x_{max}}) \hfill \\
0if(x < 0) \hfill \\
1else \hfill \\
\end{gathered} \right.\] - 人均GDP \[y = \left\{ {\begin{array}{*{20}{c}}
{0if(x < 0.5\bar x)} \\
{\frac{{x - 0.5\bar x}}{{2.5\bar x}}else} \\
{1if(x > 4\bar x)}
\end{array}} \right.\] - 文化软实力 \[y = \frac{x}{{{x_{max}}}}\]
- 基础设施 \[y=x^2\]
评价矩阵
第二部分B
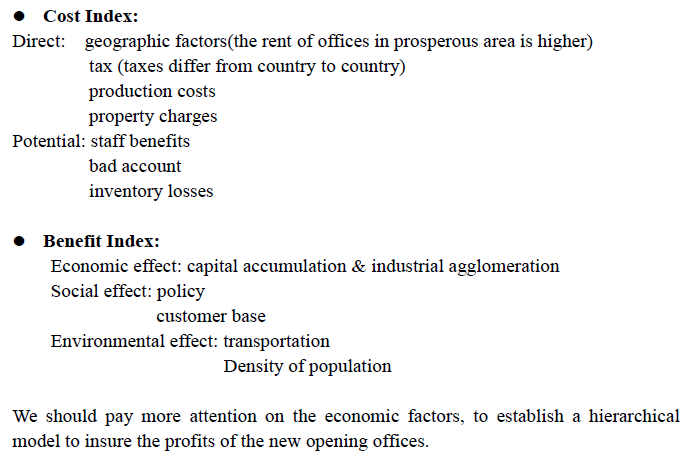
本来问题就很宽泛,定性地谈论一下收益和成本即可。
我的感受与建议
这次一个人完成建模、推导、找数据、计算、检验、作图整个流程,甚至写了一点论文_(:з」∠)_
感谢队友的陪伴,做出结果的时候确实很开心。
但有一点小遗憾:因为个人精力有限,很多有趣的部分都没有深入讨论,而是当做假设忽略。最后的模型有些粗糙。
最后得了M奖还挺意外的,总的看来,都没用什么复杂的方法,最后所有代码也不过800+行,智能算法和机器学习方法都没有用上。
优点是建模思路还算全面,流程也没有遗漏。论文队友确实花了挺大力气,结构比较完整、规范。
建议
- 在建模过程中三个人要能一起现场讨论。这是最基本的
- 在比赛开始前最好能有一次模拟赛。可以明确分工,并发现word经常排版错误等意外情况
- 最好使用Latex。但如果之前没有用过Latex,要么放弃,要么用一场模拟赛来减少意外情况
- 做好心理准备。虽然通常是一个编程、一个设计模型、一个写论文的,但是世界上总是有种种意外对吧。。。
- 负责论文的同学尽量多看往年论文,结构写好
- 图片尽量弄好看一点
- 解法不要求无懈可击,有想法,能得出结论就好
- 如何得到数据这个问题非常关键,数据的有无和质量影响极大
时间安排
Day1 我们第一天早上确定的马尔科夫链模型(因为我对马尔科夫链比较熟悉,基本看到题目就确定思路了),下午便开始找数据和完善细节
Day2、3 包括找数据和处理数据(处理数据非常花时间)弄到第二天晚上都还剩一点,队友也做了一部分。在去吃饭和睡觉的路上,告诉队友思路,同时完善细节,队友根据思路开始写论文。
Day4 有了数据,其实计算结果很简单,因为用到都是基础的数学模型,大概花了一天多一点的时间(包括把整个模型用中文整理出来,交给负责写论文的队友)。
Day5 最后一天下午和晚上完成结果的检验,并制作好简洁、美观的图表,以便队友完成论文的编写
因为这次主要是数学模型,所以写代码花费时间不是很多,反而在数据处理上花了大量时间。神经网络同理,代码量也不是很大,却很需要数据(数学建模的数据量都不太适合用神经网络)。但如果是个模拟类的(比如高速公路行驶规则设计)问题,就不太需要数据了,主要靠编写代码进行模拟。
数据、论文和代码
数据
官方给了wiki链接,但只有当年的第二语言人数。So:
- 通过查阅wiki历年的版本,可以得到部分年份的数据
- 有一个大概叫《世界语言杂志》的期刊,它当时在网上提供了部分年份的数据
对于第二部分人均GDP、文化软实力等可以查阅世界银行的数据库。
PS:我觉得查找数据的能力对美赛影响挺大的,大家还是要善用搜索引擎,特别是google。在开赛前也最好加入几个美赛群,看看有没有资料分享(平均水平较低,平均进度慢,不要被影响了)。
论文
我们的论文未必写得很好,但结构是完整规范的,该有的部分都有。
至于内容,其实我在提交前都没有看过,都是我口述后队友完成的。所以就建模流程而言,有的地方逻辑顺序有错误,整体思路参照我的这篇文章。
下载地址:https://endlesslethe.com/wordpress/wp-content/uploads/2018/06/MCM-B-91973.pdf
代码
下载地址:https://github.com/EndlessLethe/ProblemsAndCode/blob/master/2018mcm%20b.ipynb