毕业设计实用模型(二)——时间序列之SARIMA
时间序列之SARIMA
- 00引言
- 1、三种模型的区别
- 2、数据模拟
- 2.1arma
- 2.2arima
- 2.3sarima
- 3、总结
- 4、参考文献
00引言
在毕业实用统计模型(一)——时间序列1中,介绍了一般的时间序列的建模思路,主要介绍ARMA模型以及R语言的实现。然而在实际还会遇到一些其他的模型ARIMA、SARIMA。而模型参数也会也会变的复杂,从pq到pdq到pdqPDQS。本文主要通过R语言生成符合三种模型的随机数,进行建模预测。给大家看一下如何操作。
在写模型之前先给大家介绍一个时间序列总结的不错的链接2(见参考文献[2])。
1、三种模型的区别
下面表格中给出常见的时间序列模型。
| 模型 | 适用数据 | 参数 |
|---|---|---|
| ar | 自回归模型(平稳数据) | p |
| ma | 滑动平均模型(平稳数据) | q |
| arma | 自回归滑动平均模型(平稳数据) | (p,q) |
| arima | 加入了差分(带有趋势的不平稳数据) | (p,d,q) |
| sarima | 加入了季节因素(带有趋势周期的不平稳数据) | (p,d,q)(P,D,Q)[s] |
2、数据模拟
此部分使用数据模拟的方式分别建立上述三种模型。下面是运行代码所需要的包,自行安装载入。
# 载入所需包
library(tseries)
library(zoo)
library(forecast)
2.1arma
# 构造数据
> ts1 <- arima.sim(n = 100,list(ar = c(0.8, -0.5), ma = c(0.2, 0.5)))
# 建模
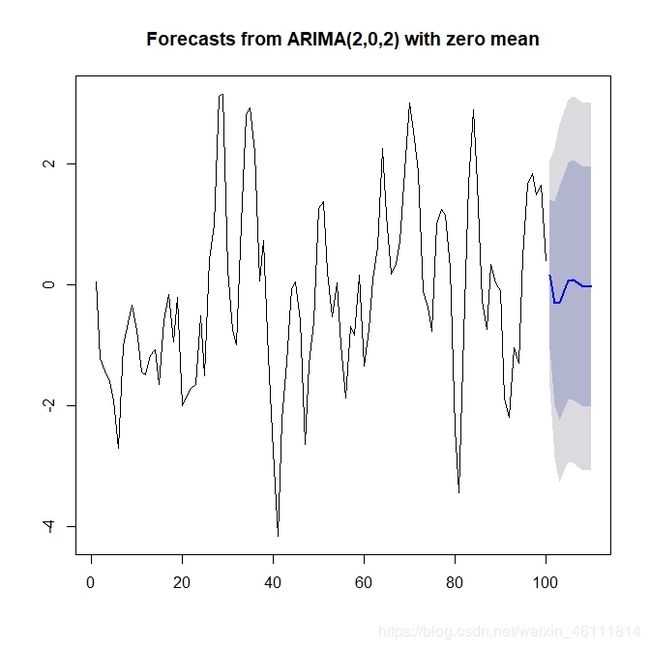
> (fit <- auto.arima(ts1, ic = "aic"))
Series: ts1
ARIMA(2,0,2) with zero mean
Coefficients:
ar1 ar2 ma1 ma2
0.7477 -0.4414 0.1682 0.5319
s.e. 0.1611 0.1354 0.1471 0.1227
sigma^2 estimated as 0.9337: log likelihood=-137.19
AIC=284.37 AICc=285.01 BIC=297.4
> x.fore <- forecast(fit, h = 10)
> plot(x.fore)
2.2arima
先看固定的趋势:
> (fit <- auto.arima((1:100)^2, ic = "aic"))
Series: (1:100)^2
ARIMA(0,2,0)
sigma^2 estimated as 4: log likelihood=-206.98
AIC=415.97 AICc=416.01 BIC=418.55
> x.fore <- forecast(fit, h = 10)
> plot(x.fore)
效果:
再看一下函数filter和数据presidents构造的时间序列。
> ts2 <- filter(presidents, rep(1, 3))
> plot.ts(ts2)
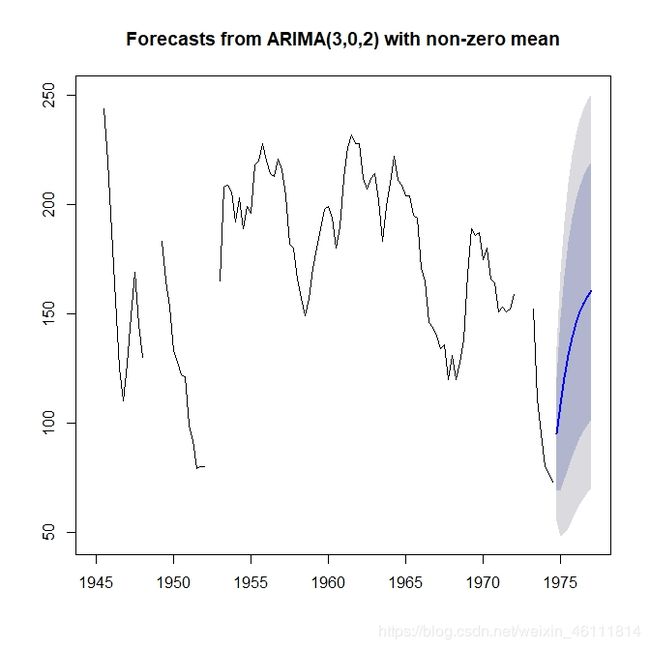
> (fit <- auto.arima(ts2, ic = "aic"))
Series: ts2
ARIMA(3,0,2) with non-zero mean
Coefficients:
ar1 ar2 ar3 ma1 ma2 mean
0.6180 0.4213 -0.2307 1.1205 0.9496 169.2646
s.e. 0.1051 0.1156 0.1039 0.0700 0.0672 13.2637
sigma^2 estimated as 91.77: log likelihood=-400.08
AIC=814.15 AICc=815.18 BIC=833.49
> x.fore <- forecast(fit, h = 10)
> plot(x.fore)
2.3sarima
这里在加入季节因素,注意数据的构造,如果不用ts函数包装则不能建立此模型。
先构造数据
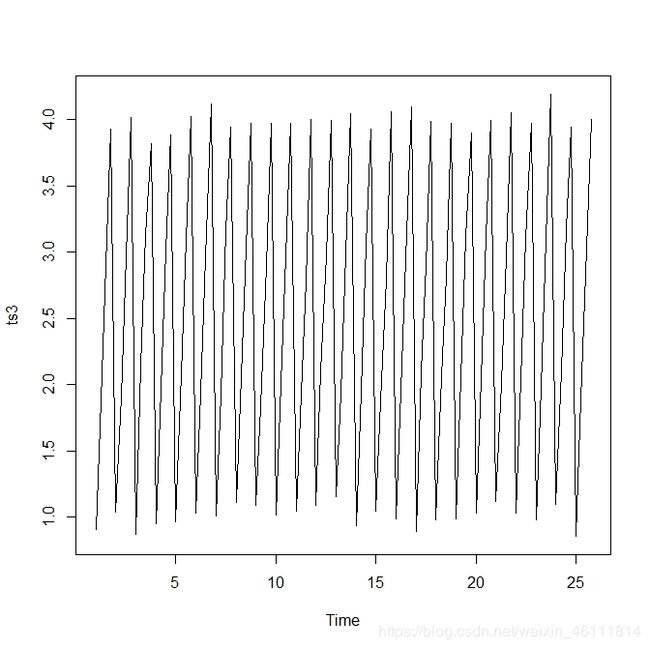
> ts3 <- rep(1:4, time = 25) + rnorm(4*25, 0, 0.1)
> ts3 <- ts(ts3, frequency = 4)
> plot(ts3, type = "l")
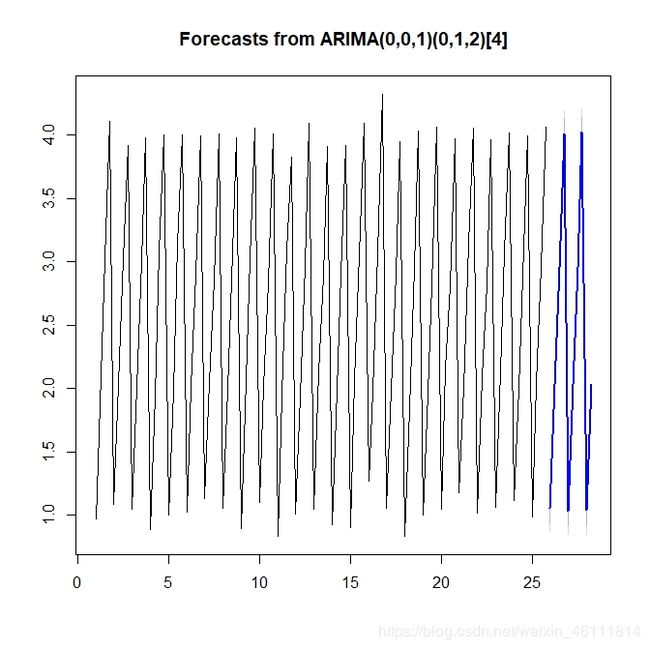
> (fit <- auto.arima(ts3, ic = "aic", max.P = 5, max.Q = 5))
Series: ts3
ARIMA(0,0,0)(4,1,0)[4]
Coefficients:
sar1 sar2 sar3 sar4
-0.6396 -0.5746 -0.4950 -0.3314
s.e. 0.1026 0.1256 0.1219 0.1086
sigma^2 estimated as 0.01478: log likelihood=65.96
AIC=-121.91 AICc=-121.25 BIC=-109.09
> x.fore <- forecast(fit, h = 10)
> plot(x.fore)
3、总结
在使用过程中希望大家仔细识别数据,选择合适的模型。
4、参考文献
https://blog.csdn.net/weixin_46111814/article/details/105348265 ↩︎
https://wenku.baidu.com/view/98d8cb1a6edb6f1aff001ff6.html ↩︎