MATLAB绘制3D隐函数曲面的几种方法

文章来自于MATLAB论坛，见此链接：http://www.ilovematlab.cn/thread-264471-1-1.html，感谢原作者winner245的辛勤总结！

背景介绍
Matlab提供了一系列绘图函数，常见的包括绘制2D曲线的plot函数、绘制2D隐函数曲线的ezplot函数、绘制3D曲面的mesh和surf函数、绘制3D显函数曲面的ezmesh和ezsurf函数。值得注意的是，ez系列的绘图函数里只有ezplot是绘制隐函数曲线的，ezmesh和ezsurf都是画显函数曲面的（不要被ez的名字误解了）。遗憾的是，matlab里并没有提供直接绘制3D隐函数曲面的函数。本帖的目的就是归纳总结几种方便易用的绘制隐函数曲面的办法。

问题描述

如何绘制 3 元方程 f(x, y,z) = 0 确立的隐函数曲面 z = g(x,y) ？其中，方程 f(x, y,z) = 0 无法求解 z 关于 x 、 y 的表达式，即 g(x, y) 的显式表达式无法获取。

准备工作——基础函数介绍

为了解决上述问题，我们需要先 对几个重要的图形函数 isosurface 、 patch 、 isonormals 取得初步的了解，如果您已经对这三个函数很熟悉，可以直接跳过这一步。

l.  isosurface 等值面函数

调用格式： fv = isosurface(X,Y,Z,V,isovalue)

作用：返回某个等值面（由 isovalue 指定）的表面（ faces ）和顶点（ vertices ）数据，存放在结构体 fv 中（ fv 由 vertices 、 faces 两个域构成）。如果是画隐函数 v = f(x,y,z) = 0 的三维图形，那么等值面的数值为 isovalue = 0 。

2.  patch函数

调用格式： patch(X,Y,C) 以平面坐标 (X, Y) 为顶点，构造平面多边形， C 是 RGB 颜色向量

                    patch(X,Y,Z,C) 以空间 3-D 坐标 (X, Y,Z) 为顶点，构造空间 3D 曲面， C 是 RGB 颜色向量

                    patch(fv) 通过包含vertices、faces两个域的结构体fv来构造3D曲面，fv可以直接由等值面函数isosurface得到
例如：patch(isosurface(X,Y,Z,V,0))

3.  isonormals等值面法线函数

调用格式： isonormals(X,Y,Z,V,p)

实现功能：计算等值面 V 的顶点法线，将 patch 曲面 p 的法线设置为计算得到的法线（ p 是 patch 返回得到的句柄）。如果不设置法线的话，得到曲面在过渡地带看起来可能不是很光滑

有了上述三个函数后，我们已经具备间接绘制3D隐函数曲面的能力了。下面以方程
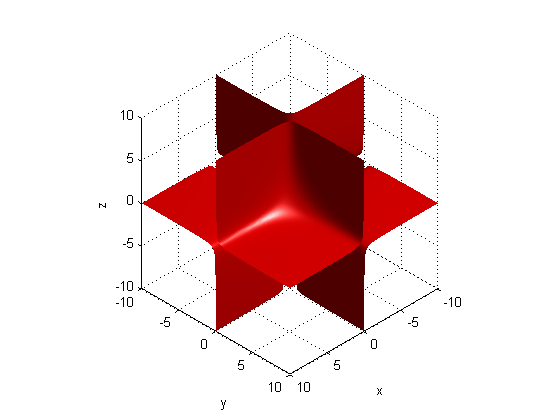
f(x,y, z) = x.*y.*z.*log(1+x.^2+y.^2+z.^2)-10 = 0为例，讲解如何画3D隐函数曲面。

解决办法一：isosurface + patch+ isonormals

实现原理：先定义 3 元显函数 v =f(x, y, z), 则 v = 0 定义的等值面就是 z = g(x,y) 的 3D 曲面。利用 isosurface 函数获取 v= 0 的等值面，将得到的等值面直接输入给 patch 函数，得出 patch 句柄 p ，并画出 patch 曲面的平面视角图形。对 p 用 isonormals 函数设置曲面顶点数据的法线，最后设置颜色、亮度、 3D 视角，得到 3D 曲面。

代码如下：

f = @(x,y,z) x.*y.*z.*log(1+x.^2+y.^2+z.^2)-10;      % 函数表达式
[x,y,z] = meshgrid(-10:.2:10,-10:.2:10,-10:.2:10);       % 画图范围
v = f(x,y,z);
h = patch(isosurface(x,y,z,v,0)); 
isonormals(x,y,z,v,h)              
set(h,'FaceColor','r','EdgeColor','none');
xlabel('x');ylabel('y');zlabel('z'); 
alpha(1)   
grid on; view([1,1,1]); axis equal; camlight; lighting gouraud

代码说明：

• alpha函数用于设置patch曲面的透明度（可以是0~1任意数值），1 表示不透明，0 表示最大透明度。如果想设置透明度为0.7，可以修改alpha(1)为alpha(0.7)。
  

• 使用此代码解决特定问题时，只需将第1行的函数表达式替换为特定问题的函数表达式，将第2行数据（x、y、z）范围换成合适的范围，后续代码无需任何变动。
  

得到图形：

解决办法二：Mupad

Mupad 符号引擎里提供了现成的三维隐函数画图函数： Implicit3d

在 matlab 里开启 Mupad 的方法是：在 commandwindow 里输入 mupad 来启动一个 notebook 。在启动的 notebook 里再输入如下代码：

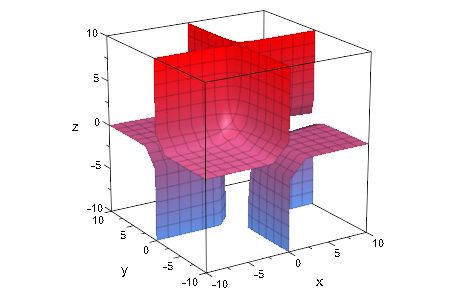
plot(plot::Implicit3d(x*y*z*ln(1+x^2+y^2+z^2)-10,
x = -10..10, y = -10..10, z = -10..10), Scaling = Constrained)

得到如下图形：

解决办法三：第三方工具包ezimplot3

在 matlab central 的 file exchange 上有一个非常优秀的绘制 3 维隐函数的绘图函数，叫 ezimplot3 。感兴趣的可以在如下链接下载：

http://www.mathworks.com/matlabcentral/fileexchange/23623-ezimplot3-implicit-3d-functions-plotter

ezimplot3 一共有三种参数调用方式：

• ezimplot3(f) 画函数f(X,Y,Z)= 0 在-2*pi< X < 2* pi, -2* pi < Y < 2* pi, -2* pi < Z < 2* pi上的图形
• ezimplot3(f, [A,B])画函数f(X,Y,Z)= 0 在A< X < B, A < Y < B, A < Z < B上的图形
• ezimplot3(f, [XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX])画函数f(X,Y,Z)= 0 在XMIN< X < XMAX, YMIN < Y < YMAX, ZMIN < Z < ZMAX上的图形
  
  
  
  

ezimplot3 使用方法：解压 ezimplot3.zip ，将解压得到的 ezimplot3.m 添加到 matlab 当前搜索路径后就可以使用了。 代码为：

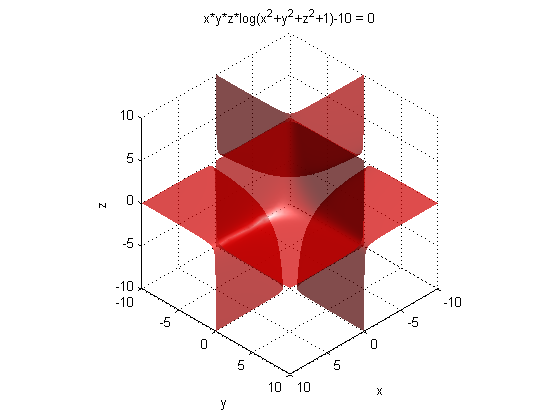
f = @(x,y,z) x*y*z*log(1+x^2+y^2+z^2)-10;
ezimplot3(f,[-10,10]);  % [-10, 10] 表示图形范围x、y、z都在区间[-10, 10]

若干说明：

• ezimplot3和方法一本质上完全相同。即ezimplot3实际上也是基于isosurface+ patch + isonormals的实现
• ezimplot3与方法一的图形视觉效果相同，唯一的区别是，ezimplot3的使用了0.7的透明度：alpha(0.7)
• ezimplot3在方法一基础上增加了一些外包功能，如：允许函数句柄f是非向量化的函数（即函数定义无需.*  ./  .^），这在ezimplot3内部会自动调用vectorize实现函数向量化。另外，ezimplot3可以在调用的时候方便的设定坐标范围。
  

常见问题和解决办法：

• 常见问题：很多人在使用以上方法后，经常出现的问题是代码没有任何错误，程序可以运行，就是出来的图形只有一个空坐标轴，看不到图形。
  

• 问题分析：出现这种问题的原因是图形的显示区域没设对。比如，我们上述三种方法都是在x为-10到10的范围内，如果你设的范围内本身就没有图形，那当然就看不到图形了。
• 解决办法：把图形显示范围重新设置对即可，如果不知道图形的大致范围，就手工多改几次，直到看到图形为止
  

• 方法一，图形范围是在第2句的meshgrid函数决定的，meshgrid里给出的x、y、z范围就是最终画图范围，修改meshgrid语句即可。
• 方法二（Mupad），x =-10..10, y = -10..10, z = -10..10是表示显示范围，修改这里即可。
• 方法三，用ezimplot3(f,[A, B]) ezimplot3(f, [XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX])两种方式控制图形显示范围。
  

后记：slice切片函数

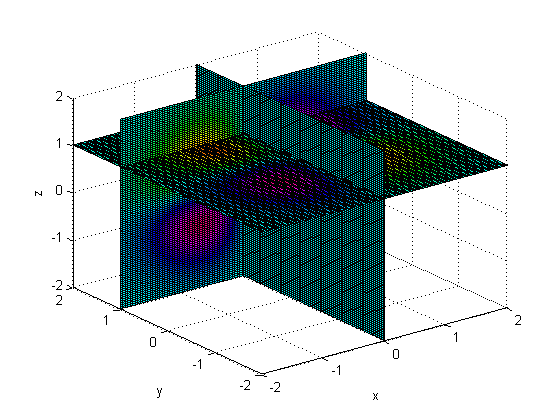
matlab 还提供一种画切片图形的函数 slice ， slice 做出的图是在切片上用颜色表示 v 的值。有时，我们画切片图形也有助于我们理解一个 4 维图形。 以   v= f(x,y,z) = x*y*z*exp(-(x^2+y^2+z^2))   为例，假设我们希望看 v =f(x,y,z) 在 x =0, y = 1, z = 1 这些平面切片的图形，我们可以用以下代码：

[x,y,z] = meshgrid(linspace(-2,2));
v = x.*y.*z.*exp(-(x.^2+y.^2+z.^2));
xslice = 0; yslice = 1; zslice = 1;
slice(x,y,z,v,xslice,yslice,zslice)
xlabel('x'); ylabel('y'); zlabel('z');
colormap hsv 

得到图形为：