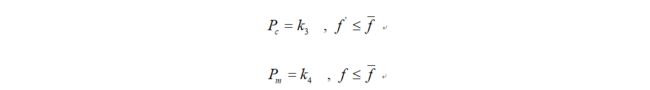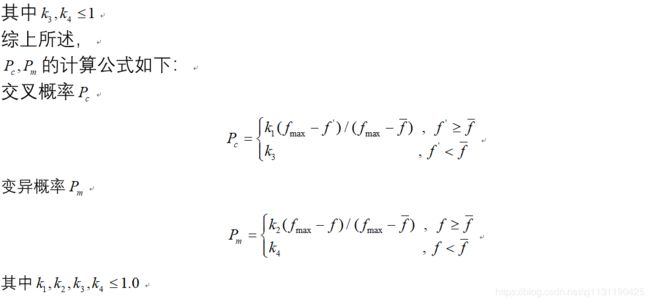基于实数编码的参数自适应遗传算法(matlab代码)
实数编码的遗传算法寻优:
遗传算法的基本操作算子:
(1)选择算子
选择算子的作用主要是避免优良基因的丢失,使得性能高的个体能以更大的概率被选中,有机会作为父代繁殖下一代,从而提 高遗传算法的全局收敛性及计算效率。常见的选择算子包括轮盘赌选择法、随机遍历抽样法、局部选择法及锦标赛选择法等。选择算子采用轮盘赌;
(2)交叉算子
在遗传算法中,交叉算子是区别于其它优化算法的本质特征,用于组合新的个体在解空间中快速有效地进行搜索,同时也降低了对有效模式的破坏程度,起到全局搜索寻优的效果。交叉算子直接影响着遗传算法的最终搜索效果,一定程度上决定了其发展前景。
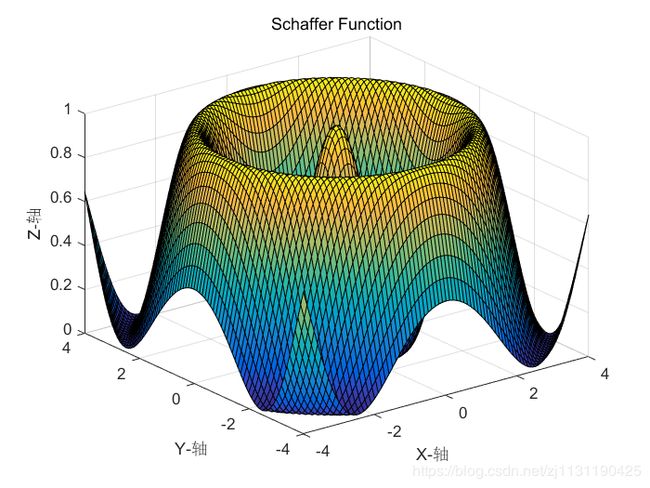
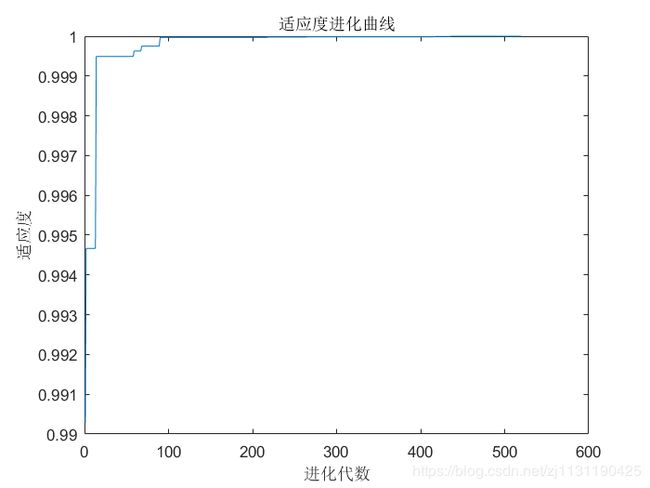
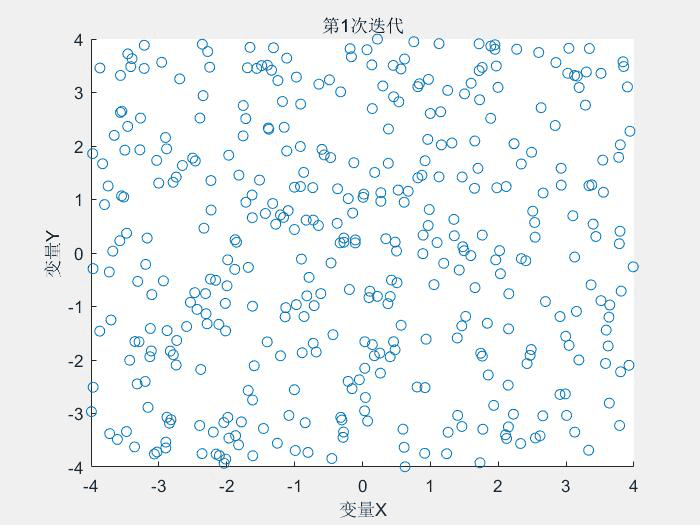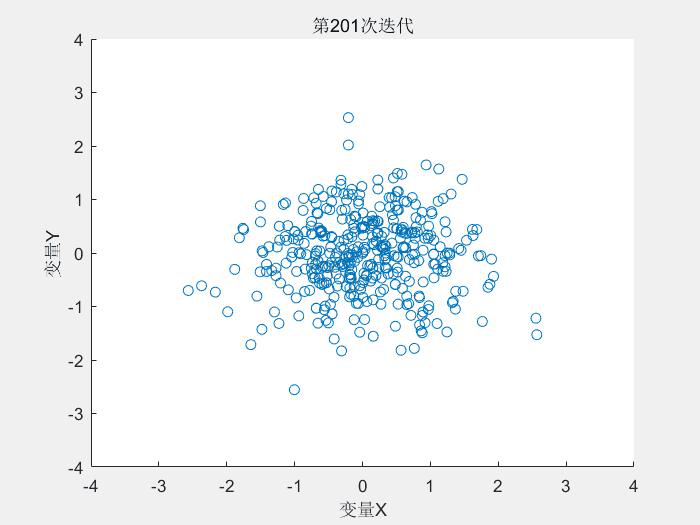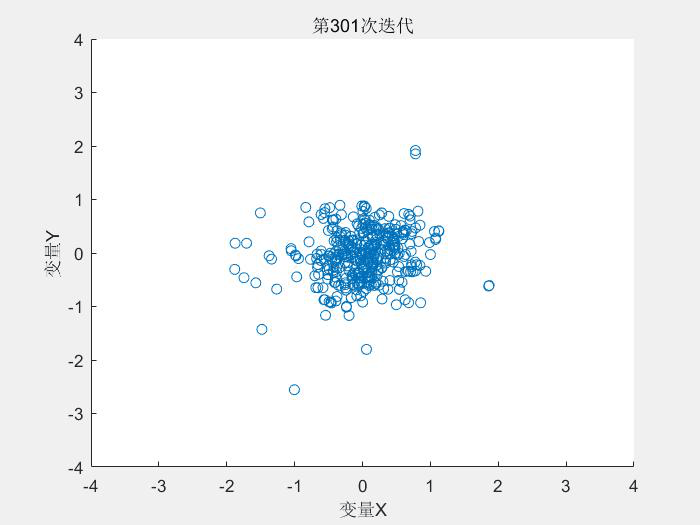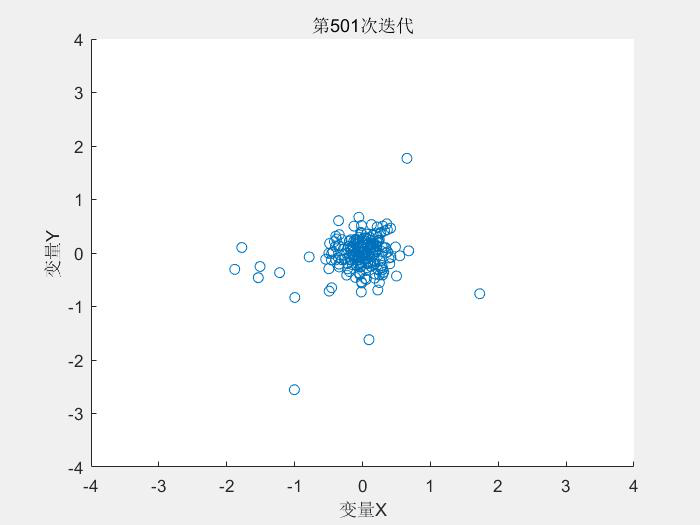
其中alpha为参数,0 (3)变异算子 群体基因的多样性是保证遗传算法寻找到全局最优解的前提条件,然而在进化过程中,遗传选择操作削弱了群体的多样性,上述交叉算子只有满足一定的条件才能保持群体的多样性,而变异操作则是保持群体多样性的有效算子,所以变异操作算子的选取也是必不可少的。变异尺度自适应变化的变异算子在进化初期采用较大的变异尺度来保持群体的多样性,而在后期变异尺度将逐渐缩小以提高局部微调能力。本文在此基础上做些改进,改进后的变异算子具有原有算子的优点,且操作上比原有算子简单方便,有效地加快遗传算法的收敛速度,具体如下: 可以看出s(t) 决定了变异空间的大小,在迭代的初期,变异空间较大,在迭代的后期,变异空间缩小,算法的局部寻优能力变强。 变异算子参考文献: [1] 管小艳. 实数编码下遗传算法的改进及其应用[D].重庆大学,2012. 交叉概率Pc和变异概率Pm是遗传算法的两个重要的参数,这两个参数决定了每个个体进行交叉或者变异操作的概率。 自适应算子参考文献: [2] M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms," in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, April 1994.doi: 10.1109/21.286385 上述部分翻译自文献[2] 按照论文描述,对算法的复现如下: 测试函数: Schaffer函数: 运行结果: 种群的分布变化: -----------------------------------------------------分割线---------------------------------------------------- 2019/4/2 上面的代码有两个地方写错了,现在已经改正: 1. 用于轮盘赌的fitness应该与用于计算自适应参数的fitness分开 2.对轮盘赌选择算子进行修改 修改后的代码: 修改后的算法寻优效果得到很大的提升,非常感谢指出代码中的错误: 运行结果: 参数自适应:
% 测试函数图像
% 测试函数图像
% 改进的自适应遗传算法:
% 参考文献:[7] M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms,"
% in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, April 1994.
% doi: 10.1109/21.286385
clc;
clear all;
mode = 'Schaffer';
% mode = 'self_define';
if strcmp(mode, 'Schaffer')
figure(1)
x = -4:0.1:4;
y = -4:0.1:4;
[X,Y] = meshgrid(x,y);
% Z = 3*cos(X.*Y)+X+Y.^2;
Z = 0.5-((sin(sqrt(X.^2+Y.^2)).^2)-0.5)./(1+0.001.*(X.^2+Y.^2)).^2;
surf(X,Y,Z);
title('Schaffer Function');
xlabel('X-轴');
ylabel('Y-轴');
zlabel('Z-轴');
figure(2);
contour(X, Y, Z, 8);
title('Schaffer函数等高线');
xlabel('X-轴');
ylabel('Y-轴');
end
if strcmp(mode, 'self_define')
figure(1);
x = -4:0.1:4;
y = -4:0.1:4;
[X,Y] = meshgrid(x,y);
% Z = 100.*(Y-X.^2).^2+(1-X).^2;
Z = (cos(X.^2+Y.^2)-0.1)./(1+0.3*(X.^2+Y.^2).^2)+3;
surf(X,Y,Z);
%title('Rosen Brock valley Function');
title('Self define Function');
xlabel('X-轴');
ylabel('Y-轴');
zlabel('Z-轴');
end
clc;
clearvars -except mode;
r = 0.2;
b = 3;
NP=400;
% Pc=0.65; % 将Pc,Pm参数改进为自适应参数
% Pm=0.20;
G=520; % 记得改
D=2; % 变量个数
k1 = 1;
k3 = 1;
k2 = 0.5;
k4 = 0.5;
X_min=-4;
X_max=4;
Y_min=-4;
Y_max=4;
% optimization_trace = []; % 三维数组, 行,列,叶
for count_1=1:NP % 产生初始解
temp1 = X_min+rand()*(X_max-X_min);
temp2 = Y_min+rand()*(Y_max-Y_min);
x(count_1,:) = [temp1,temp2];
end
save_pic_cnt = 1;
A = figure(3);
for gen=1:G
%pause(0.2);
if rem(gen, 100)==1
scatter(x(:,1), x(:, 2));
axis([-4, 4, -4, 4]);
title(['第', num2str(gen), '次迭代']);
xlabel('变量X');
ylabel('变量Y');
base_path = 'C:\Users\18811\Desktop\graph\';
cnt = num2str(save_pic_cnt);
tail_path = '.jpg';
frame = getframe(A);
im=frame2im(frame);
path_img = [base_path, cnt, tail_path];
% imwrite(im, path_img);
% save_x(:, :, save_pic_cnt) = x;
save_pic_cnt = save_pic_cnt + 1;
end
% scatter(0, 0, 'o', 'r');
for count_2=1:NP
fitness(count_2)=func(x(count_2,:), mode);
end
%[fitness_min,index0] = min(fitness);
%fitness_max = max(fitness);
[fitness_max,index0] = max(fitness);
fitness_average = sum(fitness)/(length(fitness)); % 种群的平均值
collect_fit_average(gen) = fitness_average; % 保存适应度的平均值
collect_fitmax_subtract_fit_average(gen) = fitness_max - fitness_average; % 保存f_max-f_average ;
fitness_min = min(fitness);
best_indiv = x(index0,:); % 最优的个体
% optimization_trace(gen,: , global_count) = best_indiv;
% best_solution(gen) = fitness_min;
best_solution(gen) = fitness_max;
% 计算归一化的适应度值
fitness = (fitness - fitness_min)/(fitness_max - fitness_min);
fitness_sum = sum(fitness);
fitness = fitness./fitness_sum;
fitness = cumsum(fitness);
% 选择算子:
ms = sort(rand(NP,1));
fiti = 1;
newi = 1;
while newi<=NP
if ms(newi)% 测试函数图像
% 测试函数图像
% 改进的自适应遗传算法:
% 参考文献:[7] M. Srinivas and L. M. Patnaik, "Adaptive probabilities of crossover and mutation in genetic algorithms,"
% in IEEE Transactions on Systems, Man, and Cybernetics, vol. 24, no. 4, pp. 656-667, April 1994.
% doi: 10.1109/21.286385
clc;
clear all;
mode = 'Schaffer';
% mode = 'self_define';
if strcmp(mode, 'Schaffer')
figure(1)
x = -4:0.1:4;
y = -4:0.1:4;
[X,Y] = meshgrid(x,y);
% Z = 3*cos(X.*Y)+X+Y.^2;
Z = 0.5-((sin(sqrt(X.^2+Y.^2)).^2)-0.5)./(1+0.001.*(X.^2+Y.^2)).^2;
surf(X,Y,Z);
title('Schaffer Function');
xlabel('X-轴');
ylabel('Y-轴');
zlabel('Z-轴');
figure(2);
contour(X, Y, Z, 8);
title('Schaffer函数等高线');
xlabel('X-轴');
ylabel('Y-轴');
end
if strcmp(mode, 'self_define')
figure(1);
x = -4:0.1:4;
y = -4:0.1:4;
[X,Y] = meshgrid(x,y);
% Z = 100.*(Y-X.^2).^2+(1-X).^2;
Z = (cos(X.^2+Y.^2)-0.1)./(1+0.3*(X.^2+Y.^2).^2)+3;
surf(X,Y,Z);
%title('Rosen Brock valley Function');
title('Self define Function');
xlabel('X-轴');
ylabel('Y-轴');
zlabel('Z-轴');
end
clc;
clearvars -except mode;
r = 0.2;
b = 3;
NP=100;
% Pc=0.65; % 将Pc,Pm参数改进为自适应参数
% Pm=0.20;
G=100; % 记得改
D=2; % 变量个数
k1 = 1;
k3 = 1;
k2 = 0.5;
k4 = 0.5;
X_min=-4;
X_max=4;
Y_min=-4;
Y_max=4;
% optimization_trace = []; % 三维数组, 行,列,叶
for count_1=1:NP % 产生初始解
temp1 = X_min+rand()*(X_max-X_min);
temp2 = Y_min+rand()*(Y_max-Y_min);
x(count_1,:) = [temp1,temp2];
end
save_pic_cnt = 1;
A = figure(3);
for gen=1:G
pause(0.2);
if rem(gen, 2)==1
scatter(x(:,1), x(:, 2));
axis([-4, 4, -4, 4]);
title(['第', num2str(gen), '次迭代']);
xlabel('变量X');
ylabel('变量Y');
base_path = 'C:\Users\18811\Desktop\graph\';
cnt = num2str(save_pic_cnt);
tail_path = '.jpg';
frame = getframe(A);
im=frame2im(frame);
path_img = [base_path, cnt, tail_path];
% imwrite(im, path_img);
% save_x(:, :, save_pic_cnt) = x;
save_pic_cnt = save_pic_cnt + 1;
end
% scatter(0, 0, 'o', 'r');
for count_2=1:NP
fitness(count_2)=func(x(count_2,:), mode);
end
fitness_ = fitness;
%[fitness_min,index0] = min(fitness);
%fitness_max = max(fitness);
[fitness_max,index0] = max(fitness);
fitness_average = sum(fitness)/(length(fitness)); % 种群的平均值
collect_fit_average(gen) = fitness_average; % 保存适应度的平均值
collect_fitmax_subtract_fit_average(gen) = fitness_max - fitness_average; % 保存f_max-f_average ;
fitness_min = min(fitness);
best_indiv = x(index0,:); % 最优的个体
% optimization_trace(gen,: , global_count) = best_indiv;
% best_solution(gen) = fitness_min;
best_solution(gen) = fitness_max;
% 计算归一化的适应度值
fitness = (fitness - fitness_min)/(fitness_max - fitness_min);
fitness_sum = sum(fitness);
fitness = fitness./fitness_sum;
fitness = cumsum(fitness);
% 轮盘赌选择
newi = 1;
while newi<=NP
random_num = rand(); % 生成随机数
if random_num