论文阅读笔记《PatchMatch Stereo - Stereo Matching with Slanted Support Windows》

摘要

一般的局部立体方法是在一个具有整型数值视差的支持窗口中进行匹配。其中隐含的一个假设：在支持区域中的像素具有恒定的视差，这个假设在倾斜表面是不成立的，因而倾向于重建前端平行的表面。本论文通过估计每个像素上的一个单独的3D平面，并在此基础上投射出支持区域解决了这种偏差。这种方法的主要挑战是在所有可能无限数量的平面中找到一个像素的最优3D平面。我们证明了PatchMatch算法可以用来解决这个问题，我们把PatchMatch拓展成可以根据一个平面来找到一个近似的最近邻。除了PatchMatch的空间传播方法之外，我们还提出了(1)在立体对的左右视图中传播的图传播，(2)时间传播，在做时间立体时，从视频的前和连续帧中传播平面。自适应支持权值用于聚合匹配代价，以改善视差边界的结果。我们还表明，我们的倾斜支持窗口可以用来计算全球立体方法的代价，它允许明确的遮挡处理，并且可以处理大的非纹理区域。结果表明，我们的方法重构了高度倾斜的表面，并以亚像素精度实现了视差细节。

1 介绍

在局部立体匹配中，支持窗口以参考图像的像素为中心。在第二个图像中，这个支持窗口会被替换，以找到最小颜色不相似性的点，即匹配点。在这个过程中有一个隐含的假设，即在支持窗口内的所有像素都有恒定的视差。实际上，这种假设不太可能成立，原因有两个：(1)支持窗口包含与中心像素位于不同表面的像素。(2)窗口捕捉到倾斜的表面，即,而不是fronto-parallel的。最近有大量的论文解决了问题(1)，而自适应支持权重策略似乎是解决这个问题的最好方法。与此相反，我们处理的问题(2)较少受到关注。

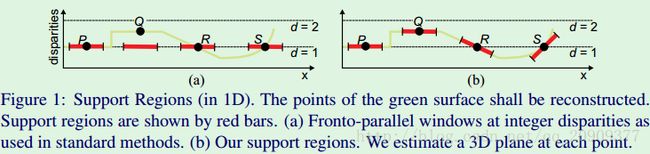
图1a说明了这个问题。标准的局部算法将fronto-parallel窗口应用于离散的视差，以重构图1a的四个点。在我们的例子中，一个最优的支持只能在点P处找到，它的表面部分与在全值视差中的 fronto-parallel平面重合。请注意，这种情况在实际中是非常不可能的。对于所有其他情况下,这种方法不能找到一个最优的支持,因为表面部分位于一个亚像素视差（Q）,或者点位于一个倾斜的（R）或者圆形的（S）平面表面。我们的补救措施是在每个像素计算个体的3D平面，然后通过投影得到支持区域。图1b显示了通过这种方法，得到了非常大改进的支持区域。例如，我们可以对P、Q和R的最优支持建模。我们的平面模型对在S处真实圆形表面形状进行了过度简化。然而，我们将在实验中显示，即使在这种情况下，平面近似也很有效。

目前有几种算法是计算视差图的亚像素精度。通常，亚像素信息是通过在后处理中将cost volumn拟合成一条抛物线而得到的。更复杂的方法(本论文遵循的)是在匹配中直接考虑亚像素精度。在最简单的形式中，这是通过扩展标签空间来完成的，即，除了全值的视差之外，还考虑了一些分数视差值(一半或四分之一像素)。与其在标签空间中添加额外的前端平行平面，还可以添加倾斜的平面。然而，这需要首先提取构成场景的那些平面，考虑到候选平面的数量是无限的，这是一个非常重要的任务。例如，非常流行的基于分割的方法在第一步中使用初始视差图提取了几个平面。在匹配步骤中，检测这些平面以找到每个像素/分割的最适合的一个。这种方法的问题是如果在步骤1中错失了正确的平面，那么匹配的步骤就会失败。这也是局部算法的局限性。

这篇论文提出了一种基于PatchMatch的算法，有效地解决了在每个像素点找到一个“好的”倾斜支持平面的问题。与其他局部算法相比，算法没有构建完整的cost-volume，这在本论文算法中是不可能的，因为标签空间包含了无限个3D平面。相反，算法巧妙地遍历了其中的一部分。这使得一次优化成为可能，平面以及分配给平面的像素能够联合估计，这有效地绕过了错失正确平面的问题。PatchMatch本身就是一个近似稠密的最近邻算法。这篇论文利用随机搜索和传播的PatchMatch思想来寻找平面极线上的最近邻。这使得能够处理倾斜的表面和亚像素精度。

2 算法

2.1 模型

对于两张图像中的每个像素 p ，我们寻找一个平面 fp 。 我们计算左图和右图的视差图，以便通过左右一致性校验来处理遮挡。一旦平面 fp 被找到，我们就可以计算像素 p 的视差：

dp=afppx+bfppy+cfp(1)

其中， afp，bfp，cfp 是平面 fp 的三个参数， px和py 表示像素 p 的 x坐标和y坐标 。平面 fp 是我们期望找到的，使得在所有可能的平面中聚合代价最小的一个平面：

fp=argminf∈ξm(p,f)(2)

其中， ξ 表示所有可能的平面，它的大小是无限的。注意到，这个无限的标签空间使得我们不能想标准的具有离散视差值的局部立体匹配方法那样，只是简单地检查所有可能的标签。与平面 f 对应的匹配像素 p 的聚合代价为：

m(p,f)=∑q∈Wpw(p,q)ρ(q,q−(afpx+bfpy+cf))(3)

其中， Wp 表示一个以像素 p 为中心的方形窗口。但是与现有方法不同， Wp 不再是2D的，而是3D的。权重函数 w(p,q) 用来解决边缘育肥问题，并且实施自适应支持权重的思想。它通过像素之间的颜色来计算它们之间的相似性：

w(p,q)=e−||Ip−Iq||γ(4)

其中， γ 是一个用户定义的参数， ||Ip−Iq|| 计算像素 p和q 在RGB空间中的L1距离。
现在来关注 ρ(q,q′) 部分，首先根据平面 f 计算像素 q 的视差,并且从 q 的x坐标减去这个视差得到在另一张图上的匹配点 q′ ，函数 ρ(q,q′) 现在用来计算像素 q和q′ 之间的不相似性：

p(q,q′)=(1−α)min(||Iq−Iq′||,τcol)+αmin(||∇Iq−∇Iq′||,τgrad)(5)

其中， ||∇Iq−∇Iq′|| 表示像素 p和q 之间的灰度值梯度之差的绝对值。由于像素 q′ 的x坐标在连续区域内，我们通过线性插值来找到它的颜色和梯度值。用户定义的 α 参数用来平衡颜色和梯度项的影响，参数 τcol和τgrad 截断代价，以在遮挡区域获得鲁棒的结果。

2.2 通过PatchMatch方法来计算视差

现在来关注在两张图像中寻找使得方程（3）中的代价最小的3D平面的问题。本论文的方法基于PatchMatch，它的主要思想是：在自然立体对中，相对较大的像素区域可以用近似的平面来模拟。我们通过将每个像素初始化为一个随机的平面来寻找这样一个平面，并且希望通过这样的随机初始化，这个区域中至少有一个像素具有与正确的平面接近的平面。注意，这点很有可能，因为我们有很多猜测，即，这个区域的每个像素代表一个平面。对于算法来说，有一个“好的”猜测已经足够了，因为有一个传播步骤将这个平面传递到该区域的其他像素上。除了对空间相邻像素进行传播外，我们引入了两个新的传播步骤，即:，图传播和时间传播。最后，还有一个平面优化步骤，我们改变平面参数以接近最优平面。
1）随机初始化
给两张图像的每个像素分配一个随机的平面。本论文中，为了给像素 (x0,y0) 计算一个随机的平面，首先选择一个在所允许的连续视差值之间的随机的视差 z0 。这样就给出随机平面中的一个点 P(x0,y0,z0) 。然后计算这个平面的法向量为一个随机的单位向量 n⃗ =(nx,ny,nz) . 把（1）式中的平面表示成 af:=−nxnz,bf:=−nynz,cf:=nxx0+nyy0+nzz0nz
2）迭代
在每一轮迭代中，每个像素都进行以下四个步骤：
(1) spatial propagation空间传播, (2) view propagation图传播,
(3) temporal propagation，(4) plane refinement
我们首先处理左图中的所有像素，然后处理右图中的所有像素。在奇数次迭代中，从左上角的像素开始，逐行遍历像素，直到到达右下角的像素。在偶数次迭代中，我们颠倒顺序，即，从右下角的像素开始，然后在左上方停止。在我们的实验中，我们运行三个迭代。图3是在不同的迭代中得到的结果。

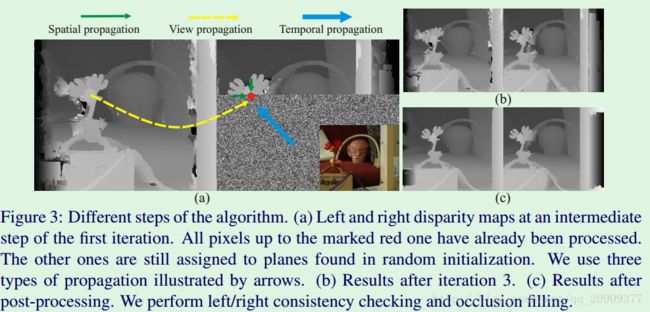
（1）Spatial Propagation空间传播
隐藏在这种传播方式中的想法是，空间上相邻的像素很有可能具有相似的平面。让 p 表示当前像素， fp 是它的平面，我们评估是否将 p 分配给它的空间邻居 q 的平面 fq ,是通过是否可以减小方程(3)的代价为依据，即 m(p,fq)<m(p,fp)) 。如果这个情况满足，则将平面 f(q) 作为像素 p 的新平面。在奇数次循环中，我们考虑左边和上方的邻居，在偶数次循环中，我们考虑右边和下方的邻居。
（2）view propagation图传播
在这里，论文利用了存在于左右视差图之间的强相干性，即，一个像素和它的在一个图像中的匹配点很可能有相似的平面。我们检查根据它们当前的平面以第二个图像中将当前像素p作为匹配点的所有像素。让 p′ 表示这样一个像素， fp′ 表示将它的平面转换为第一张图中对应像素的平面。如果 m(p,fp′)<m(p,fp) ，我们设置 fp：=fp′ .
(3) temporal propagation
这个传播方法仅仅用在立体视频序列中。假设当前视频帧中的像素p和前面帧或后面帧图像中相同坐标上的像素 p′ 可能具有相似的平面。检查条件 m(p,fp′)<m(p,fp) ,如果成立，则设置 fp：=fp′ .（双目匹配这一步不需要）
(4) plane refinement
这一步的目标是精细化平面 fp 的像素 p=(x0,y0) ,以进一步减少方程（3）中的代价。我们把fp转换成点加上法向量表示。我们有两个参数，即， ∇maxz0 定义了3D点的z坐标 z0 的最大允许变化, ∇maxn 限制了法向量 vecn d的分量的允许变化范围。我们现在估计 ∇z0 为一个在区间 [−∇maxz0,∇maxz0] 的随机值,并且计算 z′0:=z0+∇z0 ,这给了我们一个新的3D点 P′=(x0,y0,z′0) 。类似地,我们估计三个随机值的区间 [−∇maxn,∇maxn] ,形成的分量矢量 ∇n→ 。我们现在估计修正的法向量为 n⃗ ′:=u(n⃗ +∇n→) ，其中u()计算单位向量。最后，我们将由 P′和n⃗ ′ 定义的平面转换为由方程(1)的表示形式，得到了修改后的平面 f′p 。如果 m(p,fp′)<m(p,fp) ，我们设置 fp：=fp′ .
这个精细化过程是迭代进行的，我们首先设置 ∇maxz0:=maxdisp/2,masdisp 是所允许的最大视差， ∇maxn:=1 .在每一次精细化后，设置 ∇maxz0:=∇maxz0/2,∇maxn:=∇maxn/2 ,指数减小搜索空间。当 ∇maxz0<0.1 时停止。这个方法允许在第一次迭代时有大的变化，这对于当前平面完全是错误的情况有意义。在后面的迭代中，使得改进的平面非常接近当前的平面，这允许捕获视差细节。

2.3 后处理

通过左/右一致性检查来处理遮挡。对于每个像素p，在另一个图像中计算它的匹配点p’。然后检查条件 dp−dp′≤1 。如果这个条件为假，则像素p是无效的。这种一致性检查通常不能用于遮挡像素，但也适用于误匹配像素。
现在填补无效像素的视差。对于一个无效的像素p，向左和向右搜索它最接近的有效像素。记录两个点的平面 fl和fr 。然后通过式（1）分别计算把p分配到 fl和fr 时的视差，并选择两个中较小的一个作为p的填充视差。选择较小的视差是因为遮挡通常发生在背景中。这种填充模式可以推断出平面，而不是像通常那样复制常数视差。因此，我们也可以在这个阶段正确地对待倾斜的表面。然而，一个明显的问题是这种策略在视差图中产生水平条纹。为了弱化这一问题，我们应用加权中值滤波来处理填充的不均匀性。

2.4 为全局方法建立一个数据项

3 实验结果

未完，待续。。