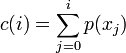图像的直方图均衡

一、直方图均衡化的概念

   图像的直方图：由一幅图像（一般是灰度图像）上的各个灰度值（灰度值在0-255之间）出现的次数（概率）绘图而成。

图1. 原图像

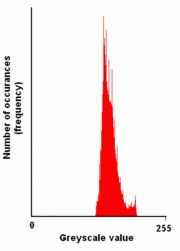
图2. 原图像对应的直方图：横轴表示灰度值，纵轴表示该灰度值在图像上出现的概率（次数）

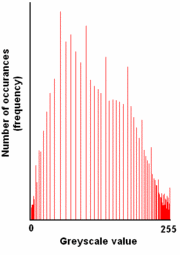
直方图均衡化：是图像处理领域中利用图像直方图对对比度进行调整的方法。理想的图像其直方图分布是比较均衡的，如图3比图1对比度增强，表现在直方图分布上图4比图2要均衡。直方图均衡化实际上就是通过处理，使得一副效果欠佳的图像的直方图能够尽量分布均衡，从而使得处理后的图像对比度增强的技术。

图3. 直方图均衡处理后的图像

图4. 处理后图像对应的直方图

这种方法对于背景和前景都太亮或者太暗的图像非常有用，这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法，亮度可以更好地在直方图上分布。

二、实现算法

    1）直方图计算：计算图像各个灰度值的概率

    看一幅灰度图像，i(i>=0且i<=255)表示灰度值，统计该灰度在图像上出现的次数ni（也就是计算图像上灰度值=i的像素的个数），进而计算灰度为i 的像素的出现概率是：

L 是图像中所有的灰度数，n 是图像中所有的像素数, p 实际上是图像的直方图，归一化到 [0,1]。

   2）累计概率计算

    把 c 作为对应于 p 的累计概率函数, 定义为：

c 是图像的累计归一化直方图，简言之，c（i）的物理意义是灰度值<=i的像素出现的概率。

   3）直方图均衡化处理

    我们创建一个形式为 j= T(i) 的变换，其中，i、j分别是直方图均衡化处理前、后的对应的像素点的灰度值。则转换公式为：

j= T(i) = c(i).

    4）线性化处理：i的取值范围是0-255,c(i)、j的取值范围是0-1，将j的取值范围线性扩展至0-255： j=j*255.

三、程序的大体流程
	读图im；
	获取im的行、列数：row,col;
	for i=0:255	%计算直方图
		计算im上i出现的次数ni；
	    p(i+1)=ni/(row*col);
	end
	%计算累计直方图c
	for s1=1:row	%进行变换处理
		for s2=1:col
			读取原图像对应位置的灰度值i;
			imnew(s1,s2)=c(i+1);进行变换
		end
	end
	%计算imnew的直方图
	%绘图显示im、imnew；
	%绘图显示im、imnew的直方图。

四、matlab程序
[FileName,PathName] = uigetfile('*.jpg','Select the JPG-file');
File=strcat(PathName,FileName);
img=imread(File); %读取文件

if length(size(img))>2 
    img=rgb2gray(img);%如果不是灰度图先转化为灰度图
end
[m,n]=size(img);%m,n分别为行列像素个数
p=zeros(1,256);%统计各灰度数目，共256个灰度级  
for i=0:255
    p(i+1)=length(find(img==i))/(m*n); %计算直方图img中i出现的概率
end
subplot(2,2,1);
imshow(img);title('原图');
subplot(2,2,2);
bar(0:255,p,'b');title('未均衡化的直方图');
%对直方图进行统计
s=zeros(1,256);
for i=1:256
    for j=1:i
        s(i)=p(j)+s(i);
    end
end
a=round(s*255);%对s进行四舍五入
b=img;
for i=0:255
    b(find(img==i))=a(i+1);%将取值范围线性扩展至0-255
end
subplot(2,2,3);
imshow(b);title('均衡化后图像');
for i=0:255
    Gpeq(i+1)=sum(p(find(a==i)));%统计均衡化后的直方图
end
subplot(2,2,4);
bar(0:255,Gpeq,'b');title('均衡化后的直方图');