以太坊椭圆曲线数字签名
本文主要描述椭圆曲线密码学及数字签名相关的理论
椭圆曲线密码学
椭圆曲线密码学(ECC, Elliptic Curve Cryptography)是基于椭圆曲线数学的一种公钥加密方法。
什么是公钥加密方法
在如 DES、AES 这类对称密码系统中,信息的发送方使用一把密钥进行加密,接收方使用相同的密钥进行解密。
而在公钥加密方法中,信息的加密和解密使用的密钥是不同的,称之为公钥和私钥(注:既可以公钥加密私钥解密,也可以私钥加密公钥解密),常用的公钥加密方法有
RSA- 基于大因数分解ECC- 基于椭圆曲线和离散对数
两者都基于数学上一种双向运算,但这种运算一个方向计算容易,反方向计算却十分困难。以RSA背后的因数大数分解理论为例:
笔算完成下面的等式:
373 ∗ 751 = ? 373 * 751 = ? 373∗751=?
如果你用笔在纸上画画 ,会发现这并不是很困难,那么如果是下面的等式呢?
280123 = ? ∗ ? 280123 = ? * ? 280123=?∗?
太困难了 ! 即使是使用计算器,我觉得也没有谁一时半会儿也算不出来。
答案是 373 ∗ 751 = 280123 373 * 751 = 280123 373∗751=280123 ,这就是RSA的理论基础,两个质数(素数)的乘积很容易计算,但要将一个这样的乘积分解回去就困难了。ECC采用的与之类似,不同的是它采用的是离散对数问题(DLP,Discrete Logarithm Problem)制造单向计算的困难(稍后有例子)。
什么是椭圆曲线
我们在中学课本里一定都学过椭圆的定义。如下图所示,
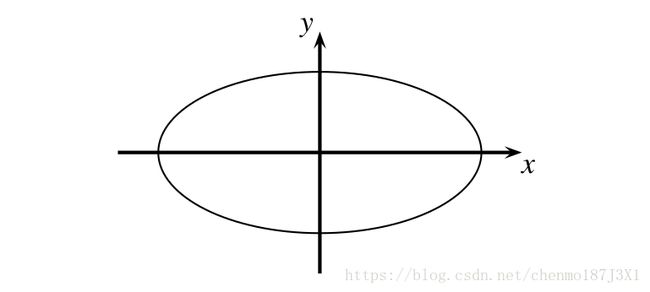
椭圆上的点都满足 a x 2 + b y 2 = c o v e r R ax^2 + by^2= c \quad over \, \mathbb R ax2+by2=coverR
而密码学中的椭圆曲线是满足以下等式的点组成的集合,
y 2 ≡ x 3 + a x + b ( m o d p ) x , y ∈ Z p y^2 \equiv x^3 + ax + b \pmod p \quad x,y \in \Bbb Z_p y2≡x3+ax+b(modp)x,y∈Zp
加上一个想象中的无穷远点 O \mathscr O O ,注意 x , y x,y x,y的取值范围是 Z p = { 1 , 2 , 3... p − 1 } \Bbb Z_p = \{ 1,2,3...p-1\} Zp={1,2,3...p−1}
注:上面的等式需要满足 4 a 3 + 27 b 2 ≠ 0 ( m o d p ) 4a^3 + 27b^2 \neq 0 \pmod p 4a3+27b2̸=0(modp)
举个栗子
椭圆曲线
E : y 2 ≡ x 3 + 2 x + 2 ( m o d 17 ) x , y ∈ Z 17 E :\quad y^2 ≡ x^3+2x+2 \pmod {17} \quad x,y \in \Bbb Z_{17} E:y2≡x3+2x+2(mod17)x,y∈Z17
上的点有 ( 5 , 1 ) (5,1) (5,1) , ( 6 , 3 ) (6,3) (6,3) , ( 10 , 6 ) (10,6) (10,6) , ( 3 , 1 ) (3,1) (3,1) , ( 9 , 16 ) (9,16) (9,16) , ( 16 , 13 ) (16,13) (16,13) , ( 0 , 6 ) (0,6) (0,6) , ( 13 , 7 ) (13,7) (13,7) , ( 7 , 6 ) (7,6) (7,6) , ( 7 , 11 ) (7,11) (7,11) , ( 13 , 10 ) (13,10) (13,10) , ( 0 , 11 ) (0,11) (0,11) , ( 16 , 4 ) (16,4) (16,4) , ( 9 , 1 ) (9,1) (9,1) , ( 3 , 16 ) (3,16) (3,16) , ( 10 , 11 ) (10,11) (10,11) , ( 6 , 14 ) (6,14) (6,14) , ( 5 , 16 ) (5,16) (5,16) 以及 O \mathscr O O。上面的点除了 O \mathscr O O以外,它们是下面曲线上的一些离散的点:
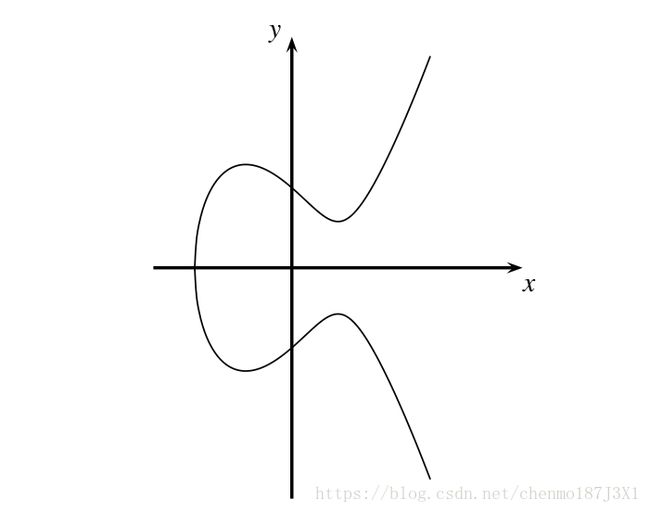
E : y 2 ≡ x 3 + 2 x + 2 ( m o d 17 ) x , y ∈ R E :\quad y^2 ≡ x^3+2x+2 \pmod {17} \quad x,y \in \Bbb R E:y2≡x3+2x+2(mod17)x,y∈R
注意:显然这条曲线是关于 x x x轴对称的,但上面的点的 y y y 坐标都大于0,这是由于 x , y ∈ Z 17 x,y \in \Bbb Z_{17} x,y∈Z17 。举例来说点 ( 5 , 1 ) (5,1) (5,1) 和 ( 5 , 16 ) (5,16) (5,16)实际上就是关于 x x x轴对称的。因为 16 ≡ − 1 ( m o d 17 ) 16\equiv-1 \pmod {17} 16≡−1(mod17),而 ( 5 , − 1 ) (5,-1) (5,−1)也满足 y 2 ≡ x 3 + 2 x + 2 ( m o d 17 ) x , y ∈ R y^2 ≡ x^3+2x+2 \pmod {17} \quad x,y \in \Bbb R y2≡x3+2x+2(mod17)x,y∈R。
.
#####椭圆曲线上的运算规则
椭圆曲线上的点构成的集合中只有一种运算,那就是加法(常数与点的乘法可以看做多个加法),两个点可以进行加法运算得到第三个点,注意,这里的加法不是简单的平面坐标系横纵坐标的相加(这样相加的结果得到的坐标很有可能不在曲线上)。
假设 P = ( x 1 , y 1 ) P=(x_1,y_1) P=(x1,y1)和 Q = ( x 2 , y 2 ) Q=(x_2,y_2) Q=(x2,y2) 都在曲线上,如何得到 R = ( x 3 , y 3 ) R=(x_3,y_3) R=(x3,y3) 使得
P + Q = R ( x 1 , y 1 ) + ( x 2 , y 2 ) = ( x 3 , y 3 ) P+Q=R \\ (x_1,y_1)+(x_2,y_2)=(x_3,y_3) P+Q=R(x1,y1)+(x2,y2)=(x3,y3)
我们从几何学上定义这种加法,有两种情况:
- 两个不同的点相加 P + Q P+Q P+Q 且 P ≠ Q P \neq Q P̸=Q
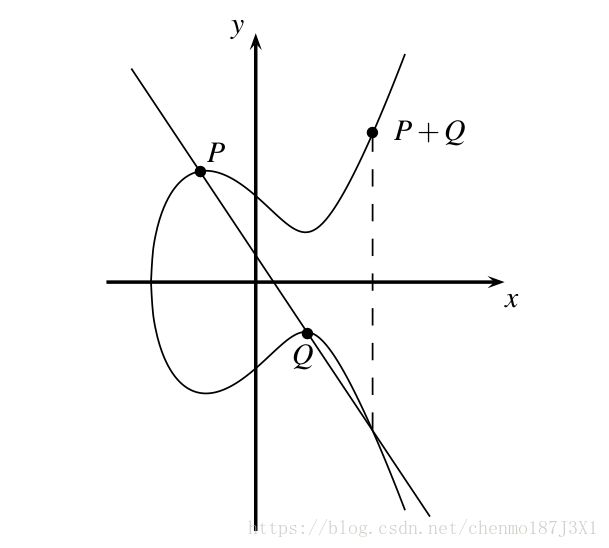
将 P P P 和 Q Q Q 相连的线段延伸,与椭圆曲线有一个交点,该交点关于 x x x轴的对称点就是所求的 P + Q P+Q P+Q
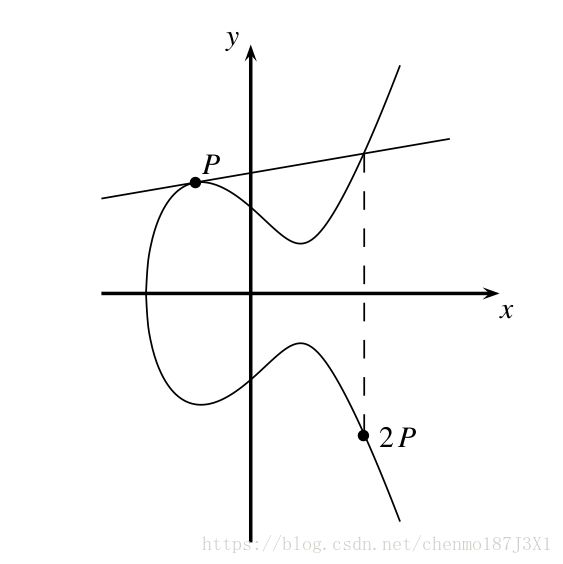
- 一个点自加 P + P P+P P+P
作 P P P在椭圆曲线上的切线,这条切线与椭圆曲线有一个交点,该交点关于 x x x轴的对称点就是所求的 2 P 2P 2P
经过一些数学推导,可以得到计算 R ( x 3 , y 3 ) R(x_3,y_3) R(x3,y3)坐标的公式
x 3 = s 2 − x 1 − x 2 ( m o d p ) y 3 = s ( x 1 − x 3 ) − y 1 ( m o d p ) x_3 = s^2−x_1−x_2 \pmod p \\ y_3 = s(x_1−x_3)−y_1 \pmod p x3=s2−x1−x2(modp)y3=s(x1−x3)−y1(modp)
其中
s = { y 1 − y 2 x 1 − x 2 ( m o d p ) ; P ≠ Q 3 x 1 2 + a 2 y 1 ( m o d p ) ; P = Q s = \left\{ \begin{array}{lr} \dfrac{y_1-y_2}{x_1-x_2} \pmod p ; \quad P \neq Q \\ \dfrac{3x_1^2 +a}{2y_1} \pmod p ; \quad P = Q \end{array} \right. s=⎩⎪⎨⎪⎧x1−x2y1−y2(modp);P̸=Q2y13x12+a(modp);P=Q
还有几个公式,对于 P ( x p , y p ) P(x_p,y_p) P(xp,yp)
P + O = P P + ( − P ) = O − P = ( x p , p − y p ) P+\mathscr O = P \\ P+(-P) = \mathscr O \\ -P = (x_p , p-y_p ) P+O=PP+(−P)=O−P=(xp,p−yp)
生成元
椭圆曲线上所有点加上 O \mathscr O O 包含了很多循环子群(cyclic subgroups) ,其中一个循环子群就是自身,本文仅考虑这种情形。
循环子群中的 生成元(Generator)也被称作素元(primitive element),通过不断自加,它可以**“生成”**群众其他所有元素。那么对本文来说,就是椭圆曲线上的一个点 P P P,通过不断自加,它可以生成椭圆曲线上所有点。
即椭圆曲线上 = { P 、 2 P 、 3 P 、 . . . . n P } \{ P、2P、3P、....nP\} {P、2P、3P、....nP},其中 n n n为循环子群的阶。
再以刚才的例子举例, E : y 2 ≡ x 3 + 2 x + 2 ( m o d 17 ) x , y ∈ Z 17 E :\quad y^2 ≡ x^3+2x+2 \pmod {17} \quad x,y \in \Bbb Z_{17} E:y2≡x3+2x+2(mod17)x,y∈Z17
曲线上的所有点就可以表示为 P P P 的倍数
P = ( 5 , 1 ) 2 P = ( 6 , 3 ) 3 P = ( 10 , 6 ) 4 P = ( 3 , 1 ) 5 P = ( 9 , 16 ) 6 P = ( 16 , 13 ) 7 P = ( 0 , 6 ) P=(5,1) \quad 2P=(6,3)\quad3P=(10,6)\quad4P=(3,1)\quad5P=(9,16)\quad6P=(16,13) \quad 7P=(0,6) P=(5,1)2P=(6,3)3P=(10,6)4P=(3,1)5P=(9,16)6P=(16,13)7P=(0,6)
8 P = ( 13 , 7 ) 9 P = ( 7 , 6 ) 10 P = ( 7 , 11 ) 11 P = ( 13 , 10 ) 12 P = ( 0 , 11 ) 13 P = ( 16 , 4 ) 8P=(13,7)\quad9P=(7,6)\quad10P=(7,11)\quad11P=(13,10)\quad12P=(0,11)\quad13P=(16,4) 8P=(13,7)9P=(7,6)10P=(7,11)11P=(13,10)12P=(0,11)13P=(16,4)
14 P = ( 9 , 1 ) 15 P = ( 3 , 16 ) 16 P = ( 10 , 11 ) 17 P = ( 6 , 14 ) 18 P = ( 5 , 16 ) 19 P = O 14P=(9,1)\quad15P=(3,16)\quad16P=(10,11)\quad17P=(6,14)\quad18P=(5,16)\quad19P=\mathscr O 14P=(9,1)15P=(3,16)16P=(10,11)17P=(6,14)18P=(5,16)19P=O
#####私钥与公钥
之前提到过,椭圆曲线密码系统使用离散对数问题(DLP)构建公钥密码方法,这体现为以下一个事实:
- 计算生成元与一个数 d d d的乘积很容易 d P = ? dP =? dP=? 很容易 (Double-and-Add算法)
- 计算一个点由是由哪个数与生成元相乘得到的很困难 B = ? P B = ?P B=?P
类比与我们熟悉的实数域上,指数运算比对数运算容易得多
而这里 d d d 就是椭圆曲线密码系统中的 私钥, B B B 就是公钥,这也就是为什么可以用私钥推导出公钥,反之不行的原因。
secp256k1
secp256k1是以太坊中使用的椭圆曲线,其参数可以点击Secp256k1 wiki查看,包括椭圆曲线的系数、生成元等。
椭圆曲线数字签名
什么是数字签名
现实生活中的签名作用是签署者对文件进行授权、防止交易中的抵赖发生。
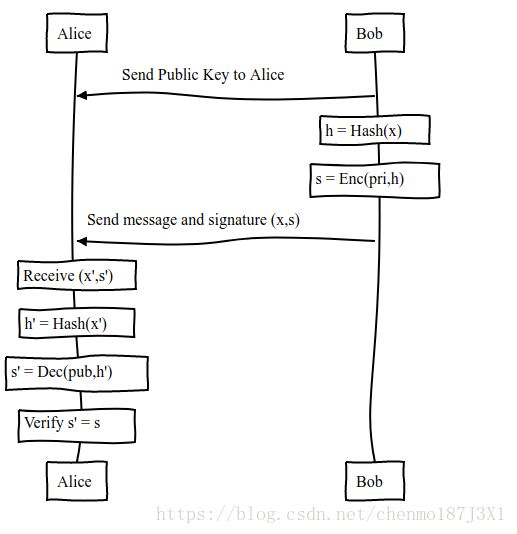
Bob将原文 x x x用特定Hash函数生成摘要 h h h, 用私钥加密 h h h生成签名 s s s,将原文 x x x和摘要 s s s一起传送给Alice。Alice收到后 x ′ x' x′和 s ’ s’ s’,然后用相同的Hash函数将收到消息 x ′ x' x′生成摘要 h ′ h' h′,用Bob的公钥进行解密得到签名 s ’ s’ s’,如果 s = s ’ s = s’ s=s’ 则表示消息是完整的,在传输过程中没有修改。
椭圆曲线数字签名
椭圆曲线数字签名算法(ECDSA)就是利用椭圆曲线加密方法进行数字签名的方法。
设我们使用的曲线 y 2 ≡ x 3 + a x + b ( m o d p ) x , y ∈ Z p y^2 \equiv x^3 + ax + b \pmod p \quad x,y \in \Bbb Z_p y2≡x3+ax+b(modp)x,y∈Zp ,
其生成元 A A A的阶数为 q q q,私钥为 d d d,则公钥 B = d A B = dA B=dA
发送方签名
- 选择一个随机的key k E k_E kE,满足 0 < k E < q 0<k_E<q 0<kE<q
- 计算 R = k E A R = k_EA R=kEA
- 令 r ≡ x R ( m o d p ) r \equiv x_R \pmod p r≡xR(modp) ,即 r r r 为 R R R 的 x x x 坐标对 p p p 求模
- 计算 s ≡ ( h ( x ) + d ⋅ r ) k E − 1 ( m o d q ) s \equiv (h(x) + d \cdot r)k_E^{-1} \pmod q s≡(h(x)+d⋅r)kE−1(modq)
则生成的 ( r , s ) (r,s) (r,s) 就是数字签名。之后发送方将 ( s , ( r , s ) ) (s,(r,s)) (s,(r,s)) 发送给接收方
接收方验证
- 计算 u 1 ≡ s − 1 ⋅ h ( x ) ( m o d q ) u_1 \equiv s^{-1} \cdot h(x) \pmod q u1≡s−1⋅h(x)(modq)
注1 - 计算 u 2 ≡ s − 1 ⋅ r ( m o d q ) u_2 \equiv s^{-1} \cdot r \pmod q u2≡s−1⋅r(modq)
- 计算 P = u 1 A + u 2 B P = u_1A + u_2B P=u1A+u2B
- 进行验证 x P = { ≡ r ( m o d q ) → 签 名 有 效 ̸ ≡ r ( m o d q ) → 签 名 无 效 x_P = \left\{ \begin{array}{lr} \equiv r \pmod q \rightarrow 签名有效 \\ \not\equiv r \pmod q \rightarrow 签名无效 \end{array} \right. xP={≡r(modq)→签名有效̸≡r(modq)→签名无效
注1:这里的 − 1 ^{-1} −1表示在模运算中求逆,在 Z p \Bbb Z_p Zp中,一个数 a a a 与它的逆 a − 1 a^{-1} a−1 满足 a ⋅ a − 1 ≡ 1 ( m o d p ) a \cdot a^{-1} \equiv 1 \pmod p a⋅a−1≡1(modp)
理论(不感兴趣可看例子)
由 s ≡ ( h ( x ) + d ⋅ r ) k E − 1 ( m o d q ) s \equiv (h(x) + d \cdot r)k_E^{-1} \pmod q s≡(h(x)+d⋅r)kE−1(modq)
两边同时乘以 k E ⋅ s − 1 k_E \cdot s^{-1} kE⋅s−1 可得 k E ≡ s − 1 ( h ( x ) + d ⋅ r ) ( m o d q ) k_E \equiv s^{-1}(h(x) + d \cdot r) \pmod q kE≡s−1(h(x)+d⋅r)(modq)
然后 k E ≡ s − 1 h ( x ) + d ⋅ s − 1 ⋅ r ( m o d q ) k_E \equiv s^{-1}h(x) + d \cdot s^{-1} \cdot r \pmod q kE≡s−1h(x)+d⋅s−1⋅r(modq)
即 k E ≡ u 1 + u 2 d ( m o d q ) k_E \equiv u_1 + u_2d \pmod q kE≡u1+u2d(modq)
同时计算对 生成元 A A A的数乘,由于 B = d A B = dA B=dA k E A = u 1 A + u 2 B k_EA = u_1A + u_2B kEA=u1A+u2B
即 R = u 1 A + u 2 B R = u_1A + u_2B R=u1A+u2B
所以只要接收方计算的 P P P 的 x x x 坐标等于 R R R 的 x x x 坐标 r r r ,则可说明验证通过 (之所以看 x x x 坐标是因为椭圆曲线中,只凭一个点的 x x x 坐标并不能唯一确定它的 y y y 坐标)
例子
以曲线 E : y 2 ≡ x 3 + 2 x + 2 ( m o d 17 ) E: y^2 \equiv x^3 + 2x + 2 \pmod {17} E:y2≡x3+2x+2(mod17) 为例,生成元 A = ( 5 , 1 ) A = (5,1) A=(5,1)

数字签名恢复公钥
在上面的例子中,Bob 首先需要向 Alice 告知它的公钥,但实际上,我们凭签名 ( r , s ) (r,s) (r,s) 就恢复出公钥, 在以太坊中使用 /crypto/secp256k1/secp256.go 中的 RecoverPubkey()函数完成这一功能。
理论
接收方收到的信息包括原文和签名: ( x , ( r , s ) ) (x, (r, s)) (x,(r,s)) ,从 x x x 可以计算出 h ( x ) h(x) h(x) ,除此之外接收方就只知道椭圆曲线的参数了,如 ( a , b , p , q , A ) (a, b, p, q, A) (a,b,p,q,A) ,要注意它不知道 ( d , k E ) (d, k_E) (d,kE),而我们的目标是在不知道 d d d 的情况下求出 B B B。
由之前推导出的下式开始 k E ≡ s − 1 h ( x ) + d ⋅ s − 1 ⋅ r ( m o d q ) k_E \equiv s^{-1}h(x) + d \cdot s^{-1} \cdot r \pmod q kE≡s−1h(x)+d⋅s−1⋅r(modq)
两边同时 A A A 数乘 得到 R = s − 1 h ( x ) A + s − 1 B R = s^{-1}h(x)A + s^{-1}B R=s−1h(x)A+s−1B
表示出 B B B B = r − 1 ( s R − h ( x ) A ) B= r^{-1}(sR - h(x)A) B=r−1(sR−h(x)A)
观察上式可知,只要知道了 R R R 点坐标,我们就可以算出 B B B ,但我们没有 R R R 点坐标, 不过我们有它的 x x x 轴坐标 r r r 注2 ,我们可以将其代入曲线方程,反解出 R R R 点 y y y 坐标,但由于椭圆曲线是关于 x x x 轴对称的,所以我们可以解出两个符合条件的 B B B
注2:我们这里忽略 r < p − q r < p - q r<p−q 的情景,这种情况很罕见(在Secp256k1曲线中,大约是 2 − 128 2^{-128} 2−128),在这种情况下 ,有两个 x R x_R xR都能满足条件。
例子
注意以下椭圆曲线上的点的计算过程中
- 数乘运算使用Double-and-Add算法
- 加法运算代入 P + Q P +Q P+Q 的坐标公式计算
以刚才的椭圆曲线数字签名为例,Alice 收到Bob带有签名的消息时,她自己有以下信息 (没有了Bob的公钥 B B B )
- 椭圆曲线参数 E : y 2 ≡ x 3 + 2 x + 2 ( m o d 17 ) x , y ∈ Z 17 E :\quad y^2 ≡ x^3+2x+2 \pmod {17} \quad x,y \in \Bbb Z_{17} E:y2≡x3+2x+2(mod17)x,y∈Z17 生成元 A = ( 5 , 1 ) A = (5, 1) A=(5,1) 阶数 q = 19 q = 19 q=19。
- ( r , s ) = ( 7 , 17 ) h ( x ) = 26 (r, s) = (7, 17) \quad h(x) = 26 (r,s)=(7,17)h(x)=26
计算 h ( x ) A = 26 ∗ ( 5 , 1 ) = ( 0 , 6 ) h(x)A = 26*(5,1) = (0,6) h(x)A=26∗(5,1)=(0,6)
由 $ r = 7 $ , 7 ∗ 11 ≡ 1 ( m o d 19 ) 7 *11 \equiv 1 \pmod {19} 7∗11≡1(mod19) 得到 r − 1 ≡ 11 ( m o d 19 ) r^{-1} \equiv 11 \pmod {19} r−1≡11(mod19)
再将 $ r = 7 $ ,代入曲线方程,得到 R R R 点的坐标为 ( 7 , 6 ) (7,6) (7,6) 或 ( 7 , 11 ) (7,11) (7,11)
-
当 R = ( 7 , 6 ) R=(7,6) R=(7,6) 时
s R = 17 ∗ ( 7 , 6 ) = ( 5 , 1 ) sR = 17*(7,6) = (5, 1) sR=17∗(7,6)=(5,1)
所以 B = r − 1 ( s R − h ( x ) A ) = 11 ( ( 5 , 1 ) − ( 0 , 6 ) ) = 11 ( ( 5 , 1 ) + ( 0 , 11 ) ) = 11 ( 16 , 4 ) = ( 7 , 11 ) B= r^{-1}(sR - h(x)A) = 11((5,1) - (0,6)) = 11((5,1) + (0,11)) = 11(16, 4) = (7,11) B=r−1(sR−h(x)A)=11((5,1)−(0,6))=11((5,1)+(0,11))=11(16,4)=(7,11) -
当 R = ( 7 , 11 ) R=(7,11) R=(7,11) 时
s R = 17 ∗ ( 7 , 11 ) = ( 5 , 16 ) sR = 17*(7,11) = (5, 16) sR=17∗(7,11)=(5,16)
所以 B = r − 1 ( s R − h ( x ) A ) = 11 ( ( 5 , 16 ) − ( 0 , 6 ) ) = 11 ( ( 5 , 16 ) + ( 0 , 11 ) ) = 11 ( 13 , 10 ) = ( 0 , 6 ) B= r^{-1}(sR - h(x)A) = 11((5,16) - (0,6)) = 11((5,16) + (0,11)) = 11(13, 10) = (0,6) B=r−1(sR−h(x)A)=11((5,16)−(0,6))=11((5,16)+(0,11))=11(13,10)=(0,6)
最终我们可以得到 两个符合条件的公钥 B = ( 7 , 11 ) B = (7,11) B=(7,11) 和 B = ( 0 , 6 ) B = (0,6) B=(0,6) , 而无论是哪一个都可以得出相同的签名
参考资料
[1] Understanding Cryptography, Christof Paar / Jan Pelzl
[2] https://en.bitcoin.it/wiki/Secp256k1