高等数学:第八章 多元函数的微分法及其应用(2)偏导数
§8.2 偏导数
一、偏导数定义、计算法及几何意义
1、定义
由于多元函数的自变量不止一个,因变量与自变量的关系要比一元函数复杂得多。本节,我们以二元函数![]() 为例,考虑二元函数关于其中一个自变量的变化率的问题。
为例,考虑二元函数关于其中一个自变量的变化率的问题。
若只有自变量![]() 变化,而自变量
变化,而自变量![]() 固定(即看作常量),这时,
固定(即看作常量),这时,![]() 就成了一元函数,这个函数对于
就成了一元函数,这个函数对于![]() 的导数,就称之为二元函数
的导数,就称之为二元函数![]() 对于
对于![]() 的偏导数。
的偏导数。
【定义】设函数![]() 在点
在点![]() 的某一邻域内有定义,当
的某一邻域内有定义,当![]() 固定在
固定在![]() ,而
,而![]() 在
在![]() 处有增量
处有增量![]() 时,相应地函数有增量
时,相应地函数有增量
![]()
如果极限
存在,则称此极限为函数![]() 在点
在点![]() 处对
处对![]() 的偏导数,并记作
的偏导数,并记作
类似地,函数![]() 在点
在点![]() 处对
处对![]() 的偏导数定义为
的偏导数定义为
如果函数![]() 在区域
在区域![]() 内每一点
内每一点![]() 处对
处对![]() 的偏导数都存在,那未这个偏导数就是
的偏导数都存在,那未这个偏导数就是![]() 的函数,称它为函数
的函数,称它为函数![]() 对自变量
对自变量![]() 的偏导函数,记作
的偏导函数,记作 ![]() 。
。
类似地,可以定义函数![]() 对自变量
对自变量![]() 的偏导函数,并记作
的偏导函数,并记作
由偏导函数概念可知,![]() 在点
在点![]() 处对
处对![]() 的偏导数
的偏导数![]() ,其实就是偏导函数
,其实就是偏导函数![]() 在点
在点![]() 处的函数值;
处的函数值;![]() 就是偏导函数
就是偏导函数![]() 在点
在点![]() 处的函数值。
处的函数值。
在不产生混淆的情况下,我们以后把偏导函数也简称为偏导数。
2、计算法
求![]() 的偏导数,并不需要新的方法,因为这里只有一个自变量在变化,另一自变量被看成是固定的,所以仍然是一元函数的导数。
的偏导数,并不需要新的方法,因为这里只有一个自变量在变化,另一自变量被看成是固定的,所以仍然是一元函数的导数。
求![]() 时,把
时,把![]() 看作常量,而对
看作常量,而对![]() 求导数;
求导数;
求![]() 时,把
时,把![]() 看作常量,而对
看作常量,而对![]() 求导数。
求导数。
显然,偏导数的概念可推广到三元以上的函数情形。
例如,三元函数![]() 在点
在点![]() 处对
处对![]() 的偏导数是如下极限
的偏导数是如下极限
【例1】求![]() 在点
在点![]() 处的偏导数。
处的偏导数。
【解法二】 ![]() ,
, ![]()
则 ![]()
![]()
注:求多元函数在某点处的偏导数时,解法二有时会方便一些。
【例2】设 ![]() (
( ![]() ,
, ![]() ,
,![]() 为任意实数 )
为任意实数 )
【例3】已知理想气体的状态方程为![]() (
( ![]() 为常量 ),
为常量 ),
注:偏导数的记号应看作一个整体性的符号(不能看成商的形式),这与一元函数导数![]() 可看作函数微分
可看作函数微分![]() 与自变量微分
与自变量微分![]() 之商是有区别的。
之商是有区别的。
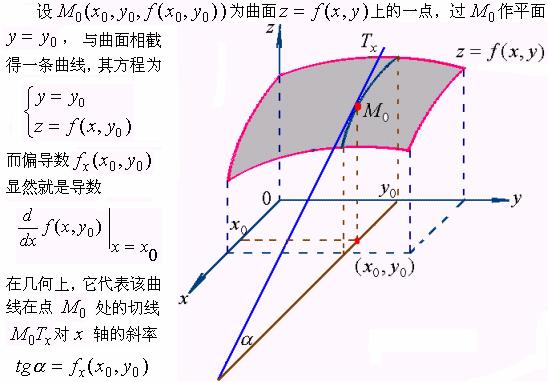
3、几何意义
同样,偏导数![]() 表示曲面
表示曲面![]() 被平面
被平面![]() 所截得的曲线
所截得的曲线 在点
在点![]() 处的切线对
处的切线对![]() 轴的斜率。
轴的斜率。
4、二元函数的偏导数与连续性之间的关系
一元函数在某点可导,则函数在该点一定连续;若函数在某点不连续,则函数在该点一定不可导。对于二元函数来说,情况就不同了。
二元函数![]() 在点
在点![]() 处的偏导数
处的偏导数![]() 、
、![]() ,仅仅是函数沿两个特殊方向( 平行于
,仅仅是函数沿两个特殊方向( 平行于![]() 轴、
轴、![]() 轴 )的变化率;而函数在
轴 )的变化率;而函数在![]() 点连续,则要求点
点连续,则要求点![]() 沿任何方式趋近于点
沿任何方式趋近于点![]() 时,函数值
时,函数值![]() 趋近于
趋近于![]() ,它反映的是函数
,它反映的是函数![]() 在
在![]() 点处的一种“全面”的性态。
点处的一种“全面”的性态。
因此,二元函数在某点偏导数与函数在该点的连续性之间没有联系。
【反例一】讨论函数
在点![]() 处的偏导数与连续性。
处的偏导数与连续性。
函数沿过原点的直线![]() 趋近于原点时,其极限值与参数
趋近于原点时,其极限值与参数![]() 有关,故二重极限不存在,函数在原点自然是不连续的。
有关,故二重极限不存在,函数在原点自然是不连续的。
函数关于自变量![]() 是对称的,故
是对称的,故
![]()
此例表明,二元函数在一点不连续,但其偏导数却存在。
【反例二】讨论函数
![]()
在点![]() 处的偏导数与连续性。
处的偏导数与连续性。
据对称性,![]() 也不存在。
也不存在。
此例表明,二元函数在一点连续,但在该点的偏导数不存在。
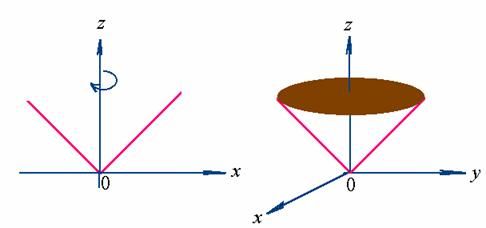
在几何上,曲面![]() 可看成是折线
可看成是折线![]() 绕
绕![]() 轴旋转而成的锥面,点
轴旋转而成的锥面,点![]() 是曲面的尖点。
是曲面的尖点。
二、高阶偏导数
设函数![]() 在区域
在区域![]() 内具有偏导数
内具有偏导数
于是,在![]() 内
内![]() 、
、![]() 均是
均是![]() 的函数,若这两个函数的偏导数也存在,则称它们是函数的二阶偏导数。
的函数,若这两个函数的偏导数也存在,则称它们是函数的二阶偏导数。
按照对变量求导次序有下列四种二阶偏导数
其中:称![]() 、
、![]() 为二阶混合偏导数,类似地,可得到三阶、四阶和更高阶的导数。二阶及二阶以上的偏导数统称为高阶偏导数。
为二阶混合偏导数,类似地,可得到三阶、四阶和更高阶的导数。二阶及二阶以上的偏导数统称为高阶偏导数。
对于二阶偏导数的符号,有必要引入如下简洁记法:
在不特别需要写出函数自变量时,二阶偏导数的符号还可简单的记成
【例4】求函数![]() 的二阶偏导数。
的二阶偏导数。
此例中的两个二阶混合偏导数相等,即 ,这并不是某种偶然的巧合,其实,我们有如下定理。
,这并不是某种偶然的巧合,其实,我们有如下定理。
【定理】如果函数![]() 的两个二阶混合偏导数
的两个二阶混合偏导数![]() 及
及![]() 在区域内连续,那未在该区域内这两个二阶混合偏导数必相等。
在区域内连续,那未在该区域内这两个二阶混合偏导数必相等。
这一结论表明,有二阶混合偏导数连续的条件下,它与求导次序无关。
对于二元以上的函数,我们可类似地定义高阶偏导数,而且高阶混合偏导数在偏导数连续的条件下也与求导的次序无关。
必须指出,定理中所要求的条件连续是必要的,改变这一条件,定理的结论不真。
【例5】证明函数
在原点处的两个二阶混合偏导数存在,但不相等。
证明:当![]() 时,
时,
当![]() 时,
时,
即
注意到,将函数中的变量![]() 与
与![]() 对调,函数却改变符号,于是有
对调,函数却改变符号,于是有
这里 ![]() , 显然,两个一阶偏导函数在原点是不连续的。
, 显然,两个一阶偏导函数在原点是不连续的。
由于函数关于自变量是对称的,因此