均分纸牌问题总结【线形、环形、二维】

线形均分纸牌问题

题意

有N堆纸牌，编号分别为 1,2,…,N。每堆上有若干张，但纸牌总数必为 N 的倍数。
可以在任一堆上取若干张纸牌，然后移动。
移牌规则为：在编号为 1 的堆上取的纸牌，只能移到编号为 2 的堆上；在编号为 N 的堆上取的纸牌，只能移到编号为 N−1 的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。
现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

思路

第一堆牌只能给第二堆牌（给正负张都可以）
那么第一堆牌的值是不是平均值就决定：是否要对第一堆牌进行操作（第二堆给第一堆牌）
第一堆考虑完之后，第二堆成为“没有考虑的序列的”第一堆 ----- 进行判断：前i堆之和与（avg*i）比较

代码

#include
using namespace std;
const int N=1e6+10;
int a[N],sum[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    int res = 0;
    for(int i=1;i<=n;i++) sum[i] = sum[i-1] +a[i];
    int avg = sum[n] / n;
    for(int i=1;i<=n;i++)
    {
        if(sum[i] != avg *(i))
            res++;
    }
    cout<<res<<endl;
    return 0;
}

环形均分纸牌问题

题意

第一个问题的基础上
第一个人可以将自己的牌给最后一个人，也可以从最后一个人哪里拿牌； 最后一个人同理； 询问这个时候需要的最小代价
最小代价是：移动一张牌代价为1

题目链接

思路

画滴属实难看
a1，a2，a3 — an为原序列，avg为序列的平均值（也是均分之后的值

！！ 化解到3之后，把常数符号之后为

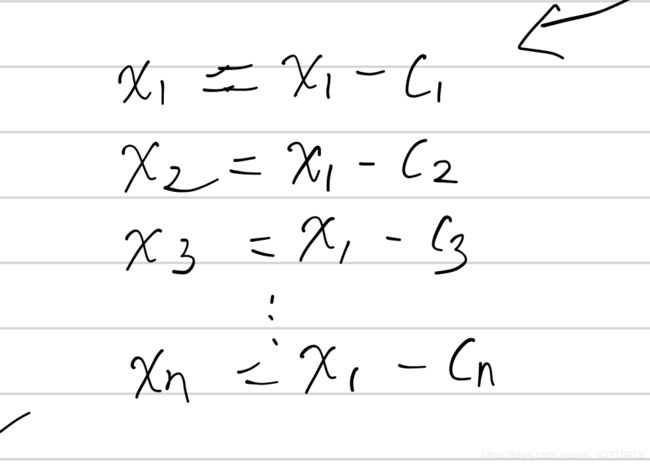
这里是经典的中位数性质：把c1，c2，c3 — - cn，看为坐标轴上点，x1为不确定的点
求|x1|+|x2|+ - - -+|xn| = |x1-c1| + |x2-c2| + |xn-cn|
等价与分别与c1，c2，c3—cn的中位数，相减求绝对值再相加

代码

#include
using namespace std;
const int N=1e6+100;
typedef long long ll;
ll a[N],sum[N];
ll c[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<=n;i++) sum[i]=sum[i-1] + a[i];
    
    ll avg = sum[n] / n;
    c[1]=0;
    for(int i=2;i<=n;i++)
    {
        c[i] = sum[i-1] - (i-1)*avg ;
    }
    sort(c+1,c+1+n);
    ll res=0;
    for(int i=1;i<=n;i++)
        res += abs(c[i] - c[(n+1)/2]);
    cout<<res<<endl;
    return 0;
}

二维均分纸牌问题

题目链接

思路

左右交换：行总和是不变的、列总和变化
上下交换：列总和上不变的、行总和变化
先左右交换：求一次环形均分纸牌，再求上下交换的环形均分纸牌

代码

#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010;

int row[N], col[N], s[N], c[N];

LL work(int n, int a[])
{
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];

    if (s[n] % n) return -1;

    int avg = s[n] / n;

    c[1] = 0;
    for (int i = 2; i <= n; i ++ ) c[i] = s[i - 1] - (i - 1) * avg;

    sort(c + 1, c + n + 1);
    LL res = 0;
    for (int i = 1; i <= n; i ++ ) res += abs(c[i] - c[(n + 1) / 2]);

    return res;
}

int main()
{
    int n, m, cnt;
    scanf("%d%d%d", &n, &m, &cnt);

    while (cnt -- )
    {
        int x, y;
        scanf("%d%d", &x, &y);
        row[x] ++, col[y] ++ ;
    }

    LL r = work(n, row);
    LL c = work(m, col);

    if (r != -1 && c != -1) printf("both %lld\n", r + c);
    else if (r != -1) printf("row %lld\n", r);
    else if (c != -1) printf("column %lld\n", c);
    else printf("impossible\n");

    return 0;
}