5.22 力扣 滑动窗口 前缀和应用 单调栈（768）

1248. 统计「优美子数组」


法一：滑动窗口
例如 nums=[1,2,1,1,2,2,1,2,1]，k=2
stack=[0,1,3,4,7,9],0和9是增加的边界
当i=1,符合条件的最小数组是第一个1和第三个1之间，即 nums[0]-nums[2],则左边界的可能的点是stack[1]-stack[0],右边界可能的点是stack[i+k]-stack[i+k-1]即(stack[3]-stack[2])

class Solution:
    def numberOfSubarrays(self, nums: List[int], k: int) -> int:
        stack=[0] #给数组增加一个左边界（上一个奇数位置）
        for i in range(len(nums)):
            if nums[i]%2:
                stack.append(i+1)#将数组中奇数的索引压入，与原始0做区分，都加1
        stack.append(len(nums)+1) # len(nums)+1代表最后一个奇数位之后的奇数位置(fake point)
        count=0
        for i in range(1,len(stack)-k):
             # 当前奇数位置 i 到前一个奇数位置之间的点都可以作为符合条件的子数组的左边界 ， i 后的第 k-1 个奇数的位置到 i 后的第 k 个奇数节点范围内的点都可以作为符合条件的子数组的右边界
             #可以不选择偶数，所以左边界有(stack[i]-stack[i-1])种可能，包括位置i的奇数
             #右边界有stack[i+k]-stack[i+k-1]种可能，包括位置i+k-1处的奇数
            count+=(stack[i]-stack[i-1])*(stack[i+k]-stack[i+k-1])
        return count

922. 按奇偶排序数组 II

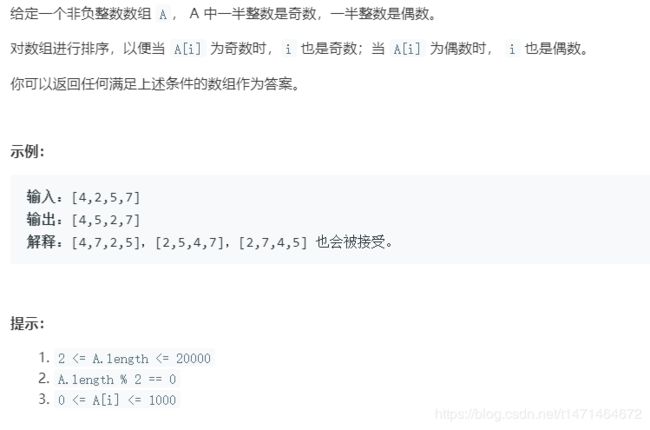
当偶数位是奇数时，一定存在有奇数位是偶数
使用两个指针 i,j分别遍历奇数位和偶数位，保证i,j之前的数据都放在了合适的位置

class Solution:
    def sortArrayByParityII(self, A: List[int]) -> List[int]:
        j=1
        for i in range(0,len(A),2):
        #当遇到偶数位放的是奇数时，查找第一个奇数位存放的偶数的下标，交换两个值，保证i,j之前的数据都放在了合适的位置
            if A[i]%2:
                while A[j]%2 and j<=len(A):
                    j+=2
                A[i],A[j]=A[j],A[i]
        return A

面试题59 - II. 队列的最大值

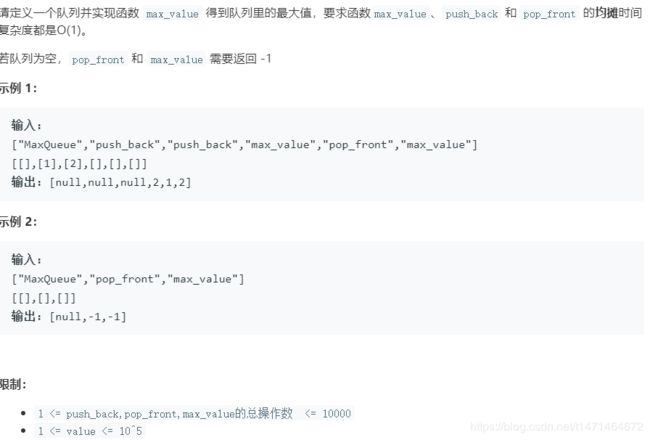
class MaxQueue:
    def __init__(self):
        self.queue=[]
        #用滑动窗口维持队列最大值，保证滑动窗口左端是当前队列中最大值，维持一个递减状态
        self.window=[]
    def max_value(self) -> int:
        if not self.queue:
            return -1
        return self.window[0]
    def push_back(self, value: int) -> None:
        self.queue.append(value)
        while self.window and self.window[-1]<value:
            self.window.pop()
        self.window.append(value)

    def pop_front(self) -> int:
        if not self.queue:
            return -1
        else:
            if self.queue[0]==self.window[0]:
                self.window.pop(0)
            return self.queue.pop(0)

1423. 可获得的最大点数


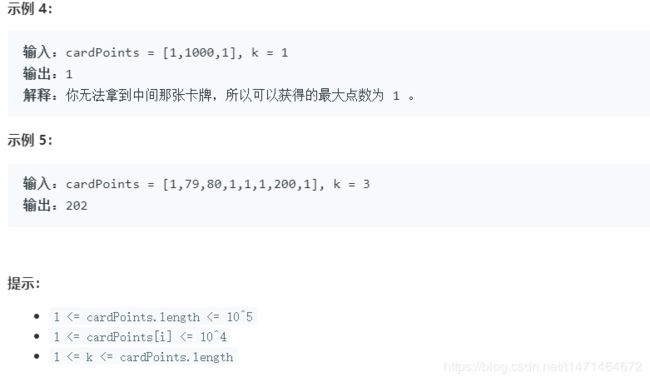
从两端取卡牌，使点数最大，那么从中间找长度为len(cardpoints)-k的窗口，点数和最小的连续子数组，最后用输入数组的和减去这个最小值就是结果

class Solution:
    def maxScore(self, cardPoints: List[int], k: int) -> int:
        if len(cardPoints)<=k:
            return sum(cardPoints)
        l=0
        n=len(cardPoints)
        res=float('inf')
        ans=0
        #窗口长度，保证窗口内和最小，窗口之外的卡牌就是需要取走的卡牌
        m=n-k
        # window=deque()
        for r in range(n):
            ans+=cardPoints[r]
            while l<r and r-l+1>m:
                ans-=cardPoints[l]
                # window.popleft()
                l+=1
            if r-l+1==m:
                res=min(res,ans)
            # window.append(r)
        return sum(cardPoints)-res

面试题 17.18. 最短超串(滑动窗口）

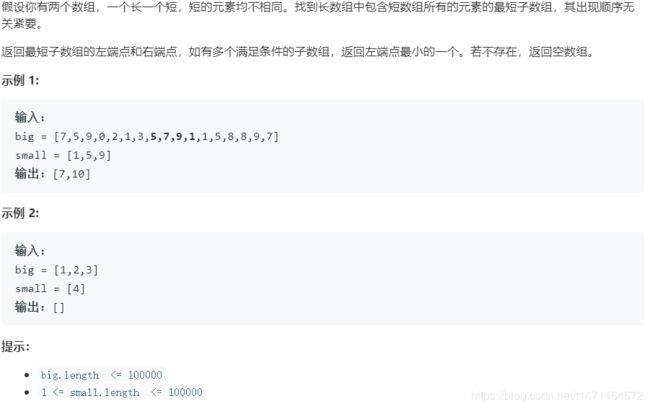
from collections import Counter
class Solution:
    def shortestSeq(self, big: List[int], small: List[int]) -> List[int]:
        hash1=Counter(small)
        hash2=defaultdict(int)
        k=len(small)
        l=0
        minl=float('inf'),None,None
        match=0
        for r in range(len(big)):
            hash2[big[r]]+=1
            if hash2[big[r]]==hash1[big[r]]:
                match+=1
            while match==k and l<=r:
                if minl[0]>r-l+1:
                    minl=(r-l+1,l,r)
                hash2[big[l]]-=1
                if hash2[big[l]]<hash1[big[l]]:
                    match-=1
                l+=1
        # if 0:--False
        return [minl[1],minl[2]] if minl[1]!=None and minl[2] !=None else []

1209 删除字符串中的所有相邻重复项 II


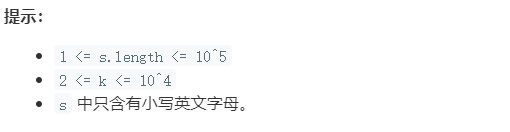
将计数器和元素存储栈中，根据栈中结果重构字符串
如果当前元素与栈顶元素相同，则栈顶元素计数器加1
如果当前元素与栈顶元素不同，则计数器置1，数据和计数器同时压入栈
如果栈顶元素计数器等于k，则弹出栈顶元素

class Solution:
    def removeDuplicates(self, s: str, k: int) -> str:
        if len(s)<k:
            return s
        stack=[]
        for i in range(len(s)):
            #遍历每个元素，判断与栈顶元素是否一致，如果不一致则压入栈，一致则栈顶元素计数加1
            if not stack or stack[-1][1]!=s[i]:
                stack.append([1,s[i]])
            else:
                stack[-1][0]+=1
                if stack[-1][0]==k:
                    stack.pop()
        res=''
        for i,j in stack:
            res+=j*i
        return res

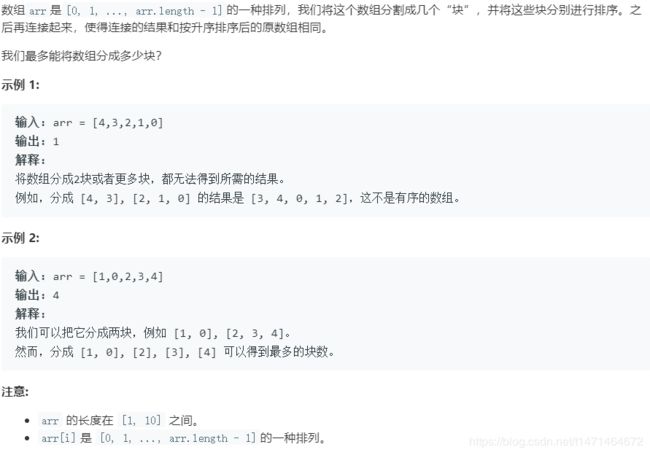
768. 最多能完成排序的块 II

分成块的前提是前一块的最大值，小于等于后一块的最小值
单调栈：
维护一个单调递增栈，单调栈的元素个数实际上是遍历到当前数字之前可以拆分成的块儿的个数，我们遇到一个大于栈顶的元素，就将其压入栈，说明在这个位置是可以拆分成块的
但是一旦后面遇到小的数字了，我们就要反过来检查前面的数字，有可能我们之前认为的可以拆分成块儿的地方，现在就不能拆，因为当前元素这个小的值，可能小于前面块的最大值

class Solution:
    def maxChunksToSorted(self, arr: List[int]) -> int:
        stack=[]
        for i in range(len(arr)):
            #维护单调递增栈
            if not stack or stack[-1]<=arr[i]:
                stack.append(arr[i])
            else:
                #栈内保存的是分割的每一块的最大值，要小于下一块的最小值
                cur=stack.pop()
                while stack and stack[-1]>arr[i]:
                    stack.pop()
                stack.append(cur)
        return len(stack)

哈希表法：
排序后的数组和未排序的数组，如果具有相同长度且元素一致，排列可能不一致，说明是一个块

class Solution:
    def maxChunksToSorted(self, arr: List[int]) -> int:
        rra=sorted(arr)
        ans=0
        hash1=defaultdict(int)
        hash2=defaultdict(int)
        for i in range(len(arr)):
            hash1[arr[i]]+=1
            hash2[rra[i]]+=1
            #对于可分的块需要满足，在原数组和排序后数组对应的位置，长度和元素一致，排列顺序可能不一致
            if hash1==hash2:
                ans+=1
                #清不清零都可以
                hash1=defaultdict(int)
                hash2=defaultdict(int)
        return ans

排序+累加和

class Solution:
    def maxChunksToSorted(self, arr: List[int]) -> int:
        rra=sorted(arr)
        sum1=0
        sum2=0
        ans=0
        for i in range(len(arr)):
            sum1+=arr[i]
            sum2+=rra[i]
            if sum1==sum2:
                ans+=1
        return ans

769. 最多能完成排序的块

class Solution:
    def maxChunksToSorted(self, arr: List[int]) -> int:
        stack=[]
        for num in arr:
            if not stack or stack[-1]<=num:
                stack.append(num)
            else:
                cur=stack.pop()
                while stack and stack[-1]>num:
                    stack.pop()
                stack.append(cur)
        return len(stack)

1371. 每个元音包含偶数次的最长子字符串

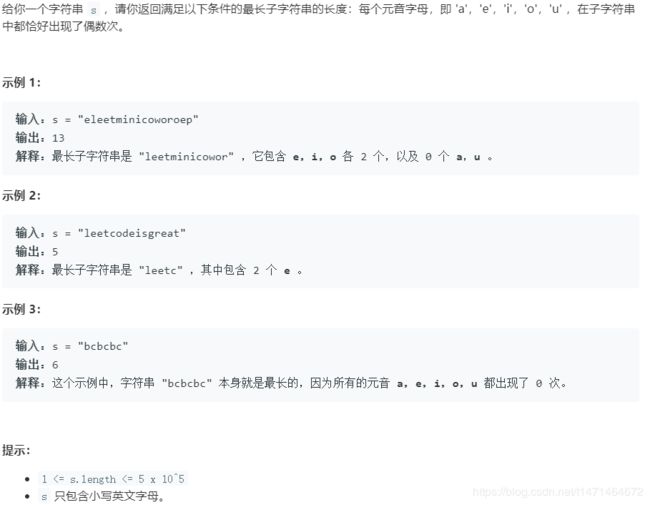
滑动窗口不可行，因为窗口长度可变，因为要求奇偶性，而不是类似“元音出现最多的子串”等。每次都应该从头遍历，滑动窗口不可行
暴力法：
对于每个子串，统计元音出现个数，符合条件则更新答案
枚举子串时，每次都从最长子串开始计算，找到一个满足条件就可以直接返回，不需要维护最大值

class Solution:
    def findTheLongestSubstring(self, s: str) -> int:
        #i是子串的长度，j是子串起点，从最长子串开始遍历，如果符合条件可以直接返回结果
        for i in range(len(s),0,-1):
            for j in range(len(s)-i+1):
                sub=s[j:i+j]
                flag=False
                for vowel in ['a','e','i','o','u']:
                    if sub.count(vowel)%2!=0:
                        flag=True
                        break
                if not flag:
                    return i
        return 0

前缀和：
前缀和简单理解为数列前N项的和
二维前缀和常用于求某个子矩阵的元素和
其实每个子串对应着一个区间，那么有什么方法可以在不重复遍历子串的前提下，快速求出这个区间里元音字母出现的次数呢？答案就是前缀和，对于一个区间，我们可以用两个前缀和的差值，得到其中某个字母的出现次数。
我们对每个元音字母维护一个前缀和，定义pre[i][k] 表示在字符串前 i个字符中，第 k 个元音字母一共出现的次数。假设我们需要求出 [l,r] 这个区间的子串是否满足条件，那么我们可以用 pre[r][k]−pre[l−1][k]，在 O(1)的时间得到第 k个元音字母出现的次数。对于每一个元音字母，我们都判断一下其是否出现偶数次即可。
我们需要枚举字符串的每个位置 i ，计算以它结尾的满足条件的最长字符串长度，其实我们要做的就是快速找到最小的j∈[0,i)，满足 pre[i][k]−pre[j][k]（即每一个元音字母出现的次数）均为偶数，那么以 i结尾的最长字符串 s[j+1,i] 长度就是 i−j。
偶数：对于满足条件的子串而言，两个前缀和 pre[i][k]和 pre[j][k]的奇偶性一定是相同的，这样我们只要实时维护每个元音字母出现的奇偶性，那么 s[j+1,i]满足条件当且仅当对于所有的 k，pre[i][k] 和 pre[j][k] 的奇偶性都相等，此时我们就可以利用哈希表存储每一种奇偶性（即考虑所有的元音字母）对应最早出现的位置，边遍历边更新答案
没理解

class Solution:
    i_mapper = {
        "a": 0,
        "e": 1,
        "i": 2,
        "o": 3,
        "u": 4
    }
    def check(self, s, pre, l, r):
        for i in range(5):
            if s[l] in self.i_mapper and i == self.i_mapper[s[l]]: cnt = 1
            else: cnt = 0
            if (pre[r][i] - pre[l][i] + cnt) % 2 != 0: return False
        return True
    def findTheLongestSubstring(self, s: str) -> int:
        n = len(s)

        pre = [[0] * 5 for _ in range(n)]

        # pre
        for i in range(n):
            for j in range(5):
                if s[i] in self.i_mapper and self.i_mapper[s[i]] == j:
                    pre[i][j] = pre[i - 1][j] + 1
                else:
                    pre[i][j] = pre[i - 1][j]
        for i in range(n - 1, -1, -1):
            for j in range(n - i):
                if self.check(s, pre, j, i + j):
                    return i + 1
        return 0

作者：fe-lucifer
链接：https://leetcode-cn.com/problems/find-the-longest-substring-containing-vowels-in-even-counts/solution/qian-zhui-he-zhuang-tai-ya-suo-pythonjava-by-fe-lu/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

918. 环形子数组的最大和


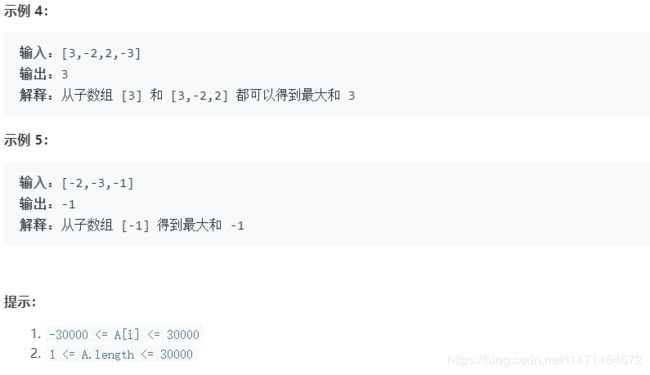
计算B=A+A的前缀和，Pk =B[0]+B[1]+⋯+B[k−1]，考虑最大的Pj-Pi ,其中j-i<=N(不超过数组长度，因为每个元素最多出现一次）
对于固定的j,**使Pj-Pi最大，那么找到使Pi最小的i,**且满足j-N<=iPj,就不用考虑这个i了
前缀和+优先队列

class Solution:
    def maxSubarraySumCircular(self, A: List[int]) -> int:
        #构造前缀和数组
        p=[0]
        for _ in range(2):
            for i in A:
                p.append(i+p[-1])
        n=len(A)
        #维持一个单调递增的优先队列，队列保存每个前缀和的下标，当下标i
        #队列头部保存着对当前j来说，最小的前缀和所处的下标
        queue=deque()
        queue.append(0)
        ans=float('-inf')
        for j in range(1,len(p)):
            if queue[0]<j-n:
                queue.popleft()
            ans=max(ans,p[j]-p[queue[0]])
            while queue and p[queue[-1]]>=p[j]:
                queue.pop()
            queue.append(j)
        return ans

遇到求数组子序列的极大、极小值问题，首先应该想到的是前缀和，将问题转换成求S[i] - S[j]的问题；