有限扩散集团凝聚模型（DLCA）第三讲：流动水流中的凝聚模拟(1)

上几节课我们都再讲这个模型在一个非常非常小的一个立方体中，然后这群粒子在里面走碰粘沉。在现实世界中，水不可能就在一个小立方体中，而且水是动态的、流动的。而DLCA模型讲的确实在静止的水中切一小块出来做分析，我们不能直接拿来用，于是本人结合另外一个“污染物在水中扩散的模型”来更真实的模拟胶体的絮凝过程。

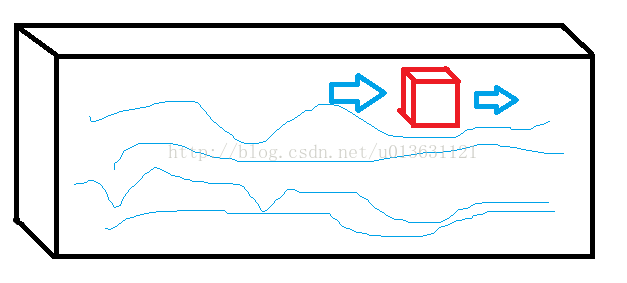
我们这次要做的，当然就是在流动水中，如图1所示，让这些粒子走碰粘沉，先做几个假定，首先我们这个这个流动的水是紊流状态，即Re>2000。其次，水具有自净化的能力（水中有一堆微生物之类的东西，能把胶体给吃了）。

 

图1

我们假设在t时刻点(x,y,z)的污染物的浓度为C(x,y,z,t)，C随着t的变化，即使是同一个点，值也是不同的。为什么不同呢，那就是因为水一流动，污染物就开始在水中扩散了，若污染物的扩散速度为D(Dx,Dy,Dz)，那么可以计算出某一个区域的污染物质量。

于是我们将这个河流个切割出一个小块，如图2，这个红色的小块中的污染物质量怎么算呢，现在假定时间是t~t+t1之间，通过流入的质量是M1，河流流动使得流出的质量是M2，水体自净去除的质量是M3，若t时刻的胶体一共重M，那么t+t1时刻的质量就为：M=M+M1-M2-M3。

 图2

下面，我们说一下M1、M2、M3是如何计算的

（1）流入红色小块中的质量M1，长宽高都是L（L足够小，使得L范围内的浓度近乎相同），上文提到了扩散速度D，它是x,y,z三个方向流入的，首先我们确定单位D的单位是m2/s，浓度的单位是mg/m3，那么从t~t+t1时刻(t1足够小,使得在t1时刻左右的浓度近乎相同Ct=Ct+t1）的M1为：

M1=t1*(Dx*Ct/L+Dy*Ct/L+Dz*Ct/L)

=Ct*t1*(Dx+Dy+Dz)/L

（2）流出小红块的质量M2：因为水流是在流动的，假设它的流速是u=(ux,uy,yz)，单位是m/s，那么它的质量M2很简单即可求出。

M2=ux*Ct*L*L+uy*Ct*L*L+uz*Ct*L*L

=L^2*Ct*t1*(ux+uy+uz)

（3）自己降解的质量M3：假设讲解的速率为K，单位是/s，那么很显然，M3的计算方法为：

M3=K*L*L*L*Ct*t1

=K*L^3*Ct*t1

（4）隐藏属性M4：但是，我们刚才说过了，我们假定Ct=Ct+t1，可是呢，无论多小的时间，浓度总是有变化的，我们一定得需要用一个M4给他补充上去，这个M4可不是M4A1全自动步枪啊，哈哈。补充的方式为：

M4=[Ct-C(t+t1)]*L^3

=M1-M2-M3

为什么为M4=M1-M2-M3呢，这是因为质量守恒，补充上去的质量哪来的，不就是流入的质量剪掉流出的和自净的质量的到的嘛。

我们知道了这些，下一步就是往水里面的某一个点上面投加污染物了，为了使得这个东西比较真实，我们在图1的左上角开始投加，投加之后，我们每过一段时间，比如0.0001秒，然后让它进行一次DLCA操作，之后让水流流动0.0001秒，然后再进行一次DLCA絮凝操作。以此类推，慢慢的，在整个水中就会形成一个絮凝效果了。

可是这时候有人问了，流动和絮凝是同时进行的啊，你这走一下，絮凝一次，不对啊。没错，是不对，但是毕竟我们这个是模拟呀，你想想0.0001秒絮凝一下，然后流动一下，时间这么短，这个和同时进行有区别吗？如果是0.00001、0.00000001、0.0000000001秒。。。如果时间无限短的话那不就是同步了嘛。

大家还有人会问，河流可不是立方体吧，外一是弯弯曲曲的怎么办呢，但这个教程我觉得我今天讲到这里就可以了，大家消化一下，下次课程将讲解，如何投药，以及曲面积分求解不规则河流过程。

 

 

 

参考文献：

[1] 卓金武, 李必文,魏永生,等. MATLAB在数学建模中的应用[M].北京航空航天大学出版社, 2014.

[2] 郭航. 水中絮凝体分形成长动态仿真技术研究[D].哈尔滨工业大学, 2012.

[3] 陈彦光, 刘继生.区域交通网络分形的DBM特征——交通网络Laplacian分形性质的实证研究[J].地理科学, 1999, 19(2):114-118.