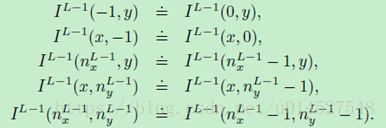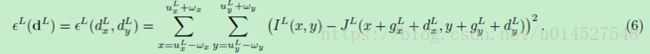金字塔Lucas Kanada特征（光流）跟踪算法 ——翻译/学习-笔记（1）

源论文：Pyramidal Implementation of theLucas Kanade Feature Tracker Description of the algorithm

1.   问题描述

I和J分别表示两幅灰度图。I(x) = I(x, y) 和J(x) = J(x, y)分别是两幅图像上位置为[x, y]^T处像素点x的灰度值，x和y分别为该点的像素坐标。令I为第一幅图像，J为第二幅图像。在实际中，图像I和J分别是离散化函数或者矩阵，左上角的像素坐标为[0, 0]^T。n­­_x和n_y表示两幅图像的宽和高，基于左上角的像素坐标可以得到右下的像素坐标为[n_x-1, n_y-1]^T。

对于第一幅图像上的图像点u = [u_x,u_y]^T, 特征跟踪的目的便是在第二幅图像上找到使得I(u)和J(v)相似的点v = u + d = [u_x+d_x, u_y+d_y]^T的具体位置。向量d = [d_x, d_y]^T为图像在x点处的速度（准确来讲，应该是位移），也称为x点处的光流。因为孔径问题的存在，需要在一个2D邻域去定义相似关系。 ω_x和ω_y分别为两个整数，定义以图像位移d为向量的最小化误差函数为：

由上面函数可见，度量相似性的误差函数基于图像中大小为（2ω_x+1）*（2ω_y+1）的邻域块进行测量。此邻域也称为集成窗口，ω_x和ω_y一般取2,3,4,5,6,7个像素大小。

2.   跟踪算法

对于任何一个关键点跟踪，其有两个衡量指标：精度和鲁棒性。精度和负责跟踪的局部子像素位置精度有关。很明显，为了不平滑掉图像的细节信息，小的集成窗口更加适合，也就是小的ω_x和ω_y 取值（因为窗口越大，特征点附近的细节信息越会被平滑稀释掉）。在图像中的阻塞区域尤其要求比较小的窗口，因为那里可能不同点在两个路径中移动的速度不同（空间点和相机间的距离不同，相同的相机运动下像素点移动的速度和位移也不同）。

鲁棒性和不同的光度、图像运动的下追踪的敏感度有关。尤其是，为了处理大幅的运动，直观上选择一个大的集成窗口显然更有优势。确实，如等式（1）所示，令d_x≤ω_x且d_y≤ω_y是一种更加合适的参数选择方法（除非有可用的先验匹配信息）。所以说，选择集成窗口大小的时候，在局部精度和鲁棒性间的需要有一个权衡。为了解决这个问题，论文作者提出了一种基于经典Lucas-Kanade算法的金字塔实现方法。还利用迭代LK光流计算方法实现了更高的局部跟踪精度。

2.1   图像金字塔的建立

大小为n_x*n_y的图像I的金字塔结构可通过下面方法建立：I⁰=I表示第0^th层的图像，此图像的分辨率最高（原始图像），其宽度和高度也和原始图像一致n⁰_x­=n_x,n⁰_y­=n_y。接着，金字塔结构以一种递归的方式建立：基于I⁰计算I¹，接着基于I¹计算I²…。令L=1,2…作为金字塔的其中一层，令I^L-1表示在L-1层的图像。n_x^(L-1)和n_y^(L-1)分别为I^(L-1)的宽度和高度。图像I^L-1的灰度值可以由下式进行计算：

简单起见，基于下列各式计算图像I^L-1中边缘附近的像素点值：

由等式2可见，2x和2y的范围为[0, n_x^(L-1)-1]和[0, n_y^(L-1)-1 ]。所以，I^L图像的宽度和高度分别需要满足下面约束：

基于等式（2）、（3）和（4）递归地构建I和J两幅图像的金字塔结构（L=0…L_m）。L_m为金字塔的高度（可以自己根据需要选择）。比如：大小为640*480的图像I，其I¹、I²、I³和I⁴大小分别为320*240、160*120、80*60和40*30。大部分情况下金字塔高于4层没太大意义。金字塔结构主要是为了解决大像素运动，也就是比集成窗口还大的运动。所以金字塔的高度也需要根据实际中光流运动的最大值去选择。等式（2）中建议在二次采样之前利用低通滤波器[1/4 1/2 1/4]*[1/41/2 1/4]^T对图像进行抗锯齿操作。在实际中（比如C代码中），建立金字塔时会采用更大的一个抗锯齿滤波器[1/16 1/43/8 1/4 1/16] * [1/16 1/4 3/8 1/4 1/16]^T。

2.2   金字塔特征跟踪

特征跟踪的目的是：对于一个给定的图像I中的点u，找到图像J中与之对应的位置v=u+d，或者是找到该点的像素位移向量d（参见等式（1））。

对于L=0…L­_m，定义金字塔图像I^L中点u对应的坐标u^L=[u^L_{x ，}u^L_y]。基于上一部分中等式（2）、（3）和（4），可得向量u^L可以通过下式计算：

上述的除法操作独立应用于每一层金字塔图像的的坐标计算中（子等式中就是连乘的操作）。当L=0时，可见u⁰=u。

金字塔跟踪算法的整体处理流程如下：首先，在最顶层L_m计算光流；接着，基于上一层计算的结果得到L_m-1层像素位移的初始估计值。基于此初始估计值，在L_m-1层计算定义的光流，而且接着此结果被传递到下一层L_m-2，依次传递知道第0层（也就是原始图像）。

下面用数学公式描述L+1和L层间的递推关系。假设在L层的初始光流位移估计值为g^L=[g^L_x, g^L_y]^T，该估计值从顶层L_m一直递推到上一层L+1。接着，为了计算L层的光流，通过对这层的图像建立最小化误差匹配函数求解残余像素位移d^L=[d^L_x, d^L_y]^T（相当于在上一层的位移基础上进一步求解更加精确的像素位移，最终的位移需要累加顶层到底层的位移）:

所有L层的集成窗口大小均为（2 +1）*（2 +1）。每一层中的光流初始位移估计值g^L在图像J中可以对像素的移动路径进行预移动（相当于移动路径的预处理）。这样的话，光流的残余位移向量d^L=[d^L_x , d^L_y]^T会是一个比较小的量，这样可以更加容易的利用标准的LK方法进行计算。

残余光流位移d^L的计算在下一部分详述，先假设这个向量d^L已经被计算过了。接着，L层的计算结果d^L会通过下一层的初始位移估计值g^L-1被传递到L-1层，表达式如下：

最终的光流移动计算结果d（参考等式（1））可通过金字塔最底层的图像（L=0）计算得到：

上式也可以进一步写为：

金字塔结构的明显优势在于对于一个比较大的像素位移L，可以将其逐步分解为多个比较小的残余光流位移d^L进行计算。假设每一次基本的光流计算可以处理的最大像素运动是d_max，那么基于金字塔结构可以处理的整个像素运动最大值为d_{max_final}=（2^Lm+1-1）dmax。每多加一层结构L，就要多加下一层L-1最大处理像素运动位移的两倍。最终可以处理的最大像素运动位移是所有层可处理的最大运动的累加值。这个可以通过下面的表格理解：

层数	该层可处理的最大位移	该金字塔结构可处理的最大位移	倍数/增益（与非金字塔结构算法相比）
L0	dmax	dmax	1
L1	2dmax	L0+L1=3dmax	3
L2	4dmax	L0+L1+L2=7dmax	7
L4	8dmax	L0+L1+L2+L3=15dmax	15

也就是说，如果金字塔的高度为3，即L_m=3，则金字塔LK光流跟踪算法可处理的最大像素运动位移是标准LK光流跟踪算法可处理最大位移的15倍。这能够在不增大集成窗口大小的情况下，有效处理大幅的像素运动，这样较好的兼容了特征跟踪鲁棒性和精度。