关于逻辑回归的思考

关于逻辑回归的思考

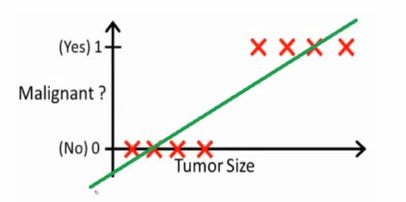
1.问题的引出

问题是：

• 如果出现断崖式的变化，线性拟合的效果就不是很好。
• 可能需要一个会产生阶跃且连续的函数来进行拟合

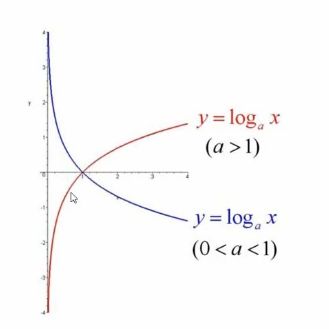
2.sigmod函数

$$g(z)=\frac{1}{1+e^{-z}}=\frac{e^z}{1+e^z}$$

• 自变量$z$的范围是$(-\infty ,+\infty )$，值域的范围$g$是$(0,1)$
• 一个很自然的想法就是，以某一个函数$z$作为$g$的输入，再将$g$对应的输出作为概率输出，通过设定阈值，将结果进行分类（二分类，（0-1））。
• 那么关于数据$\mathbf{x}$（或$\mathbf{X}$）,先构造什么样的$z$呢？答案是任意，只要是能够符合数据的就是合理的。所以$z$的选取不是固定的！

例1

• 这个分类自然想到线性模型

  • 令$z={\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2$

    • 当$z=0$时，即${\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2=0$时，恰好对应一条直线

      

    • 对于要分类的点，均在直线两侧，那么将他们的坐标带入$z$中的结果是$z>0$或$z<0$（二者区其一）。

    • 问题是$sigmod函数$如何对其起作用呢？答案是通过将点带入$z$中，对于此时$z$的输出（$>0$或$<0$）进行设定阈值。根据$sigmod函数$的特性，自然可以想到将$0.5$作为阈值。

      • 当$x$在$z$的作用下输出结果$result>0$，$result$再在$sigmod函数$作用下，输出结果$>0.5$，此时判定为类别1
      • 当$x$在$z$的作用下输出结果$result<0$，$result$再在$sigmod函数$作用下，输出结果$<0.5$，此时判定为类别0

• 大致的设计思路:

  1. $z={\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2$
  2. $g(z)=\frac{1}{1+e^{-z}}$
  3. 通过$g$的输出和设定的阈值进行比较，得出分类结果。
     • 上述未知的量时参数$\Theta$，这个才怎么求呢？下面再说。

例2

• 这个自然想到一个分类边界是圆（分非线性模型）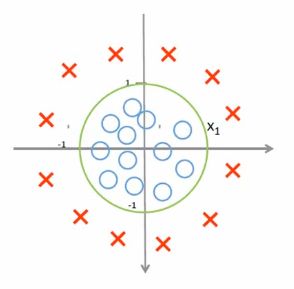
• 
  • 令$z={\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2+{\theta }_3\ast x_1^2+{\theta }_4\ast x_4^2$。（这里不需要$x_1\ast x_2$的交叉项）
    • 令$z=0$，此时正是圆的边界。对于要分类的点带入$z$中，输出结果$>0$或$<0$（二者取其一）
    • 以后的分析和上述例1相同。（$sigmod函数$的作用，阈值的选取等，均一致）
• 大致的设计思路:
  1. $z={\theta }_0+{\theta }_1\ast x_1+{\theta }_2\ast x_2+{\theta }_3\ast x_1^2+{\theta }_4\ast x_4^2$
  2. $g(z)=\frac{1}{1+e^{-z}}$
  3. 通过$g$的输出和设定的阈值进行比较，得出分类结果。
     • 上述未知的量时参数$\Theta$，这个才怎么求呢？下面再说。

对比发现

• 对于上述例1和例2的比较，逻辑回归的整体设计思路大致相同。要解决的两个问题是：
  1. 如何确定一开始的$z$？，从结果上看，线性模型和非线性模型均可。并没有定法，这个$z$的选取得结合具体的$X$分布进行选择。
     • 注：$X$的分布在高维的时候判定本身就是一个难题，所以$z$的确定也不是一件容易的事情。
  2. 假定已经确定了$z$的函数表达（但其中的参数$\Theta$未知），该如何求参数$\Theta$？
     • 求参数的方法，基本上会针对目标函数（损失含糊）采用迭代法（解析解太困难了，有时候甚至不可行）
     • ==问题又变成了：针对$sigmod函数 $找一个什么样的目标函数（损失函数）？==这就是下面要说的事了！

逻辑回归是如何做到分类的？

• 针对逻辑回归，其中的$sigmod函数$和对应的损失函数的确定，是该方法的精髓。

1.模型

假定已知$函数z_{\theta }(x)$，那么将其作为$gidmod函数$的输入，$g(z)$。那么有一个假设空间$h_{\theta }(x)$。
$$已知z_{\theta }(x);g(z)=\frac{1}{1+e^{-z}}$$

$$h_{\theta }(x)=g(z_{\theta }(x))=\frac{1}{1+e^{z_{\theta }(x)}}$$

其中：$h_{\theta }(x)\in (0,1)$。这个是设计损失函数的关键。

2.策略

损失函数

1. 对于一个样本损失
   $$cost(h_{\theta (x)},y)=\{\begin{array}{l}-log(h_{\theta }(x)),y=1\\ -log(1-h_{\theta }(x)),y=0\end{array}$$

   • 解释：
     • 在已知分类信息$y=1$时，希望$h_{\theta }(x)$的值越接近1最好，这样损失才更小。假设，在$y=1$时，但是分类错了，即$h_{\theta }(x)$的值相对来说可能更接近于0（从右侧趋近于0），此时$-log(h_{\theta }(x))$的值会变大，意味着损失增大，而目标就是来最小化这个损失。所有此时针对一个样本在$y=1$时设计的损失函数是合理的。
     • 在已知分类信息$y=0$时，希望$h_{\theta }(x)$的值越接近0最好，这样损失$-log(1-h_{\theta }(x))$才更小。假设，在$y=0$时，但是分类错了，即$h_{\theta }(x)$的值相对来说可能更接近于1（从左侧趋近1），此时$-log(1-h_{\theta }(x))$的值会变大，意味着损失增大，而目标就是来最小化这个损失。所有此时针对一个样本在$y=0$时设计的损失函数是合理的。
     • 但是上述的算是有一个问题，那就它是分段函数，不利于优化，所以有了下面的合并。

2. 技巧上的合并（背后有最大熵理论模型，对数最大似然估计）
   $$cost(h_{\theta }(x^{(i)},y^{(i)})=-(y^{(i)}\ast log(h_{\theta }^{(x^{(i)})}+(1-j^{(i)})\ast log(1-h_{\theta }^{x^{(i)}})$$

3. 损失函数：

   1. 经验风险
      $$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\ast log(h_{\theta }^{(x^{(i)})}+(1-j^{(i)})\ast log(1-h_{\theta }^{x^{(i)}})$$

   2. 结构风险
      $$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\ast log(h_{\theta }^{(x^{(i)})}+(1-j^{(i)})\ast log(1-h_{\theta }^{x^{(i)}})+\lambda \sum _{j=0}^n{\theta }_j^2$$

3.算法

对于$g(z)=\frac{1}{1+e^{-z}}$的求导，
$$\begin{gathered} \frac{d(g(z))}{dz}=-(1+e^{-z}{)}^{-2}\ast e^{-z}\ast (-1) \\ =\frac{1}{1+e^{-z}}\ast \frac{e^{-z}}{1+e^{-z}} \\ =\frac{1}{1+e^{-z}}\ast (1-\frac{1}{1+e^{-z}}) \\ =g(z)\ast (1-g(z)) \end{gathered}$$
所以
$$\begin{gathered} \frac{\partial g}{\partial {\theta }_j}=\frac{\partial g}{\partial z}\frac{\partial z}{\partial {\theta }_j} \\ =g(z)\ast (1-g(z))\ast \frac{\partial z}{\partial {\theta }_j} \end{gathered}$$
特别地，当$z_{\theta }(x^{(i)}={\theta }^T{x}^{(i)}$，得到$\frac{\partial z}{{\theta }_j}=x_j^{(i)}$。

此时，
$$\frac{\partial g}{\partial {\theta }_j}=g(z)\ast (1-g(z))\ast \frac{\partial z}{\partial {\theta }_j}=g(z)\ast (1-g(z))\ast x_j^{(i)}$$

采用梯度下降算法求解参数$\Theta$

$${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta ),(j=0\cdots n)$$

$$\begin{gathered} \frac{\partial }{\partial {\theta }_j}J(\theta )=\frac{\partial }{\partial {\theta }_j}(-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\ast log(h_{\theta }^{(x^{(i)})}+(1-j^{(i)})\ast log(1-h_{\theta }^{x^{(i)}})) \\ \cdots \\ \cdots \\ =-\frac{1}{m}\sum _{i=1}^m(y^{(i)}-g({\theta }^T{x}^{(i)}))\ast x_j^{(i)} \end{gathered}$$

说明：

• 上述的计算并没有什么难度，有难度的地方主要有两点：

  1. 关于逻辑回归中的$sigmod函数$的使用和一个样本的损失函数的设计和最终的损失函数的设计（对数最大似然）。

  2. 采用标量进行求导或者求偏导，问题着实不大。转化成用矢量计算，会比标量下计算要难一点。

总结：

1. 逻辑回归可以将连续值通过$sigmod函数+阈值限定$转为离散值问题（二分类问题）
2. $sigmod函数$的使用
3. 对数最大似然函数
4. 矢量下求导

参见：
统计学习方法
机器学习实战
https://blog.csdn.net/qq_38923076/article/details/82925183