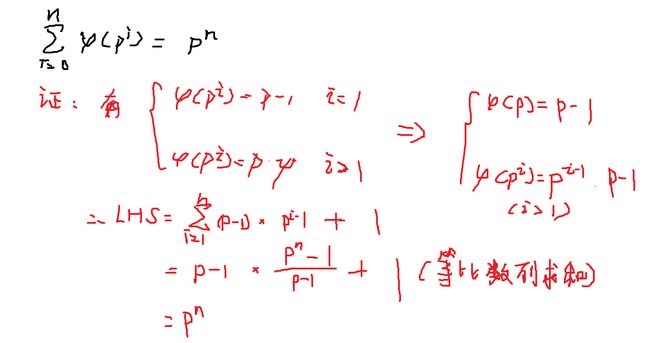对于一个整数\(a\),若\(b|a\)则称\(b\)是\(a\)的因数。
正因数求法
1、试除法
对于一个数\(n\),其正因数必定不会超过\(n\),所以只用枚举一下\(1-n\)的所有数看看它是不是\(n\)的因数即可。复杂度\(O(n)\)。
因为因数必定成对出现,所以只用枚举到\(\sqrt{n}\)即可。复杂度\(O(\sqrt{n})\)。
这样求\([1,n]\)中所有数的约数集合的时间复杂度为\(O(n\sqrt{n})\)。
for (int i = 1; i <= n; i++) {
for (int j = 1; j * j <= i; j++) {
if (i % j) continue;
fac[i].push_back(j);
if (j * j != i) fac[i].push_back(i / j);
}
}
2、倍数法
用来快速求\([1,n]\)中所有数的约数集合。
思想类似埃式筛法,用\(i\)去更新\(i\)的倍数。
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j += i) {
fac[j].push_back(i);
}
}
时间复杂度为调和级数:\(O(n\ln{n})\),同时说明\([1,n]\)的约数个数大约为\(n\ln{n}\)。
约数个数与约数和
将\(n\)质因数分解\(n=\Pi_{i=1}^{m} p_i^{c_i}\)可以得到\(n\)的约数集合\(\Pi_{i=1}^{m} p_i^{a_i}, a_i \in [0,c_i]\)。
即可得到约数和为\(\sigma(n)=\Pi_{i=1}^{m}\sum_{j=0}^{c_i}p_i^{j}\)。
约数个数为\(d(n)=\Pi_{i=1}^{m} (c_i+1)\)
最大公约数
对于两个数\(a,b\),如果\(d|a 且 d|b\)则称其为公约数,其中最大的称为最大公约数记作\(gcd(a,b)\)或\((a,b)\)。
最大公约数的性质:
1、\(gcd(a,b)=gcd(b,a)\)
2、\(a|b\)等价于\(gcd(a,b)=a\)。
3、\(gcd(a,1)=1, gcd(a,0)=a\)。
4、辗转相减法:\(gcd(a,b)=gcd(a,b-a)=gcd(a,a-b)\)。
5、\(gcd(ca, cb)=c \times gcd(a,b)\)。
6、\(gcd(a+cb, b)=gcd(a,b)\)。
7、若\(gcd(a,c)=1\)则\(gcd(a,bc)=gcd(a,b)\)
8、\(gcd(a,b,c)=gcd(gcd(a,b),c)\)。
9、若\(gcd(a,b)=1\)则\(gcd(ab,c)=gcd(a,c) \times gcd(b,c)\)。
10、若\(d\)是\(a,b\)的公约数,则\(gcd(a/d,b/d)=gcd(a,b)/d\)。
证明:
1、显然。
2、最大公约数不会超过两者中较小的一个(0是特例),得证。
3、一式由2即得证,二试所有数都是0的"约数"即得证。
4、设\(d=gcd(a,b),a=dm,b=dn\),有\(gcd(m,n)=1\),又有\(gcd(m,m-n)=1\)即得证。\(gcd(m,m-n)=1\)可由反证法得出。
5、显然。
6、由辗转相减法得证。
7、将a,b,c质因数分解即可得证。
8、设\(d=gcd(a,b,c),a=dr,b=ds,c=dt,gcd(r,s,t)=1\),\(d|gcd(a,b)\),可得\(gcd(a,b)\)与\(c\)的最大公约数即为\(d\)。
9、同7的方法。
10、类似5
欧几里得算法:\(gcd(a,b)=gcd(b,a\%b)\)。
证明:由辗转相减法得证。
int gcd(a,b) {return b == 0 ? a : gcd(b,a % b);}
最小公倍数
如果一个数\(c\)满足\(a|c且b|c\),则称\(c\)是\(a,b\)的公倍数,最小的\(c\)称为最小公倍数。
性质:
1、\(lcm(a,b)=lcm(b,a)\)。
2、\(lcm(a,1)=a, lcm(a,0)=0\)。
3、\(a|b\)->\(lcm(a,b)=b\)。
4、\(lcm(a,b,c)=lcm(lcm(a,b),c)\)。
5、\(lcm(ac,bc)=c \times lcm(a,b)\)
6、\(d|a且d|b\),\(lcm(d/a,d/b)=lcm(a,b)/d\)。
7、\(gcd(a,b) \times lcm(a,b)=a \times b\)。
主要证明性质7(也是主要用来求lcm的方法)。
设\(d=gcd(a,b)\),则\(a=dm,b=dn\),则\(lcm\)得是\(m,n,d\)的倍数又\((m,n)=1\)所以\(lcm(a,b)=dmn\)。
最大公因数与最小公倍数的唯一分解:
\(a=\Pi_{i=1}^{m} p_i^{a_i},b=\Pi_{i=1}^{m} p_i^{b_i}\)(没有的话指数就是0)。
则\(gcd(a,b)=\Pi_{i=1}^{m} p_i^{min(a_i,b_i)},lcm(a,b)=\Pi_{i=1}^{m} p_i^{max(a_i,b_i)}\)。
习题:hankson的趣味题
欧拉函数
记\([1,n]\)中与\(n\)互质的数的个数为\(\phi(n)\),即为欧拉函数。
求欧拉函数的公式:\(n \times \Pi_{i=1}^{m} \frac{p_i-1}{p_i}\)
用简单的容斥即可得证。
欧拉函数的性质:
\(gcd(a,b)=1 -> \phi(ab)=\phi(a) \times \phi(b)\)(积性函数的性质)
1~n中与\(n\)互质的数的和为\(\phi(n) \times \frac{n}{2}\)
对于质数\(p\)如果\(n\%p==0且n\%p^2!=0\)则\(\phi(n)=\phi(\frac{n}{p}) \times (p-1)\)(由积性函数的性质得证)
对于质数\(p\)如果\(n\%p==0且n\%p^2==0\)则\(\phi(n)=\phi(\frac{n}{p}) \times p\)(展开即可得证)
对于质数\(p\)有\(\sum_{i=0}^n \phi(p^i)=p^n\)
证明:
\(\sum_{d|n} \phi(d) = n\)
有关欧拉函数的应用:这篇博客写得不错