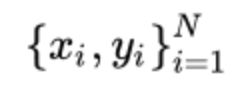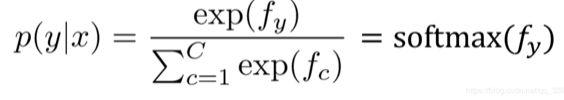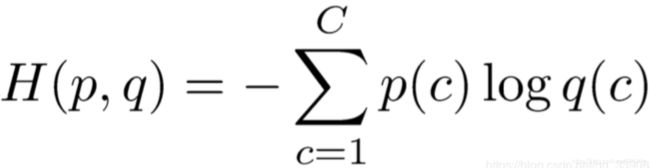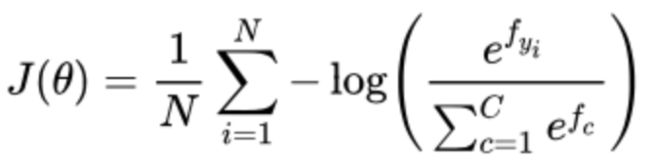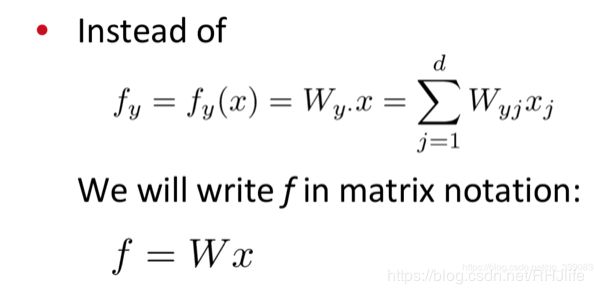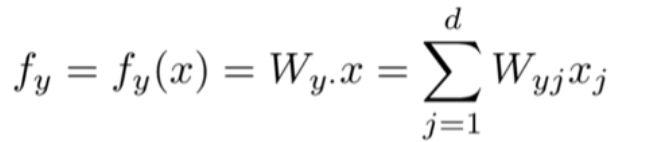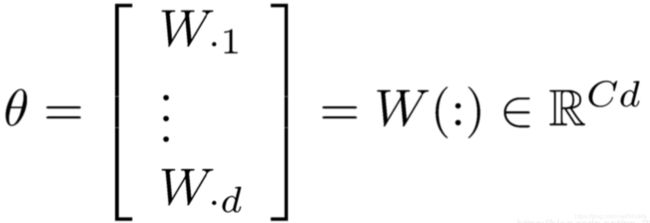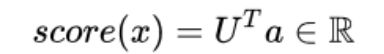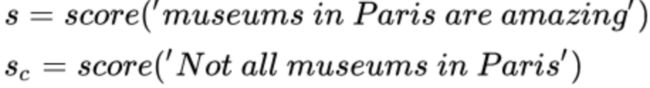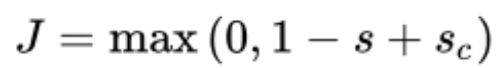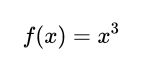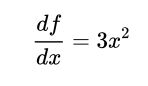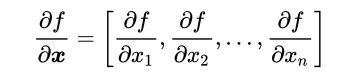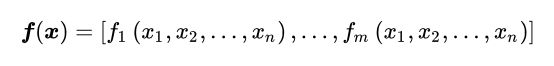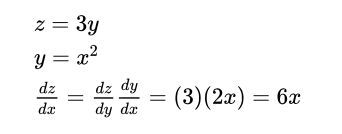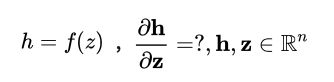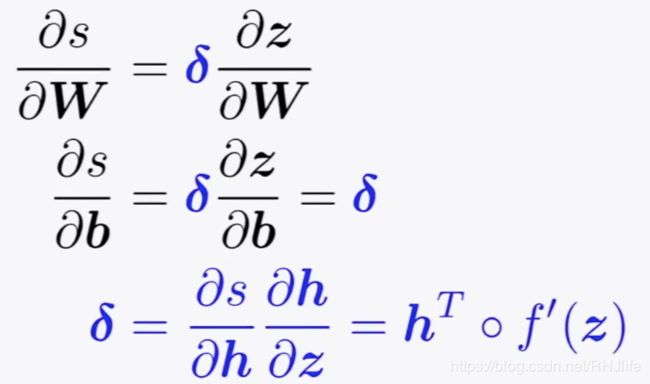2019年CS224N课程笔记-Lecture 3: Word Window Classification, Neural Networks, and Matrix Calculus
资源链接:https://www.bilibili.com/video/BV1r4411
正课内容
分类的介绍和概念
xi 是输入,例如单词、句子、文档(索引或是向量),维度为d
yi是我们尝试预测的标签( C个类别中的一个),例如:
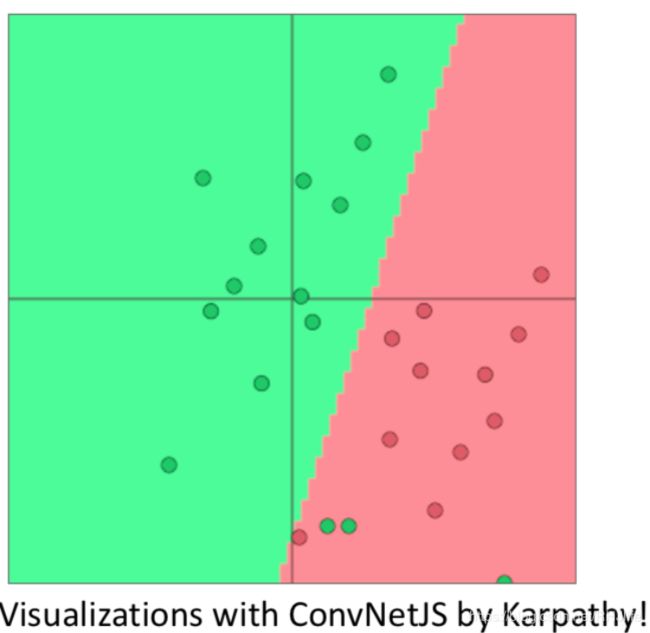
以一个简单样例为例:
对于上图的训练过程如下:
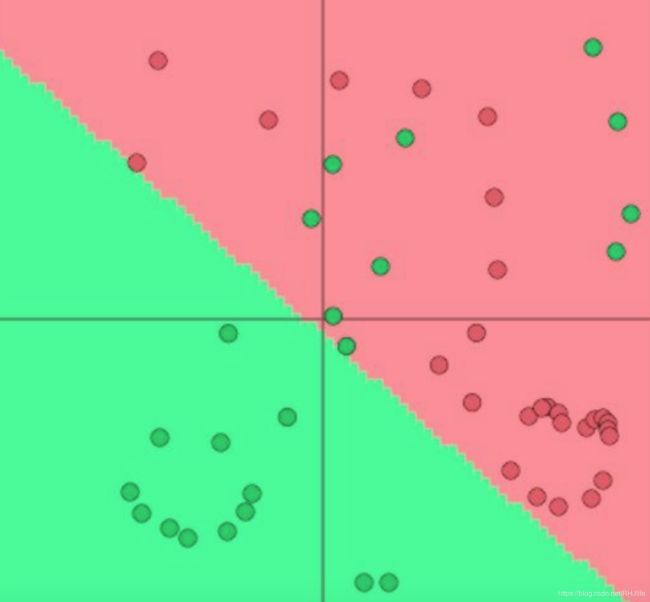
- 任务:固定的二维单词向量分类 (输入是单词向量(2维),输出是单词对应的类别标签,类似于y=ax1+bx2+c)
- 使用softmax/logistic回归进行分类
- 产生线性决策边界(绿色和红色的边界)
传统的方法/机器学习方法/统计学方法:假设xi是固定的,训练逻辑回归权重W来确定一个边界,官方一点就是假设 xi是固定的,使用 softmax/logistic 回归方法训练的权重 W∈R(R的维度:C×d)来决定决策边界(超平面)
具体过程如下:
目标函数
预测值计算
将权重矩阵W的第y行(类别y对应的权重)和输入(特征)向量 x做内积得到类别y对应的预测值:
使用softmax函数获得归一化的概率(当前输入x属于类别y的概率,当然,这是预测出来的概率)
损失函数
对于每个训练样本 (x,y) ,我们的目标是最大化正确类 y 的概率,或者我们可以最小化该类的负对数概率。
交叉熵损失函数
在整个数据集 上的交叉熵损失函数,是所有样本的交叉熵损失的均值
(原因是:上述两个式子其实是等价的,但是矢量计算更快~自己可以测试一下的)
(还有个问题~就是为什么选择交叉熵而不是平方差作为损失函数~这个可以自己了解下哟~)
传统的ML/机器学习的优化
参数θ为:
所以我们更新的梯度是:
神经网络
但是这个线性分类能力有限,不能处理复杂的分类。(因为它只能在空间上画一条直线)
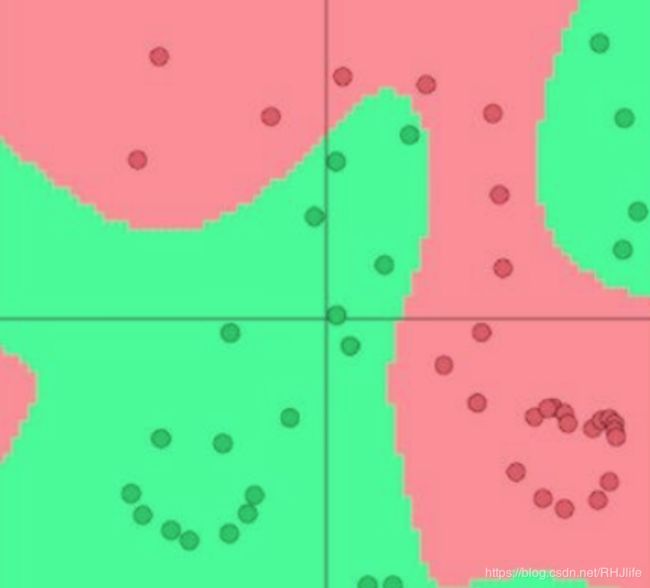
而神经网络则可以处理复杂的数据分布,如下图,线性分类是无法实现的。
我们想要的结果:(这个是可以通过神经网络来得到的,因为神经网络可以学习更复杂的函数和非线性决策边界)
非线性化函数(本章节说的是sigmoid函数,其实有很多的激活函数/非线性函数,例如relu和tanh)
一个神经网络往往由多个隐藏层构成~
(第一层是输入层,不进行计算,其他的隐藏层+输出层都是进行计算的)
对于一层来说:
为什么要引入非线形呢?或者说为什么需要激活函数/非线性化?
(这里的多层感知机就可以理解成视频中说的非线性的神经网络)
命名实体识别/NER
任务:例如标注文本中实体的名称/或者词性等 ,如图所示:
可能用途:
- 跟踪/识别文档中提到的特定实体(如组织名、人名、地点、歌曲名、电影名等)
- 对于问答,答案通常是命名实体
- 许多需要的信息实际上是命名实体之间的关联
- 同样的技术可以扩展到其他 slot-filling 槽填充分类(序列标注任务)
为什么命名体识别如此困难呢?
- 很难计算出实体的边界,例如有一段话,包含 “First National Bank” ,那么到底是“First National Bank”还是“ First”和“National Bank”呢?
- 很难知道是否某样东西是一个实体,例如“Future School” 是名字是“Future School” 的学校还是未来的学校?
- 很难识别出不知道的实体,例如“Balabalahong”是个人还是一段咒语?
- 上下文的不同导致某些词的意义不一样,例如jack是人名还是劫持,需要依赖上下文语境
还有一些其他的挑战例如:细粒度命名实体识别、嵌套命名实体识别、间隔命名实体识别等
Binary word window classification
一般情况下,分类单个单词是很困难的,因为会有一词多义等问题(上面也说了,实体会依赖上下文的~),所以往往采取窗口分类(以分类单词为中心选择一个窗口,在相邻单词的上下文窗口中对单词进行分类)
简单方法:在上下文中对单词进行分类的一个简单方法可能是对窗口中的单词向量进行平均,并对平均向量进行分类。问题:这会丢失位置信息
稍微好一点的方法:训练softmax分类器对(窗口)中心词进行分类(打实体标签),方法是在一个窗口内将中心词周围的词向量串联起来。如下图所示:
损失函数:(可以使用之前的,因为我们推到过softmax的loss了)
关于得分情况/预测值与实际值的比较:主要看中心词的预测结果和标注的结果是否准确
关于命名实体的位置:我们选择该窗口的中心词作为训练结果比较的对象,而不是其他窗口,例如:Not all museums in Paris are amazing,假设窗口为5,一个真正的窗口,以Paris为中心的窗口(museums in Paris are amazing)和所有其他窗口(它们的中心词不是位置实体,其他窗口很容易找到,而且有很多,例如Not all museums in Paris)
关于结果的计算:使用神经激活输出 a 简单地给出一个非标准化的分数
训练目标:
确保对的窗口的分数最大,corrupt窗口分数最小,例如:
单个窗口的目标函数:
窗口的中心词是位置实体时得分比窗口的中心词不是位置实体的得分高1分,要获得完整的目标函数:为每个真窗口采样几个其他(损坏)窗口。对采样的窗口和真实窗口进行求和,类似于负采样,然后更新参数。
计算梯度
以一个简单的例子为例:给定一个函数,有1个输出和1个输入
斜率即导数,如下:
样例稍微复杂一点:给定一个函数,有1个输出和 n 个输入 (输入是一个向量)
x向量的维度为n,所以对n维向量进行求导,也就是对向量中每个元素求偏导数,梯度的维度=1*n
再复杂一些:给定一个函数,有 m 个输出和 n 个输入
其雅可比矩阵是一个m×n的偏导矩阵(维度:输出*输入)
对于单变量复合函数:乘以导数
对于一次处理多个变量的复合函数:乘以雅可比矩阵:
带激活函数的样例:
由于权重矩阵i行乘以第i个元素,所以hi=f(zi)
函数有n个输出和n个输入 → n×n 的雅可比矩阵:
其他的一些求导: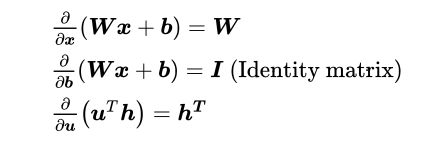
关于h矩阵是否要转置还有b是1还是1的向量(这个地方可以根据后面想乘的矩阵进行凑)
回到我们命名实体识别那一部分~
如何计算 s对b求导呢?
实际上,我们关心的是损失的梯度,但是为了简单起见,我们将计算分数的梯度.
做个等价变换
计算过程如下:
如何计算 s对w求导呢?
前两项/蓝色部分是重复的,无须重复计算:
其中,deltadelta 是局部误差符号,被称为误差信号和神经网络的沟通~.
(下节课将会介绍反向传播)
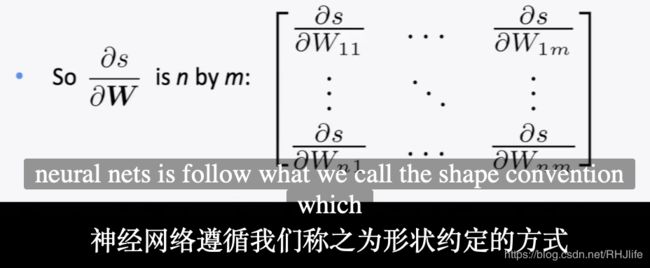
关于输出形状的介绍:
如果1个输出,n×m个输入,按照之前说的就是1 × nm 的雅可比矩阵,这显然不是我们想要的,所以对于上述讨论的问题,而是遵循惯例:导数/梯度的形状是参数的形状 (形状约定)
具体如下:
最后的形状如何确定呢?(我还是比较建议中间计算中...根据实际矩阵运算的需要去确定。其实实际开发中,类似tensoflow和pytorch等都提供自动求导~)