相机自动标定开发-第三阶段
简介
机器人的自我位置定位是一个基本而且重要的功能,是机器人自主导航的目标之一,是SLAM(实时定位和三维重建)的基础。我们工作室与深圳无人机公司的合作方向是——使用单片机,搭载摄像头、Wi-Fi、蓝牙等模块,向单片机移植视觉功能,使之具有自我三维定位和姿态测算的能力。
目前,定位功能有三种方法实现,惯性传感系统、激光测距系统和视觉系统。惯性传感系统使用加速度传感器、陀螺仪、罗盘等设备进行位移和旋转的测算;激光测距系统使用激光和时间测量进行距离测算;视觉使用相机,依靠拍摄的图片进行位置和旋转的测算,注意,这里所说的“视觉”特别指“单目视觉”,也就是仅使用一台摄像机的视觉方案。这三种方法各有优劣,我们这里不作比较,只关注视觉方案。
视觉方案通过在机器人上安装相机实现,利用照片之间隐藏的几何关系,解算出每张照片被拍摄时的相机位置、旋转等参数。
在计算机视觉中,这些参数的计算过程被称为“相机自动标定”,严格来说,是在微软研究院的[Zhang, 2000]中被称为“相机标定”(Camera Calibration),并且介绍了单应矩阵估算、相机内部参数矩阵估算、相机外部参数矩阵估算。内部参数矩阵包括相机的焦距、传感器尺寸等,而外部参数矩阵就是相机自身的位移和旋转。计算背后的几何基础是投影理论、对极几何,物理基础是相机镜头成像原理。计算时,需要使用两张照片,第一张作为参考,计算得到的位移是以拍摄第一张照片的相机位置为参考的;计算得到的旋转,也是以第一张照片为参考的。
[Zhang, 2000]的计算思路是利用单应矩阵对相机内参矩阵进行估算,进而得到相机的位置和姿态。因此,我们拍摄5张照片,以第一张照片为基础,分别用后四张照片与第一张配对,寻找匹配点,并按照上述计算方法得到相机的内部参数(包括焦距、传感器尺寸等)和外部参数(相机相对坐标和旋转)。
在[Zhang, 2000]的算法中,对位置的解算存在缺陷,我们在后文中,继续参考美国宾夕法尼亚大学的机器人教程,进行位置解算。大致的解算流程如下,首先根据匹配点估算基本矩阵(Fundamental Matrix),再使用基本矩阵和相机内参矩阵估算本质矩阵(Essential Matrix),最后利用本质矩阵估算相机位移、相机旋转和匹配点三维坐标。
一 单应矩阵(Homography)的估算-微软研究院
1 SIFT
SIFT是一种数学算法,用来寻找两张照片中的相同点(称为匹配点)。本实验中,由于图片像素尺寸较大,而实验地点在深圳一家星巴克,为了节省计算时间,对图片做了降采样处理,在像素坐标上,变成了原本的0.2倍。
2 单应矩阵
单应矩阵构建了点在两张照片中的像素坐标转换关系,用数学表达的话,令x表示点在照片1中的坐标,x’表示这个点在照片2中的坐标,且令照片1为参考照片。单应矩阵,以H表示,为3*3的矩阵,一共九个元素,作为未知数,至少需要9个方程才能够求解(注意:H的自由度实际上是8,由于还存在一个用于矩阵整体缩放的参数,一共9个,在这里不作介绍)。由于每一组匹配点能够提供两个方程,因此,至少需要5组匹配点,制造出10个方程,才能够求解9个未知数。在至少5个匹配点的情况下,方程组的数量超过未知数的个数,在线性代数中称为超定方程,是不一定有解的,这是因为数据来自于实际测量,存在误差引入,导致每一个方程都出现偏差。对于这种情况,我们不用得到精确解(实际上不存在),只需要得到一个最贴近所有方程的解即可,为了达到这个目标一般使用估算的方法,比如最小二乘法、极大似然估计法。

图1 单应矩阵计算方程
3 开发案例1——相机自动标定开发第三阶段第一次开发
在深圳福田的星巴克内,拍摄了五张照片,以第一张为基准,用后四张分别与其进行配对,通过匹配点估算单应矩阵。
使用期望、绝对误差和方差进行评价,认为H*x1的结果是估算值,x2是真实值。但是,每一个点的坐标都是不同的,如果针对每一个点分析的话,每一个点只有一次估计,无法进行统计。相对的,H*x1与x2的距离是一个不错的参数,一次单应矩阵的估算中,每一个x2点,其估算结果与x2真值的距离,在理论上应该是0,也就是真值的期望是0。因此,针对距离进行评价,一组照片中的所有点都是样本。
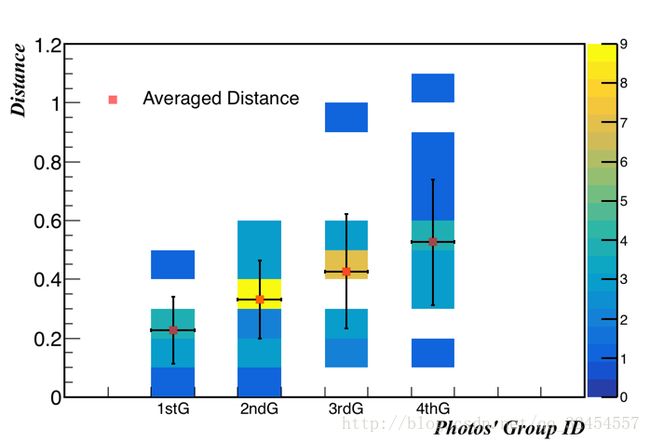
设定一个点的计算值与真值的距离为d,一组照片中所有点的距离均值为d_ave,样本方差为sigma2,标准差为sigma。评价方式一:距离,作距离的二维直方图,照片组号(ID)为横坐标,距离为纵坐标;评价方式二:距离均值,作距离的一维直方图,照片组号(ID)为横坐标,距离均值为横坐标的权重,样本标准差为误差。
可以看到离散程度在逐渐增大(标准差在逐渐增大),这跟每一组的相机拍摄距离增大是一致的,可能相关。
二 相机内部参数矩阵(Cameral Intrinsic Matrix)的估算-微软研究院
1 IAC的估算
IAC是一个中间参数,称为The Image of the Absolute Conic,它连接了相机内部参数矩阵与单应矩阵,所以为了求取内参矩阵,可以先取得IAC,而IAC可以用单应矩阵得到。
单应矩阵与IAC的关系是:每一个单应矩阵可以制造两个有关IAC的方程,具体可参考[Zhang, 2000],他将IAC用B表示。需要注意,在[Zhang, 2000]的行文中,单应矩阵元素的角标是列在前、行在后的,与我们大学本科学习线性代数时的矩阵角标标注方式相反,我在相机标定的第二阶段开发时,就错在这个地方。具体计算过程见图2。

图2 IAC计算方程
2 相机内部参数矩阵的估算
在得到IAC矩阵之后,内参矩阵的所有元素均可以求解,[Zhang, 2000]中列出了各个元素的计算方程。
3 开发案例1——相机自动标定开发第三阶段第一次开发
在星巴克拍摄了五张照片,拍摄了五张照片,以第一张为基准,用后四张分别与其进行配对,通过匹配点估算单应矩阵。
(1)IAC的评价
IAC以B表示,与每一个单应矩阵独立地建立数学关系,并且提供两个方程,参见[Zhang, 2000]。为方便表述,这里简要列举,以H表示单应矩阵,且H=(h1, h2, h3),有h1T*B*h2=0,h1T*B*h1-h2T*B*h2=0。IAC的估算需要所有组的照片一起进行,所以对IAC的误差分析需要考虑所有照片组。
在我们这里,一共四组照片,可以提供8个方程。评价指标方面,与单应矩阵的评价不同,这里没有距离,但h1T*B*h2,h1T*B*h1-h2T*B*h2的结果也是单值的,可以作为评价指标使用,我们就如此进行。
分析结果如下图,虽然两个评价量的期望都是零,但是样本太少,不能确定此处的误差到底有多大,对后续的相机内参矩阵的估算的误差引入也不知道如何估计。
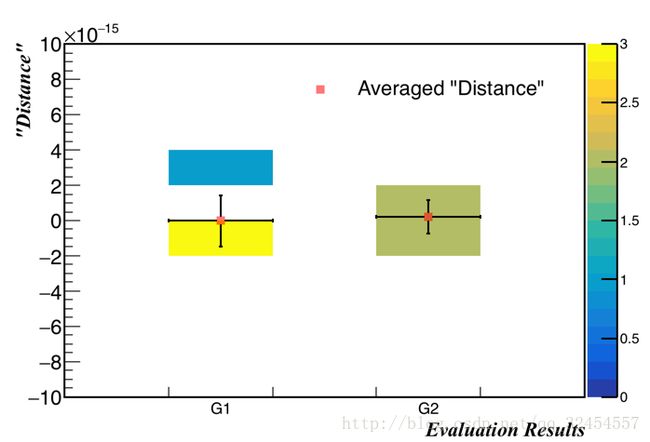
IAC评价图,G1是h1T*B*h2的绝对误差分析,G2是h1T*B*h1-h2T*B*h2的绝对误差分析
(2) 内参矩阵的评价
本次开发的内参矩阵参数如下:
alpha = 1156.76005135
beta = 1206.58063129
u0 = 33.0238094882
v0 = 385.638390652
lambda = 0.120263338283
gamma = 86.0313073062
相片的像素尺寸是3840 × 2160,理论上,u0=1920,v0=1080。估算与理论相比,属于量级差距,是非常大的差距。可以确定,SLAM解算流程的问题,出现在这里。
根据微软研究院的[Zhang, 2000],对本次开发进行重新分析,发现问题出现在单应矩阵的求解上。单应矩阵由两张照片计算得到,一张照片作为参照,一张照片作为对象。在[Zhang, 2000]的定位下,作为“参照”的照片,实际上是作为三维坐标点的承载物,因为[Zhang, 2000]强调了使用同一平面内的匹配点,同时将这个平面摆放在了特殊的角度,使所有匹配点在Z分量上均为0,因而在单应矩阵的计算中,本该提供三维信息的匹配点,仅需要提供二维信息即可,也就是提供匹配点的“照片”,也就是所谓的“参考”照片。
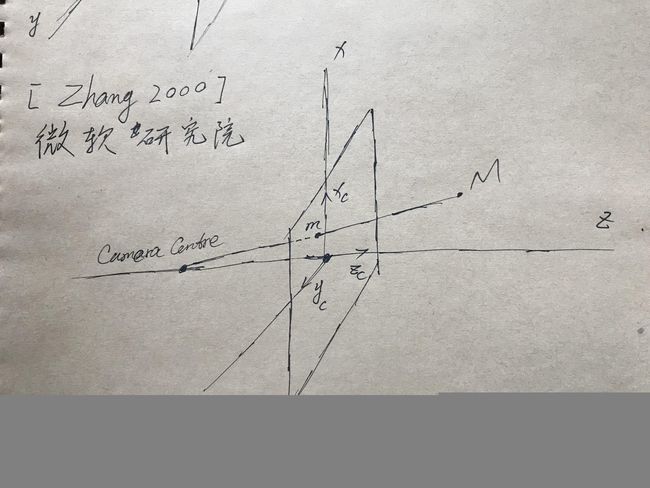
全局坐标系(global coordinate system)和相机坐标系(first camera coordinate system)
[Zhang, 2000]如此巧妙构造的前提是,所有匹配点均分布在同一平面内,且垂直于全局坐标系的Z轴,而且相机坐标系与全局坐标系的三个分量朝向一致,相机的成像平面垂直于全局坐标系的Z轴,且在Z=0处。
回到本阶段开发的讨论,我提供的“参考”照片并不符合[Zhang, 2000]的需求,见下图。

(a) 我提供的“参考”照片,不符合[Zhang, 2000]需要,(b) “参照”照片,符合[Zhang, 2000]需要
(3) 错误原因分析
物理框架层面上,是“参考”照片选择有误。
程序实现层面,有几个问题,首先是图片坐标,为了加快SIFT处理速度,图片在Matlab下首先使用将采样的方法,将坐标缩小为原来的0.2倍,所以在开始解算前,需要将坐标还原。我发生的问题是将0.2倍认为是面积缩小为0.2倍,实际上是一维上缩小为0.2倍。
第二个问题是SIFT结果,以匹配点坐标数据的形式导出,一行四个数,前两个为“参考”照片中的像素坐标,按照x、y的顺序给出,后两个是待解算照片中的匹配点坐标,同样以x、y的顺序给出。但是,这个匹配点坐标的x分量,是被加上了1200的,因为在Matlab中,两张图片为左右放置,待解算图片位于右边,两张照片倍合成为了一张,匹配点的坐标均在这个坐标系下。之所以是加上了1200,是因为原本照片的x方向长度为6000像素,是我的Sony微单的分辨率,但由于做了降采样,缩放比例为0.2,导致x方向的长度缩减为1200像素。所以在处理之前,需要将待解算图片的匹配点的x坐标减去1200。
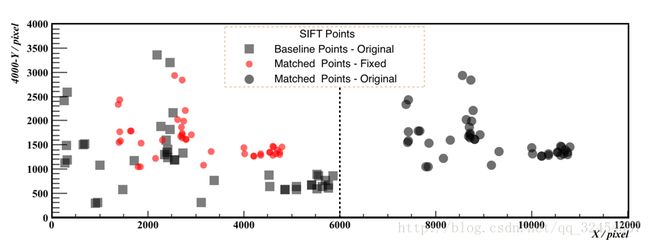
匹配点原始数据和处理结果,Original为原始数据,Fixed为处理后的数据,Baseline是匹配点在“参考”照片中的坐标,Matched是匹配点在待解算照片中的坐标
第三个问题是在做相机内参矩阵解算的最后一步时,u0的计算方程中,本该是lambda的地方,被我错误地写上了gamma。另外,zhang的两篇论文中,有一篇对于u0的计算方程,写错了,本该鞋beta的地方,写上了alpha,需要注意。
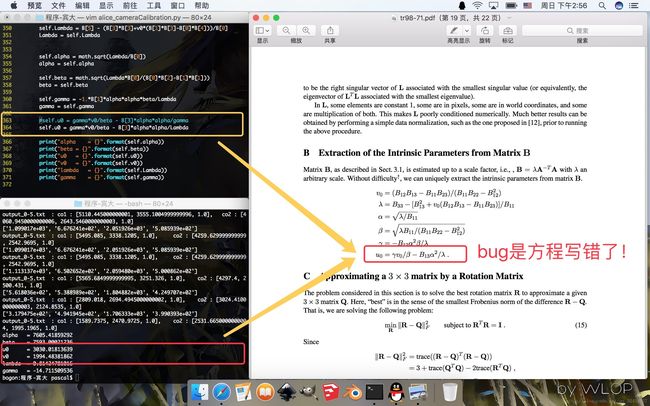
4 开发案例2——相机自动标定开发第三阶段第二次开发
在位于哈尔滨的住处拍摄了五张照片,照片中包含了以电脑显示的标定图片,分辨率为6000*4000,制作了相同分辨率的标定图片。
解算结果如下:
alpha = 7605
beta = 7593
u0 = 3030
v0 = 1994
lambda = 0.8142
gamma = -14.71
u0和v0为照片中心(principle center),理论上是照片中心的像素坐标(3000, 2000)。u0的绝对误差是30(pixel),相对误差是1%;v0的绝对误差是-6(pixel),相对误差是0.3%,认为匹配。
alpha和beta与相机传感器尺寸、像素以及镜头焦距有关,此次尝试使用Sony alpha 5100相机,传感器APS画幅,尺寸为23.5mm*15.6mm,像素尺寸为6000*4000,镜头为腾龙(Tamron) 18-200 mm,此次拍摄的焦距均为29.6mm。根据[Hartley R, 2000],alpha为f*mx,f为焦距,29.6mm,mx为传感器x方向上,单位长度的像素数量,为6000/23.5mm;因此,alpha=7557(pixel)。与alpha相同,beta是y方向上的因子,为7590(pixel)。alpha的绝对误差是48(pixel),相对误差是0.6%;beta的绝对误差是3(pixel),相对误差是0.04%,认为匹配。
| 参数名称 | 解算值 | 理论值 | 绝对误差 | 相对误差 |
|---|---|---|---|---|
| u0 / pixel | 3030 | 3000 | 30 | 1% |
| v0 / pixel | 1994 | 2000 | -6 | 0.3% |
| alpha / pixel | 7605 | 7557 | 48 | 0.6% |
| beta / pixel | 7593 | 7590 | 3 | 0.04% |
三 相机外部参数矩阵(Cameral External Matrix)的估算-微软研究院
相机外部参数矩阵由相机自身的平移和旋转构成,可以由相机内参矩阵和单应矩阵求解得到。其中的算法重点是内参矩阵的逆矩阵求解。
逆矩阵的求解方法有多种,如初等变换法、伴随阵法等等,由于求解对象是内参矩阵,为3*3的上三角矩阵,且使用程序解算,使用伴随阵法比较合适。
相机坐标解算结果见图,其中还是有缺陷,接下来参考宾夕法尼亚大学的计算机视觉教程继续调试。

图3 内参矩阵求逆
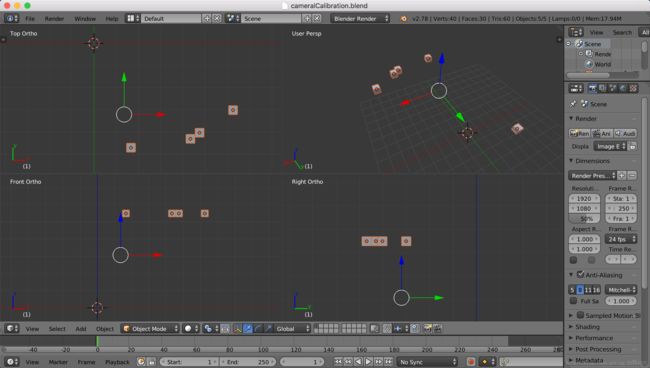
图4 相机位置计算结果(blender显示)
四 基本矩阵(Fundamental Matrix)估算、筛选、整理和评价-宾大
1 基本矩阵的估算-最小二乘法
基本矩阵(Fundamental Matrix)构建了匹配点x1, x2的函数关系,以3*3矩阵的形式表达。基本矩阵F的矩阵方程为x2T*F*x1=0,使用匹配点构建矩阵,采用最小二乘法,对F的元素进行估算。
2 基本矩阵的筛选-RANSAC
由于存在错误匹配的情况,如果在最小二乘法中考虑了这些匹配点,将会使估算得到的基本矩阵严重偏离真实解。在这种情况下,需要对匹配点进行筛选,剔除错误匹配点。在宾大的视频教程中,推荐使用RANSAC算法进行筛选。
以x2T*F*x1的数值作为评价,也就是RANSAC中所说的“距离”。理论上,使用无误差的基本矩阵和正确且无误差的匹配点x1和x2,计算结果是0。而使用有误差的匹配点,和有误差的基本矩阵,计算结果将偏离0。我们这里,以计算结果的绝对值为评价,或者说“距离”,带入RANSAC算法中。
之所以能这么做,是默认了发生错误匹配的情况占少数,那么统计上,错误匹配点的数量只占少数。
五 本质矩阵(Essential Matrix)估算-宾大
宾大的相机外部参数解算以基本矩阵F和相机内部参数矩阵K为基础。
首先估算基本矩阵,并对基本矩阵进行整理(Cleanup),然后估算本质矩阵E,E = KT*F*K。
六 相机位置和姿态估算-宾大
附录1——矩阵的奇异分解(SVD)
参考(http://www.cnblogs.com/whu-zeng/p/4705970.html ),A=UDVT,ATA的特征向量构成V,AAT的特征向量构成U。
[Hartley R, 2000] Hartley R, Zisserman A. Multiple view geometry in computer vision[C]// Cambridge University Press, 2000:1865 - 1872.
[Zhang, 2000] Zhang Z. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(11):1330-1334.