Paper Notes: A Comprehensive Survey on Graph Neural Networks

A Comprehensive Survey on Graph Neural Networks

• LINK: https://arxiv.org/abs/1901.00596

• CLASSIFICATION: GNN, SURVEY

• YEAR: Submitted on 3 Jan 2019 (v1), last revised 4 Dec 2019 (this version, v4)

• FROM: ArXiv 2019

• WHAT PROBLEM TO SOLVE: Existing surveys only include some of the GNNs and examine a limited number of works, thereby missing the most recent development of GNNs.

• SOLUTION:

  This paper makes notable contributions summarized as follows:

  • New taxonomy

    Recurrent graph neural networks, Convolutional graph neural networks, Graph autoencoders, and Spatial-temporal graph neural networks.

  • Comprehensive review

    Provide detailed descriptions on representative models, make the necessary comparison, and summarise the corresponding algorithms.

  • Abundant resources

    Including state-of-the-art models, benchmark data sets, open-source codes, and practical applications.

  • Future directions

    Model depth, scalability trade-off, heterogeneity, and dynamicity.

• CORE POINT:

  • Taxonomy of GNNs

    • RecGNNs: Aim to learn node representations with recurrent neural architectures. They assume a node in a graph constantly exchanges information/message with its neighbors until a stable equilibrium is reached.

    • ConvGNNs: Generate a node v’s representation by aggregating its own features xv and neighbors’ features xu, where u ∈ N(v). Different from RecGNNs, ConvGNNs stack multiple graph convolutional layers to extract high-level node representations.

      

      

    • GAEs: Unsupervised learning frameworks which encode nodes/graphs into a latent vector space and reconstruct graph data from the encoded information. GAEs are used to learn network embeddings and graph generative distributions.

      

    • STGNNs: Consider spatial dependency and temporal dependency at the same time. Many current approaches integrate graph convolutions to capture spatial dependency with RNNs or CNNs to model the temporal dependency.

      

  • Level Tasks

    • Node-level: Outputs relate to node regression and node classification tasks with a multi-perceptron or a softmax layer as the output layer. RecGNNs and ConvGNNs can extract high-level node representations by information propagation/graph convolution.
    • Edge-level: With two nodes’ hidden representations from GNNs as inputs, a similarity function or a neural network can be utilized to predict the label/connection strength of an edge.
    • Graph-level: Outputs relate to the graph classification task. To obtain a compact representation on the graph level, GNNs are often combined with pooling and readout operations.

  • Training Framework

    • Semi-supervised learning for node-level classification: Given a single network with partial nodes being labeled and others remaining unlabeled, ConvGNNs can learn a robust model that effectively identifies the class labels for the unlabeled nodes.
    • Supervised learning for graph-level classification: Graph-level classification aims to predict the class label(s) for an entire graph. The end-to-end learning for this task can be realized with a combination of graph convolutional layers, graph pooling layers, and/or readout layers.
    • Unsupervised learning for graph embedding: When no class labels are available in graphs, we can learn the graph embedding in a purely unsupervised way in an end-to-end framework.

  • Representative RecGNNs and ConvGNNs

    O(m) if the graph adjacency matrix is sparse and is O(n^2) otherwise, O(n^3) due to some other operations.

  • RECURRENT GRAPH NEURAL NETWORKS

    Apply the same set of parameters recurrently over nodes in a graph to extract high-level node representations.

    

    • Graph Neural Network (GNN*)
    • Graph Echo State Network (GraphESN)
    • Gated Graph Neural Network (GGNN)
    • Stochastic Steady-state Embedding (SSE)

  • CONVOLUTIONAL GRAPH NEURAL NETWORKS

    Instead of iterating node states with contractive constraints, ConvGNNs address the cyclic mutual dependencies architecturally using a fixed number of layers with different weights in each layer.

    

    1. Spectral-based ConvGNNs

       Graph convolution of the input signal x with a filter g ∈ $R_n$ is defined as:

       

       If we denote a filter as $g\theta =diag(U_g^T)$, then the spectral graph convolution is simplified as:

       

       Spectral-based ConvGNNs all follow this definition. The key difference lies in the choice of the filter $g_{\theta }$.

       • Spectral Convolutional Neural Network (Spectral CNN)
       • Chebyshev Spectral CNN (ChebNet)
       • CayleyNet
       • Graph Convolutional Network (GCN)
       • Adaptive Graph Convolutional Network (AGCN)
       • Dual Graph Convolutional Network (DGCN)

    2. Spatial-based ConvGNNs

    The spatial-based graph convolutions convolve the central node’s representation with its neighbors’ representations to derive the updated representation for the central node. From another perspective, spatial-based ConvGNNs share the same idea of information propagation/message passing with RecGNNs. The spatial graph convolutional operation essentially propagates node information along edges.

    • Neural Network for Graphs (NN4G)

    • Contextual Graph Markov Model (CGMM)

    • Diffusion Convolutional Neural Network (DCNN)

    • Diffusion Graph Convolution (DGC)

    • PGC-DGCNN

    • Partition Graph Convolution (PGC)

    • Message Passing Neural Network (MPNN): Outlines a general framework of spatial-based ConvGNNs. It treats graph convolutions as a message passing process in which information can be passed from one node to another along edges directly. MPNN runs K-step message passing iterations to let information propagate further. The message passing function (namely the spatial graph convolution) is defined as:

      

      MPNN can cover many existing GNNs by assuming different forms of $U_k(\cdot ),M_k(\cdot ),andR(\cdot )$.

    • Graph Isomorphism Network (GIN)

    • GraphSage

    • Graph Attention Network (GAT)

      

    • Gated Attention Network (GAAN)

    • GeniePath

    • Mixture Model Network (MoNet)

    • PATCHY-SAN

    • Large-scale Graph Convolutional Network (LGCN)

    • Improvement in terms of training efficiency

      Training ConvGNNs such as GCN [22] usually is required to save the whole graph data and intermediate states of all nodes into memory. The full-batch training algorithm for ConvGNNs suffers significantly from the memory overflow problem, especially when a graph contains millions of nodes.

      

    • Comparison between spectral and spatial models

      spatial models are preferred over spectral models due to efficiency, generality, and flexibility issues.

      1. Spectral models are less efficient than spatial models.
      2. Spectral models which rely on a graph Fourier basis generalize poorly to new graphs.
      3. Spectral-based models are limited to operate on undirected graphs.

    3. Graph Pooling Modules

       • Graclus algorithm
       • mean/max/sum pooling
       • SortPooling
       • DiffPool
       • SAGPool

    4. Discussion of Theoretical Aspects

       • Shape of receptive field

         As a result, a ConvGNN is able to extract global information by stacking local graph convolutional layers.

       • VC dimension

       • Graph isomorphism

         common GNNs such as GCN and GraphSage are incapable of distinguishing different graph structures. If the aggregation functions and the readout functions of a GNN are injective, the GNN is at most as powerful as the WL test in distinguishing different graphs.

       • Equivariance and invariance

         A GNN must be an equivariant function when performing node-level tasks and must be an invariant function when performing graph-level tasks.

       • Universal approximation

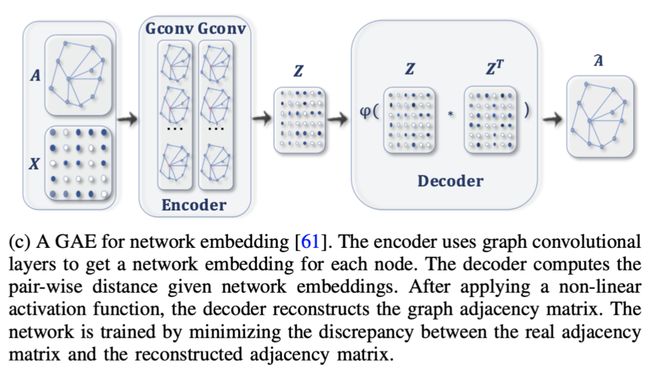
  • GRAPH AUTOENCODERS

    Graph autoencoders (GAEs) are deep neural architectures which map nodes into a latent feature space and decode graph information from latent representations.

    1. Network Embedding

       GAEs learn network embeddings using an encoder to extract network embeddings and using a decoder to enforce network embeddings to preserve the graph topological information such as the PPMI matrix and the adjacency matrix.

       • Deep Neural Network for Graph Representations (DNGR)
       • Structural Deep Network Embedding (SDNE)
       • Graph Autoencoder (GAE*)
       • Variational Graph Autoencoder (VGAE)
       • Adversarially Regularized Variational Graph Autoencoder (ARVGA)
       • Deep Recursive Network Embedding (DRNE)
       • Network Representations with Adversarially Regularized Autoencoders (NetRA)

    2. Graph Generation

       With multiple graphs, GAEs are able to learn the generative distribution of graphs by encoding graphs into hidden representations and decoding a graph structure given hidden representations.

       • Deep Generative Model of Graphs (DeepGMG)
       • GraphRNN
       • Graph Variational Autoencoder (GraphVAE)
       • Regularized Graph Variational Autoencoder (RGVAE)
       • Molecular Generative Adversarial Network (MolGAN)
       • NetGAN

       In brief, sequential approaches linearize graphs into sequences. They can lose structural information due to the presence of cycles. Global approaches produce a graph all at once. They are not scalable to large graphs as the output space of a GAE is up to $O(n^2)$.

  • SPATIAL-TEMPORAL GRAPH NEURAL NETWORKS

    STGNNs capture spatial and temporal dependencies of a graph simultaneously. The task of STGNNs can be forecasting future node values or labels, or predicting spatial-temporal graph labels. STGNNs follow two directions, RNN-based methods and CNN-based methods.

    1. RNN-based

       Most RNN-based approaches capture spatial-temporal dependencies by filtering inputs and hidden states passed to a recurrent unit using graph convolutions.

       RNN-based approaches suffer from time-consuming iterative propagation and gradient explosion/vanishing issues.

       • Graph Convolutional Recurrent Network (GCRN)
       • Diffusion Convolutional Recurrent Neural Network (DCRNN)

    2. CNN-based

       CNN-based approaches tackle spatial-temporal graphs in a non-recursive manner with the advantages of parallel computing, stable gradients, and low memory requirements.

       CNN-based approaches interleave 1D-CNN layers with graph convolutional layers to learn temporal and spatial dependencies respectively.

       • CGCN
       • ST-GCN
       • Graph WaveNet
       • GaAN
       • ASTGCN

  • APPLICATIONS

    1. Data Sets

       

    2. Evaluation & Open-source Implementations

       

       • Node Classification: In node classification, most methods follow a standard split of train/valid/test on benchmark data sets including Cora, Citeseer, Pubmed, PPI, and Reddit. They reported the average accuracy or F1 score on the test data set over multiple runs.

       • Graph Classification: A double cv method, which uses an external k fold cv for model assessment and an inner k fold cv for model selection.

       • Open-source implementations

         • A geometric learning library in PyTorch named PyTorch Geometric, which implements many GNNs
         • The Deep Graph Library (DGL) is released which provides a fast implementation of many GNNs on top of popular deep learning platforms such as PyTorch and MXNet

    3. Practical Applications

       • Computer vision

         Applications of GNNs in computer vision include scene graph generation, point clouds classification, and action recognition.

       • Natural language processing

         A common application of GNNs in natural language processing is text classification.
         GNNs utilize the inter-relations of documents or words to infer document labels.

       • Traffic

         Forecasting traffic speed, volume or the density of roads in traffic networks.

         Another industrial-level application is taxi-demand prediction with historical taxi demands, location information, weather data, and event features.

       • Recommender systems

         Graph-based recommender systems take items and users as nodes. By leveraging the relations between items and items, users and users, users and items, as well as content information, graph-based recommender systems are able to produce high-quality recommendations. The key to a recommender system is to score the importance of an item to a user. As a result, it can be cast as a link prediction problem.

         • R. van den Berg, T. N. Kipf, and M. Welling, “Graph convolutional matrix completion,” stat, vol. 1050, p. 7, 2017.
         • R. Ying, R. He, K. Chen, P. Eksombatchai, W. L. Hamilton, and J. Leskovec, “Graph convolutional neural networks for web-scale recommender systems,” in Proc. of KDD.
           ACM, 2018, pp. 974–983.
         • F. Monti, M. Bronstein, and X. Bresson, “Geometric matrix completion with recurrent multi-graph neural networks,” in Proc. of NIPS, 2017, pp. 3697–3707.

       • Chemistry

         In the field of chemistry, researchers apply GNNs to study the graph structure of molecules/compounds.

       • Others

         Program verification, program reasoning, social influence prediction, adversarial attacks prevention, electrical health records modeling, brain networks, event detection, and combinatorial optimization.

  • FUTURE DIRECTIONS

    • Model depth

      The performance of a ConvGNN drops dramatically with an increase in the number of graph convolutional layers.

      In theory, with an infinite number of graph convolutional layers, all nodes’ representations will converge to a single point. This raises the question of whether going deep is still a good strategy for learning graph data.

    • Scallability trade-off

      The scalability of GNNs is gained at the price of corrupting graph completeness. Whether using sampling or clustering, a model will lose part of the graph information.

    • Heterogenity

      It is difficult to directly apply current GNNs to heterogeneous graphs, which may contain different types of nodes and edges, or different forms of node and edge inputs, such as images and text.

    • Dynamicity

      Graphs are in nature dynamic in a way that nodes or edges may appear or disappear, and that node/edge inputs may change time by time.

• EXISTING PROBLEMS: 404

• IMPROVEMENT IDEAS: 404

---