《视觉slam十四讲》第3讲课后习题

首先讲将课后习题做一遍是个温习本书内容的过程。

1.验证旋转矩阵是正交矩阵：

首先明白什么是旋转矩阵，根据树上p42页定义，旋转矩阵R：

其中，为原单位正交基，为旋转后的单位正交基。在这只要求验证（实矩阵）旋转矩阵是正交矩阵，即就可以了。

注意，这里的表示的是向量，不是标量。

如果从代数的角度进行纯粹的化简证明，那这个证明的工作量就会明显大很多，而且没有直观上上的意义。数学本来的意义就在于能够让人更简单更直观描述一些客观事物的存在或是运动。

 所以我们可以换一种方式进行证明。根据矩阵的几何意义，旋转矩阵的逆表示为从旋转后单位正交基到原单位正交基的变换。即在书中p41页等式3.4构造，对等式两边同乘以，可得：

其中上标T代表着单位正交基转置的意思，不影响向量之间点积的值，不难发现对于旋转矩阵而言，从而，故旋转矩阵为正交矩阵。实际上正交矩阵的一大特点是矩阵行列式为，旋转矩阵的行列式为1,行列式为-1的矩阵有兴趣的可以去了解一下，一般称为镜像矩阵。

 

2.寻找罗德里格斯公式的推导过程并加以理解

1个旋转矩阵大多数情况下可以由3个欧拉角表示（为什么说大多数情况，因为欧拉角存在万向锁问题），但是一个3X3的旋转矩阵拥有9个元素，这显得旋转这种运动的表述有些累赘，所以应该有更好的表示方法，也就是罗德里格斯公式对其进行表示。罗德里格斯公式的目的是用一个旋转轴和一个旋转角描述一个旋转运动。在欧氏空间里，旋转轴（空间直线）可以由3个参数表示，旋转角仅需要1个参数就可以了。那么旋转矩阵和罗德里格斯公式之间的转换关系是怎么样的呢？

网上基本都是从wiki上从做图算向量角度上对公式进行推导，在后面的章节中我们会学到SO(3)的李群映射，相交于做图而言，用映射进行推导会简洁许多。根据李代数定义：( 或者 )，每个旋转矩阵都会对应一个三维向量，三维向量又可以将其方向和模长分开表示，即。

对于旋转矩阵：

得证。

对于上式推导需要一点李群里代数基础，不懂的可以再看看书。

 

3. 验证四元数旋转某个点后，结果是个虚四元数，所以仍然对应到一个三维空间点

三维点，经过一个旋转，所以新得到的点设为。根据四元素乘法运算性质，先计算前半部分：

对于后半段，

对于虚四元数，我们只需要验证结果的实数部分是0就可以了，其实数部分s：

进行展开消元化简得：

s=0，因此，结果仍旧是个虚四元数，仍旧是个3D坐标。

 

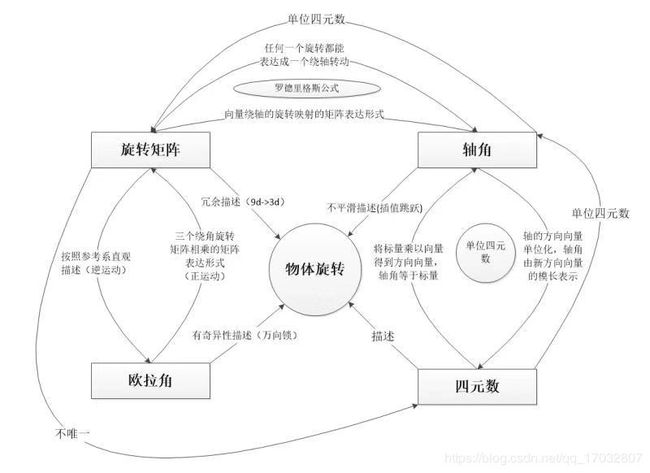
4.画表总结旋转矩阵、轴角、欧拉角、四元数的关系

 

5.假设有一个大的Eigen矩阵，想把它左上角3X3的块取出来，然后赋值为，请编程实现。

直接双重for循环遍历前3行3列，进行矩阵元素赋值操作。

 

6.一般线性方程有几种解法？

一般分为直接法和雅克比迭代法。直接法分为：1.直接求逆法，运算量大，仅对方阵有效，很可能没解；2.QR分解法，一般比较常用，方程就算方程无解也会得到近似解；3.最小二乘求解，和QR类似；4.LU分解法，仅仅对于方阵有效；5.cholesky分解法，也仅仅适合方阵。雅克比迭代法属于一种数值求解法，需要计算方程的雅克比矩阵以及设计迭代策略。

 

7.设有小萝卜一号和小萝卜二号位于世界坐标系中。小萝卜一号的位姿为，,这里和表达的是，也就是世界坐标系到相机坐标系的变换关系。小萝卜二号位姿为，。现在小萝卜一号看到一个点在自身坐标系下坐标为，求该点在小萝卜二号坐标系下的坐标。请编程实现。

分析：

目前在编程中，涉及到坐标系变换一般是利用位姿变化矩阵进行实现。所以首先应当将其转化为位姿变化矩阵。由于在世界坐标系下，被观测点属于静态不动点，所以被观测点的世界坐标系下坐标为常量，由此构建被观测点在两个小萝卜坐标系的投影坐标的恒等式。假设该点在小萝卜二号坐标系下的坐标为，小萝卜一号位姿矩阵为，小萝卜二号的位姿矩阵为，则可列等式：

由此可进行编程求解坐标：

CMakeLists.txt如下所示：

cmake_minimum_required(VERSION 2.6)
project(homeworks3_7)

include_directories("/usr/include/eigen3")

add_executable(homeworks3_7 main.cpp)

install(TARGETS homeworks3_7 RUNTIME DESTINATION bin)

main.cpp如下所示：

#include 
#include 
#include 

using namespace std;


int main(int argc, char **argv) {
  
  //导入小萝卜一号数据  
  Eigen::Quaterniond q1 (0.35, 0.2, 0.3, 0.1);
  Eigen::Vector3d t1 (0.3, 0.1, 0.1);
  //导入小萝卜二号数据
  Eigen::Quaterniond q2 (-0.5, 0.4, -0.1, 0.2);
  Eigen::Vector3d t2 (-0.1, 0.5, 0.3);
  //导入小萝卜一号观测观测点数据
  Eigen::Vector3d p (0.5, 0, 0.2);
  //定义小萝卜二号观测观测点坐标
  Eigen::Vector3d o;
  
  //初始化欧式变换矩阵
  Eigen::Isometry3d T_1cw = Eigen::Isometry3d::Identity();
  Eigen::Isometry3d T_2cw = Eigen::Isometry3d::Identity();
  
  //开始求解
  //归一化四元数
  q1.normalize();
  q2.normalize();
  //输出归一化后信息
  cout<<"q1 = "<< endl << q1.x()<在KDevelop输出结果如图所示：