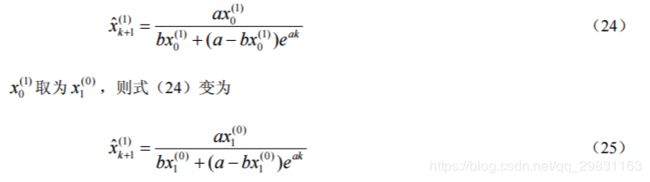灰色系统理论及其应用 (七) ：道路交通事故灰色 Verhulst 预测模型

---

灰色系统理论及其应用系列博文：

灰色系统理论及其应用 (一) ：灰色系统概论、关联分析、与传统统计方法的比较

灰色系统理论及其应用 (二) ：优势分析

灰色系统理论及其应用 (三) ：生成数

灰色系统理论及其应用 (四) ：灰色模型 GM

灰色系统理论及其应用 (五) ：灰色预测

灰色系统理论及其应用 (六) ：SARS 疫情对某些经济指标影响问题

灰色系统理论及其应用 (七) ：道路交通事故灰色 Verhulst 预测模型

灰色系统理论及其应用 (八) ：GM(2,1)和 DGM 模型

灰色系统理论及其应用 (九) ： GM(1, N) 和GM(0, N) 模型

---

目录

1 Verhulst 模型简介                                              参数列的最小二乘估计

2 道路交通事故 Verhulst 预测模型                        3 预测结果比较                              4 结语

---

灰色预测是通过原始数据的处理和灰色模型的建立，发现和掌握系统发展规律，对 系统的未来状态作出科学的定量预测。目前应用较多的灰色预测模型是 GM(1,1)模型、 灰色马尔可夫预测模型等，可用于预测交通事故发生次数、死亡人数、受伤人数和财产 损失等指标。GM(1,1)模型适用于具有较强指数规律的序列，只能描述单调的变化过程。但是道路交通系统是一个动态的时变系统，道路交通事故作为道路系统的行为特征量， 具有一定的随机波动性，它的发展呈现某种变化趋势的非平稳随机过程，因此可建立交 通事故灰色马尔可夫预测模型，以提高预测精度。但灰色马尔可夫预测模型的应用难点 是如何进行状态划分，故对于非单调的摆动发展序列或具有饱和状态的 S 形序列， Verhulst 模型，GM(2,1)模型等更适用。

Verhulst 模型主要用来描述具有饱和状态的过程， 即 S 形过程，常用于人口预测、生物生长、繁殖预测及产品经济寿命预测等。今年来 中国道路交通事故表现为具有饱和状态的 S 形过程，故可采用 Verhulst 模型对其进行预 测。

1 Verhulst 模型简介

Verhulst 模型的基本原理和计算方法简介图下

参数列的最小二乘估计

 定理 2       设灰色 Verhulst 模型如上所述，则白化方程的解（时间响应函数）为

灰色 Verhulst 模型的时间响应序列为

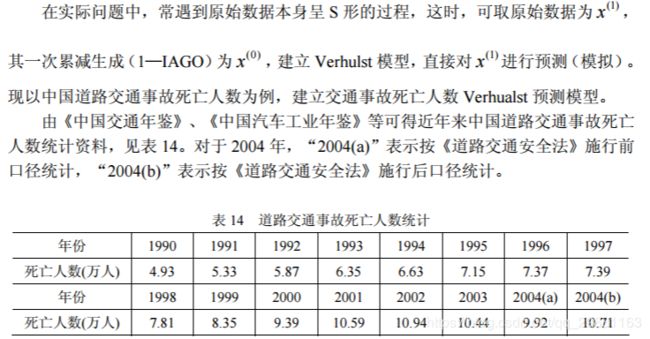
累减还原式为

2 道路交通事故 Verhulst 预测模型

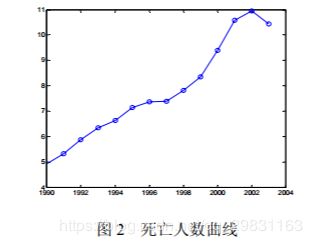
1990～2003 年中国道路交通事故死亡人数曲线见图 2，可见曲线呈 S 形，故可建立 Verhulst 模型进行预测，其建模过程如下。

（7）模型精度检验。

一个灰色模型要经过检验才能判定其是否合理。只有通过检 验的模型才能用来进行预测。检验方法有以下几种。

① 残差合格模型

② 关联度合格模型

 ③ 均方差比合格模型

④ 小误差概率合格模型

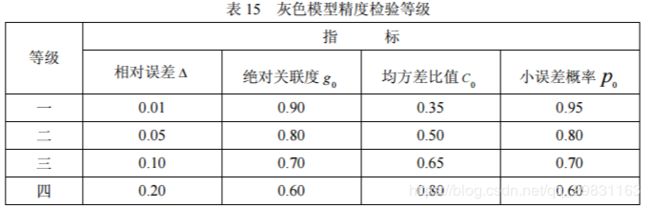
由上可知，给定一组取值，就确定了检验模型精度的一个等级。常用的精度等级见 表 15，可供检验模型参考。一般情况下，最常用的是相对误差检验指标。

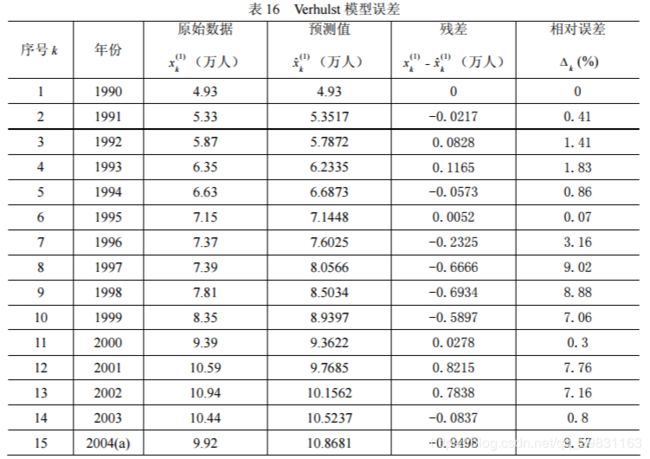
由以上检验方法，可得 1990～2003 年中国道路交通事故死亡人数 Verhulst 模型误 差检验值见表 16。

计算的 MATLAB 程序如下：

clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37 7.39 7.81 8.35
9.39 10.59 10.94 10.44];
n=length(x1);
nian=1990:2003;
plot(nian,x1,'o-');
x0=diff(x1);
x0=[x1(1),x0]
for i=2:n
    z1(i)=0.5*(x1(i)+x1(i-1));
end
z1
B=[-z1(2:end)',z1(2:end)'.^2]
Y=x0(2:end)'
abhat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b*x^2','x(0)=x0'); %求解常微分方程
x=subs(x,{'a','b','x0'},{abhat(1),abhat(2),x1(1)}); %代入参数值
yuce=subs(x,'t',0:14) %计算预测值
digits(6); x=vpa(x) %显示微分方程的解，为了提高计算精度，把该语句放在计算预测值之后，或者不使用该语句
yuce(16)=yuce(15);
x1_all=[x1,9.92,10.71];
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(1); %数据列的始点零化像
yuce_0=yuce-yuce(1); %数据列的始点零化像
s0=abs(sum(x1_all_0(1:end-1))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(1:end-1))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(1:end-1))+0.5*tt(end));
absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,1)/std(x1_all,1) %计算标准差比值

3 预测结果比较

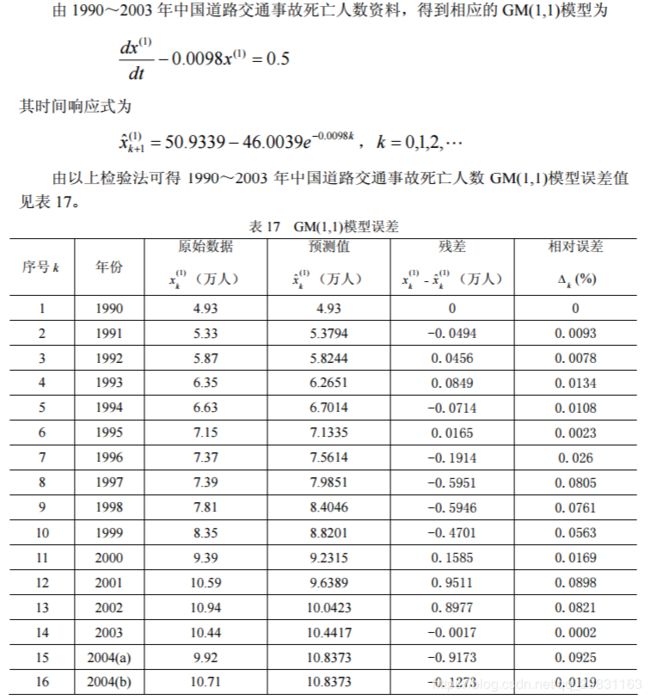
比较表 16 和表 17 可知，Verhulst 模型预测精度与 GM(1,1)模型几乎没有差别。 计算的 MATLAB 程序如下：

clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37 7.39 7.81 8.35
9.39 10.59 10.94 10.44]; 
n=length(x1);
x0=diff(x1);
x0=[x1(1),x0]
for i=2:n
    z1(i)=0.5*(x1(i)+x1(i-1));
end
B=[-z1(2:end)',ones(n-1,1)];
Y=x0(2:end)';
abhat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b','x(0)=x0');
x=subs(x,{'a','b','x0'},{abhat(1),abhat(2),x1(1)});
yuce=subs(x,'t',0:14) %计算预测值
digits(6); x=vpa(x) %显示微分方程的解，为了提高计算精度，把该语句放在计算预测
值之后，或者不使用该语句
yuce(16)=yuce(15);
x1_all=[x1,9.92,10.71];
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(1); %数据列的始点零化像
yuce_0=yuce-yuce(1); %数据列的始点零化像
s0=abs(sum(x1_all_0(1:end-1))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(1:end-1))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(1:end-1))+0.5*tt(end));
absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,1)/std(x1_all,1) %计算标准差比值

 4 结语

道路交通安全系统是一个灰色系统，可以应用灰色系统理论进行研究和分析，其中 灰色预测模型和方法简便易用，在交通事故预测中得到了较多应用。GM(1,1)模型适用 于具有较强指数规律的序列，只能描述单调的变化过程，而 Verhulst 模型则适用于非单 调的摆动发展序列或具有饱和状态的 S 形序列。

---

灰色系统理论及其应用系列博文：

灰色系统理论及其应用 (一) ：灰色系统概论、关联分析、与传统统计方法的比较

灰色系统理论及其应用 (二) ：优势分析

灰色系统理论及其应用 (三) ：生成数

灰色系统理论及其应用 (四) ：灰色模型 GM

灰色系统理论及其应用 (五) ：灰色预测

灰色系统理论及其应用 (六) ：SARS 疫情对某些经济指标影响问题

灰色系统理论及其应用 (七) ：道路交通事故灰色 Verhulst 预测模型

灰色系统理论及其应用 (八) ：GM(2,1)和 DGM 模型

灰色系统理论及其应用 (九) ： GM(1, N) 和GM(0, N) 模型

---