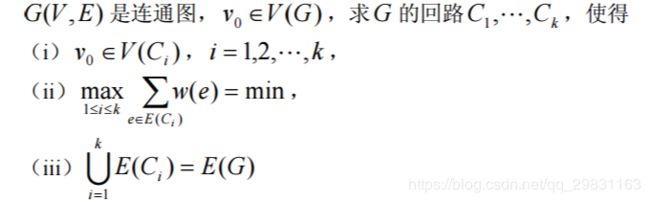Euler 图和 Hamilton 图 : 欧拉图 、哈密顿图

---

图&网络系列博文：

【1】图与网络模型及方法：图与网络的基本概念

【2】图&网络模型应用—最短路径问题

【3】树：基本概念与最小生成树

【4】匹配问题： 匈牙利算法 、最优指派、相等子图

【5】Euler 图和 Hamilton 图

【6】计划评审方法和关键路线法【统筹方法】：广泛地用于系统分析和项 目管理

【7】最小费用流及其求法 ：

【8】最大流问题  

【9】钢管订购和运输问题

---

目录

1 基本概念

2 Euler 回路的 Fleury 算法 

例 ：邮递员问题                    多邮递员问题

3 旅行商（TSP）问题 

3.1 改良圈算法                                  3.2  旅行商问题的数学表达式

---

1 基本概念

【定义】 经过G 的每条边的迹叫做G 的 Euler 迹；闭的 Euler 迹叫做 Euler 回路或 E 回路；含 Euler 回路的图叫做 Euler 图。 直观地讲，Euler 图就是从一顶点出发每边恰通过一次能回到出发点的那种图，即 不重复地行遍所有的边再回到出发点。

【定义 】包含G 的每个顶点的轨叫做 Hamilton(哈密顿)轨；闭的 Hamilton 轨叫做 Hamilton 圈或 H 圈；含 Hamilton 圈的图叫做 Hamilton 图。 直观地讲，Hamilton 图就是从一顶点出发每顶点恰通过一次能回到出发点的那种图，即不重复地行遍所有的顶点再回到出发点。

2 Euler 回路的 Fleury 算法

1921 年，Fleury 给出下面的求 Euler 回路的算法。 

例 ：邮递员问题

中国邮递员问题 一位邮递员从邮局选好邮件去投递，然后返回邮局，当然他必须经过他负责投递的 每条街道至少一次，为他设计一条投递路线，使得他行程最短。

上述中国邮递员问题的数学模型是：在一个赋权连通图上求一个含所有边的回路， 且使此回路的权最小。 显然，若此连通赋权图是 Euler 图，则可用 Fleury 算法求 Euler 回路，此回路即为 所求。

非 Euler 图的权最小的回路的求解方法

对于非 Euler 图，1973 年，Edmonds 和 Johnson 给出下面的解法：

多邮递员问题

 邮局有 k(k ≥ 2) 位投递员，同时投递信件，全城街道都要投递，完成任务返回邮 局，如何分配投递路线，使得完成投递任务的时间最早？我们把这一问题记成 kPP。 kPP 的数学模型如下：

3 旅行商（TSP）问题

一名推销员准备前往若干城市推销产品，然后回到他的出发地。如何为他设计一条 最短的旅行路线（从驻地出发，经过每个城市恰好一次，最后返回驻地）？这个问题称 为旅行商问题。用图论的术语说，就是在一个赋权完全图中，找出一个有最小权的 Hamilton 圈。称这种圈为最优圈。与最短路问题及连线问题相反，目前还没有求解旅行 商问题的有效算法。所以希望有一个方法以获得相当好（但不一定最优）的解。

3.1 改良圈算法

用改良圈算法得到的结果几乎可以肯定不是最优的。为了得到更高的精确度，可以 选择不同的初始圈，重复进行几次算法，以求得较精确的结果。 这个算法的优劣程度有时能用 Kruskal 算法加以说明。

假设C 是G 中的最优圈。 则对于任何顶点v ，C − v 是在G − v 中的 Hamilton 轨，因而也是G − v 的生成树。由 此推知：若 T 是 G − v 中的最优树，同时 e 和 f 是和 v 关联的两条边，并使得 w(e) + w( f ) 尽可能小，则 w(T ) + w(e) + w( f ) 将是 w(C) 的一个上界。 这里介绍的方法已被进一步发展。圈的修改过程一次替换三条边比一次仅替换两条 边更为有效；然而，有点奇怪的是，进一步推广这一想法，就不对了。

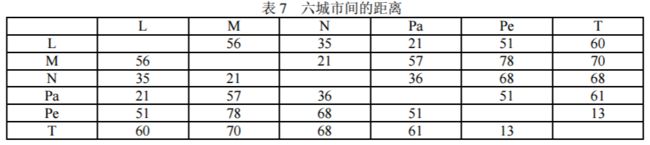
例 15 从北京（Pe）乘飞机到东京(T)、纽约(N)、墨西哥城(M)、伦敦(L)、巴黎(Pa) 五城市做旅游，每城市恰去一次再回北京，应如何安排旅游线，使旅程最短？各城市之 间的航线距离如表 7。

解：编写程序如下：

function main
clc,clear
global a
a=zeros(6);
a(1,2)=56;a(1,3)=35;a(1,4)=21;a(1,5)=51;a(1,6)=60;
a(2,3)=21;a(2,4)=57;a(2,5)=78;a(2,6)=70;
a(3,4)=36;a(3,5)=68;a(3,6)=68; a(4,5)=51;a(4,6)=61;
a(5,6)=13; a=a+a'; L=size(a,1);
c1=[5 1:4 6];
[circle,long]=modifycircle(c1,L);
c2=[5 6 1:4];%改变初始圈，该算法的最后一个顶点不动
[circle2,long2]=modifycircle(c2,L);
if long20
    flag=0;
    for m=1:L-3
        for n=m+2:L-1
            if a(c1(m),c1(n))+a(c1(m+1),c1(n+1))<...
                a(c1(m),c1(m+1))+a(c1(n),c1(n+1))
                flag=1;
                c1(m+1:n)=c1(n:-1:m+1);
            end
        end
    end
end
long=a(c1(1),c1(L));
for i=1:L-1
    long=long+a(c1(i),c1(i+1));
end
circle=c1; 

3.2  旅行商问题的数学表达式

将旅行商问题写成数学规划的具体形式还需要一定的技巧，下面的例子我们引用 LINGO 帮助中的一个程序。

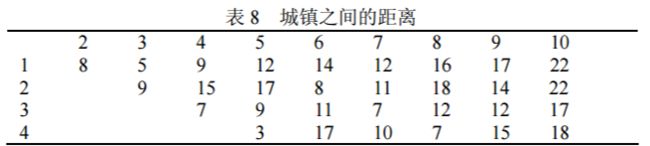
例 16  已知 SV 地区各城镇之间距离见表 8，某公司计划在 SV 地区做广告宣传， 推销员从城市 1 出发，经过各个城镇，再回到城市 1。为节约开支，公司希望推销员走 过这 10 个城镇的总距离最少。

解 编写 LINGO 程序如下：

MODEL:
 SETS:
 CITY / 1.. 10/: U; ! U( I) = sequence no. of city;
 LINK( CITY, CITY):
 DIST, ! The distance matrix;
 X; ! X( I, J) = 1 if we use link I, J;
 ENDSETS
 DATA: !Distance matrix, it need not be symmetric;
 DIST =0 8 5 9 12 14 12 16 17 22
 8 0 9 15 17 8 11 18 14 22
 5 9 0 7 9 11 7 12 12 17
 9 15 7 0 3 17 10 7 15 18
 12 17 9 3 0 8 10 6 15 15
 14 8 11 17 8 0 9 14 8 16
 12 11 7 10 10 9 0 8 6 11
 16 18 12 7 6 14 8 0 11 11
 17 14 12 15 15 8 6 11 0 10
 22 22 17 18 15 16 11 11 10 0;
 ENDDATA
 !The model:Ref. Desrochers & Laporte, OR Letters,
 Feb. 91;
 N = @SIZE( CITY);
 MIN = @SUM( LINK: DIST * X);
 @FOR( CITY( K):
 ! It must be entered;
 @SUM( CITY( I)| I #NE# K: X( I, K)) = 1;
 ! It must be departed;
 @SUM( CITY( J)| J #NE# K: X( K, J)) = 1;
 ! Weak form of the subtour breaking constraints;
 ! These are not very powerful for large problems;
 @FOR( CITY( J)| J #GT# 1 #AND# J #NE# K:
 U( J) >= U( K) + X ( K, J) -
 ( N - 2) * ( 1 - X( K, J)) +
 ( N - 3) * X( J, K)));
 ! Make the X's 0/1;
 @FOR( LINK: @BIN( X));
 ! For the first and last stop we know...;
 @FOR( CITY( K)| K #GT# 1:
 U( K) <= N - 1 - ( N - 2) * X( 1, K);
 U( K) >= 1 + ( N - 2) * X( K, 1));
END 

---

图&网络系列博文：

【1】图与网络模型及方法：图与网络的基本概念

【2】图&网络模型应用—最短路径问题

【3】树：基本概念与最小生成树

【4】匹配问题： 匈牙利算法 、最优指派、相等子图

【5】Euler 图和 Hamilton 图

【6】计划评审方法和关键路线法【统筹方法】：广泛地用于系统分析和项 目管理

【7】最小费用流及其求法 ：

【8】最大流问题  

【9】钢管订购和运输问题

---