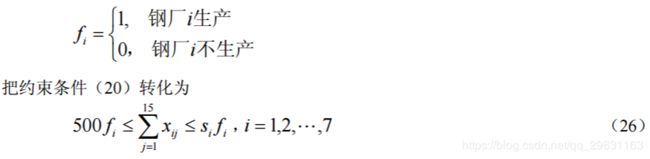钢管订购和运输

---

图与网络模型：

【1】图与网络模型及方法：图与网络的基本概念

【2】图&网络模型应用—最短路径问题

【3】树：基本概念与最小生成树

【4】匹配问题： 匈牙利算法 、最优指派、相等子图

【5】Euler 图和 Hamilton 图

【6】计划评审方法和关键路线法【统筹方法】：广泛地用于系统分析和项 目管理

【7】最小费用流及其求法 ：

【8】最大流问题  

【10】钢管订购和运输问题

---

目录

1 问题描述

2 模型的建立与求解

2.1 运费矩阵的计算模型

2.2 总费用的数学规划模型

2.3 Lingo代码

3 管道为树形图时的模型

---

1 问题描述

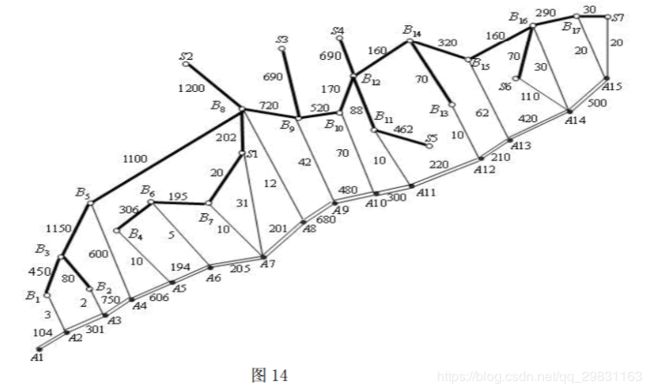
要铺设一条 A1 → A2 →.... → A15 的输送天然气的主管道, 如图 14 所示。经筛选后可以生产这种主管道钢管的钢厂有 S1 , S2,..., S7 。图中粗线表示铁路，单细线表示公 路，双细线表示要铺设的管道(假设沿管道或者原来有公路，或者建有施工公路)，圆圈 表示火车站，每段铁路、公路和管道旁的阿拉伯数字表示里程(单位 km)。

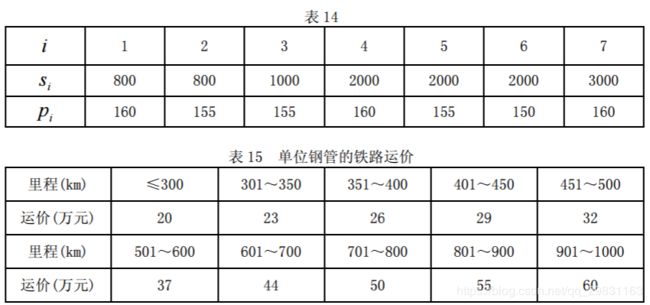
为方便计，1km 主管道钢管称为 1 单位钢管。 一个钢厂如果承担制造这种钢管，至少需要生产 500 个单位。钢厂 Si 在指定期限内能生产该钢管的最大数量为  si 个单位，钢管出厂销价 1 单位钢管为 pi 万元，见表 14； 1 单位钢管的铁路运价见表 15。

1000km 以上每增加 1 至 100km 运价增加 5 万元。公路运输费用为 1 单位钢管每公 里 0.1 万元（不足整公里部分按整公里计算）。钢管可由铁路、公路运往铺设地点（不 只是运到点  A1 , A 2,..., A 15，而是管道全线）。

（1）请制定一个主管道钢管的订购和运输计划，使总费用最小（给出总费用)。

（2）请就（1）的模型分析：哪个钢厂钢管的销价的变化对购运计划和总费用影响最大，哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大，并给出相应 的数字结果。

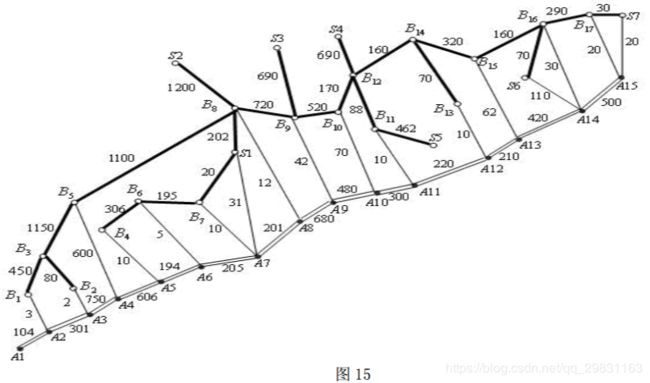
（3）如果要铺设的管道不是一条线，而是一个树形图，铁路、公路和管道构成网 络，请就这种更一般的情形给出一种解决办法，并对图 15 按（1）的要求给出模型和结果。

2 模型的建立与求解

2.1 运费矩阵的计算模型

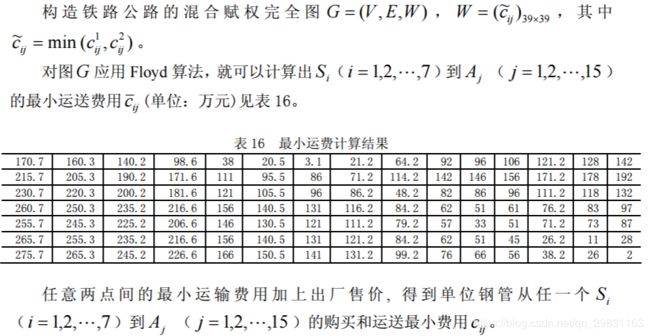
由于铁路运费不是连续的，故不能直接用 Floyd 算法来计算最小运输费用。但可以 用 Floyd 算法来计算任意两点间的最短铁路距离值，再依据题中的铁路运价表，来计算 最小运输费用。这就巧妙的避开铁路运费不是连续的问题。最终计算出铁路任意两点间 的最小运输费用  。其中，路径值无穷大时的费用也为无穷大。

②计算公路任意两点间的最小运输费用

依据题中“公路运输费用为 1 单位钢管每公里 0.1 万元（不足整公里部分按整公里 计算）”，计算出公路任意两点间的最小运输费用 。路径值为无穷大时的费用也为无 穷大。

③计算任意两点间的最小运输费用

由于可以用铁路、公路交叉运送，所以任意相邻两点间的最小运输费用为铁路、公 路两者最小运输费用的最小值。

2.2 总费用的数学规划模型

分析题目可以知道约束条件应包括： 钢厂产量约束：上限和下限（如果生产的话）；

2.3 Lingo代码

 使用计算机求解上述数学规划时，需要对约束条件（20）进行处理。我们引进0 −1 变量

利用 Lingo 求得总费用的最小值为 127.8632 亿。Lingo 程序如下：

model:
sets:
!nodes 表示节点集合;
nodes /S1,S2,S3,S4,S5,S6,S7,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A14,A15,
B1,B2,B3,B4,B5,B6,B7,B8,B9,B10,B11,B12,B13,B14,B15,B16,B17/;
!c1(i,j)表示节点 i 到 j 铁路运输的最小运价（万元）,c2(i,j)表示节点 i 到 j 公路运输的费
用邻接矩阵，c(i,j)表示节点 i 到 j 的最小运价，path 标志最短路径上走过的顶点;
link(nodes, nodes): w, c1,c2,c,path1,path;
supply/S1..S7/:S,P,f;
need/A1..A15/:b,y,z; !y 表示每一点往左铺的量，z 表示往右铺的量;
linkf(supply, need):cf,X;
endsets
data:
S=800 800 1000 2000 2000 2000 3000;
P=160 155 155 160 155 150 160;
b=104,301,750,606,194,205,201,680,480,300,220,210,420,500,0;
path1=0; path=0; w=0; c2=0;
! 以下是格式化输出计算的中间结果和最终结果; 
@text(MiddleCost.txt)=@writefor(supply(i): @writefor(need(j): @format(cf(i,j),' 6.1f' )),
@newline(1));
@text(Train_path.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path1(i,j),'5.0f')),
@newline(1));
@text(Final_path.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),'5.0f')),
@newline(1));
@text(FinalResult.txt)=@writefor(supply(i):@writefor(need(j):@format(x(i,j),'5.0f')),
@newline(1) );
@text(FinalResult.txt)=@write(@newline(1));
@text(FinalResult.txt)=@writefor(need:@format(y,'5.0f') );
@text(FinalResult.txt)=@write(@newline(2));
@text(FinalResult.txt)=@writefor(need:@format(z,'5.0f') );
enddata
calc:
!输入铁路距离邻接矩阵的上三角元素;
w(1,29)=20;w(1,30)=202;w(2,30)=1200;w(3,31)=690;w(4,34)=690;w(5,33)=462;
w(6,38)=70;w(7,39)=30;w(23,25)=450;w(24,25)=80;w(25,27)=1150;w(26,28)=306;
w(27,30)=1100;w(28,29)=195;w(30,31)=720;w(31,32)=520;w(32,34)=170;w(33,34)=88;
w(34,36)=160;w(35,36)=70;w(36,37)=320;w(37,38)=160;w(38,39)=290;
@for(link(i,j): w(i,j) = w(i, j)+w(j,i) ); !输入铁路距离邻接矩阵的下三角元素;
@for(link(i,j)|i#ne#j: w(i,j)=@if(w(i,j) #eq# 0, 20000,w(i,j))); ! 无铁路连接，元素为充分
大的数;
!以下就是最短路计算公式（Floyd-Warshall 算法）;
@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(w(i,j),w(i,k)+w(k,j));
path1(i,j)=@if(w(i,j)#gt# tm,k,path1(i,j));w(i,j)=tm)));
!以下就是按最短路 w 查找相应运费 C1 的计算公式;
@for(link|w#eq#0: C1=0);
@for(link|w#gt#0 #and# w#le#300: C1=20);
@for(link|w#gt#300 #and# w#le#350: C1=23);
@for(link|w#gt#350 #and# w#le#400: C1=26);
@for(link|w#gt#400 #and# w#le#450: C1=29);
@for(link|w#gt#450 #and# w#le#500: C1=32);
@for(link|w#gt#500 #and# w#le#600: C1=37);
@for(link|w#gt#600 #and# w#le#700: C1=44);
@for(link|w#gt#700 #and# w#le#800: C1=50);
@for(link|w#gt#800 #and# w#le#900: C1=55);
@for(link|w#gt#900 #and# w#le#1000: C1=60);
@for(link|w#gt#1000: C1= 60+5*@floor(w/100-10)+@if(@mod(w,100)#eq#0,0,5) );
!输入公路距离邻接矩阵的上三角元素;
c2(1,14)=31;c2(6,21)=110;c2(7,22)=20;c2(8,9)=104;c2(9,10)=301;c2(9,23)=3;
c2(10,11)=750;c2(10,24)=2;c2(11,12)=606;c2(11,27)=600;c2(12,13)=194;c2(12,26)=10;
c2(13,14)=205;c2(13,28)=5;c2(14,15)=201;c2(14,29)=10;c2(15,16)=680;c2(15,30)=12;
c2(16,17)=480;c2(16,31)=42;c2(17,18)=300;c2(17,32)=70;c2(18,19)=220;c2(18,33)=10;
c2(19,20)=210;c2(19,35)=10;c2(20,21)=420;c2(20,37)=62;c2(21,22)=500;c2(21,38)=30;
c2(22,39)=20;
@for(link(i,j): c2(i,j) = c2(i,j)+c2(j,i)); !输入公路距离邻接矩阵的下三角元素;
@for(link(i,j):c2(i,j)=0.1*c2(i,j)); ! 距离转化成费用;
@for(link(i,j)|i#ne#j: c2(i,j) =@if(c2(i,j)#eq#0,10000,c2(i,j) )); !无公路连接，元素为充分
大的数; 
@for(link: C= @if(C1#le#C2,C1,C2)); ! C1 和 C2 矩阵对应元素取最小;
@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(C(i,j),C(i,k)+C(k,j));
path(i,j)=@if(C(i,j)#gt# tm,k,path(i,j));C(i,j)=tm)));
@for(link(i,j)|i #le# 7 #and# j#ge#8 #and# j#le# 22:cf(i,j-7)=c(i,j)); !提取下面二次规划模
型需要的 7×15 矩阵;
endcalc
[obj]min=@sum(linkf(i,j):(cf(i,j)+p(i))*x(i,j))+0.05*@sum(need(j):y(j)^2+y(j)+z(j)^2+z(j));
! 约束;
@for(supply(i):[con1]@sum(need(j):x(i,j))<= S(i)*f(i));
@for(supply(i):[con2]@sum(need(j):x(i,j)) >= 500*f(i));
@for(need(j):[con3] @sum(supply(i):x(i,j))=y(j)+z(j));
@for(need(j)|j#NE#15:[con4] z(j)+y(j+1)=b(j));
y(1)=0; z(15)=0;
@for(supply: @bin(f));
@for(need: @gin(y));
end 

3 管道为树形图时的模型

当管道为树形图时，建立与上面类似的非线性规划模型

用 Lingo 求解得最小费用为 140.6631 亿元。Lingo 程序如下：

model:
sets:
 ! nodes 表示节点集合;
nodes
/S1,S2,S3,S4,S5,S6,S7,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A14,A15,A16,A
17,A18,A19,A20,B1,B2,B3,B4,B5,B6,B7,B8,B9,B10,B11,B12/;
!c1(i,j)表示节点 i 到 j 铁路运输的最小单位运价（万元）,c2(i,j)表示节点 i 到 j 公路运输
的邻接权重矩阵，c(i,j)表示节点 i 到 j 的最小单位运价，path 标志最短路径上走过的顶
点;
link(nodes, nodes): w, c1,c2,c,path1,path;
supply/S1..S7/:s,p,f;
need/A1..A21/:b,y,z;!y 表示每一点往节点编号小的方向铺设量，z 表示往节点编号大的
方向铺设量;
linkf(supply, need):cf,x; 
special/1..3/:sx; ! 铺设节点 9，11，17 往最大编号节点方向的铺设量;
endsets
data:
s=800 800 1000 2000 2000 2000 3000;
p=160 155 155 160 155 150 160;
b=104,301,750,606,194,205,201,680,480,300,220,210,420,500,42,10,130,190,260,100,0;
path1=0; path=0; w=0; c2=0;
! 以下是格式化输出计算的中间结果和最终结果;
@text(MiddleCost.txt)=@writefor(supply(i): @writefor(need(j): @format(cf(i,j),' 6.1f' )),
@newline(1));
@text(Train_path.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path1(i,j),'5.0f')),
@newline(1));
@text(Final_path.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),'5.0f')),
@newline(1));
@text(FinalResult.txt)=@writefor(supply(i):@writefor(need(j):@format(x(i,j),'5.0f')),
@newline(1) );
@text(FinalResult.txt)=@write(@newline(1));
@text(FinalResult.txt)=@writefor(need:@format(y,'5.0f'));
@text(FinalResult.txt)=@write(@newline(2));
@text(FinalResult.txt)=@writefor(need:@format(z,'5.0f'));
enddata
calc:
!输入铁路距离邻接矩阵的上三角元素;
w(28,30)=450;w(29,30)=80;w(30,32)=1150;w(31,33)=306;w(33,34)=195;w(1,34)=20;
w(1,35)=202;w(32,35)=1100;w(2,35)=1200;w(23,35)=720;w(3,23)=690;w(23,36)=520;
w(36,37)=170;w(4,37)=690;w(5,24)=462;w(24,37)=88;w(25,37)=160;w(25,26)=70;
w(25,27)=320;w(27,38)=160;w(6,38)=70;w(38,39)=290;w(7,39)=30;
@for(link(i,j): w(i,j) = w(i, j)+w(j,i) );!输入铁路距离邻接矩阵的下三角元素;
@for(link(i,j)|i#ne#j: w(i,j)=@if(w(i,j) #eq# 0, 20000,w(i,j))); ! 无铁路连接，元素为充分
大的数;
!以下就是最短路计算公式（Floyd-Warshall 算法）;
@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(w(i,j),w(i,k)+w(k,j));
path1(i,j)=@if(w(i,j)#gt# tm,k,path1(i,j));w(i,j)=tm)));
!以下就是按最短路 w 查找相应运费 C1 的计算公式;
@for(link|w#eq#0: C1=0);
@for(link|w#gt#0 #and# w#le#300: C1=20);
@for(link|w#gt#300 #and# w#le#350: C1=23);
@for(link|w#gt#350 #and# w#le#400: C1=26);
@for(link|w#gt#400 #and# w#le#450: C1=29);
@for(link|w#gt#450 #and# w#le#500: C1=32);
@for(link|w#gt#500 #and# w#le#600: C1=37);
@for(link|w#gt#600 #and# w#le#700: C1=44);
@for(link|w#gt#700 #and# w#le#800: C1=50);
@for(link|w#gt#800 #and# w#le#900: C1=55);
@for(link|w#gt#900 #and# w#le#1000: C1=60);
@for(link|w#gt#1000: C1= 60+5*@floor(w/100-10)+@if(@mod(w,100)#eq#0,0,5) );
!输入公路距离邻接矩阵的上三角元素;
c2(8,9)=104;c2(9,10)=301;c2(10,11)=750;c2(11,12)=606;c2(12,13)=194;c2(13,14)=205;
c2(14,15)=201;c2(15,16)=680;c2(16,17)=480;c2(16,23)=42;c2(17,18)=300;c2(18,19)=220; 
c2(18,24)=10;c2(19,20)=210;c2(20,21)=420;c2(21,22)=500;c2(24,25)=130;c2(24,26)=190;
c2(26,27)=260;c2(6,27)=100;c2(9,28)=3;c2(10,29)=2;c2(11,32)=600;c2(12,31)=10;
c2(13,33)=5;c2(14,34)=10;c2(1,14)=31;c2(15,35)=12;c2(17,36)=70;c2(19,26)=10;
c2(20,27)=62;c2(6,21)=110;c2(21,38)=30;c2(22,39)=20;c2(7,22)=20;
@for(link(i,j): c2(i,j) = c2(i,j)+c2(j,i)); !输入公路距离邻接矩阵的下三角元素;
@for(link(i,j):c2(i,j)=0.1*c2(i,j)); ! 距离转化成费用;
@for(link(i,j)|i#ne#j: c2(i,j) =@if(c2(i,j)#eq#0,10000,c2(i,j) )); ! 距离转化成费用;
@for(link: C= @if(C1#le#C2,C1,C2)); !邻接矩阵的对角线元素变为 0;
@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(C(i,j),C(i,k)+C(k,j));
path(i,j)=@if(C(i,j)#gt# tm,k,path(i,j));C(i,j)=tm)));
@for(link(i,j)|i #le# 7 #and# j#ge#8 #and# j#le# 27:cf(i,j-7)=c(i,j)); !提取下面二次规划模
型需要的 7×21 矩阵;
@for(supply(i):cf(i,21)=c(i,6));
endcalc
[obj]min=@sum(linkf(i,j):(cf(i,j)+p(i))*x(i,j))+0.05*@sum(need(j):y(j)^2+y(j)+z(j)^2+z(j))+
0.05*@sum(special:sx^2+sx);
! 约束;
@for(supply(i):[con1]@sum(need(j):x(i,j))<= s(i)*f(i));
@for(supply(i):[con2]@sum(need(j):x(i,j)) >= 500*f(i));
@for(need(j)|j#ne#9 #and# j#ne#11 #and# j#ne#17:[con3] @sum(supply(i):x(i,j))=y(j)+z(j));
y(9)+z(9)+sx(1)=@sum(supply(i):x(i,9)); y(11)+z(11)+sx(2)=@sum(supply(i):x(i,11));
y(17)+z(17)+sx(3)=@sum(supply(i):x(i,17));
@for(need(j)|j #le# 14:(z(j)+y(j+1))=b(j));
@for(need(j)|j#ge#19 #and# j#le#20:z(j)+y(j+1)=b(j));
sx(1)+y(16)=42; sx(2)+y(17)=10; sx(3)+y(19)=190; z(17)+y(18)=130;
y(1)+z(15)+z(16)+z(18)+z(21)=0;
@for(supply: @bin(f)); @for(need: @gin(y));
end 

---

【1】图与网络模型及方法：图与网络的基本概念

【2】图&网络模型应用—最短路径问题

【3】树：基本概念与最小生成树

【4】匹配问题： 匈牙利算法 、最优指派、相等子图

【5】Euler 图和 Hamilton 图

【6】计划评审方法和关键路线法【统筹方法】：广泛地用于系统分析和项 目管理

【7】最小费用流及其求法 ：

【8】最大流问题  

【10】钢管订购和运输问题

---