Mathematica画图的问题
由于写论文,使用了mathematica软件,从入门到写作,着实费了很多功夫,总结下自己遇到的问题,以后便于查看。
一 首先是书写函数问题
函数和MATLAB不一样,使用方括号"[]",而不是圆括号。
在进行求指数问题时,我总是会写成Exp()的形式,结果解出来的结果却还有Exp,我当时很纳闷,才明白过来。这点让我半天的代码白费了,这个和画图关系不大,可以暂时略过。
二 画图多个图怎么放在一个画布里以及散点图的问题
这个很简单,使用一个简单的函数就解决了。可以看例子:
Show[Plot[x^2, {x, 0, 3.5}], Plot[x^3, {x, 0, 3.5}]]
这里面使用了两个Plot函数,画两个图,然后放在show函数里面就可以了。当然也可以拆开写成如下形式:
p1=Plot[x^2, {x, 0, 3.5}];
p2=Plot[x^3, {x, 0, 3.5}];
Show[p1,p2]
两者的效果是一样的,其中 {x, 0, 3.5}表示坐标x的取值范围在0-3.5之间,我们输出的图片如下图所示。
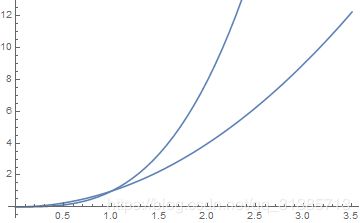
如果想画散点图,则也可以和散点图组合,组合的方式如下:
Show[Plot[x^2, {x, 0, 3.5}], Plot[x^3, {x, 0, 3.5}], ListPlot[{1, 4, 9}]]
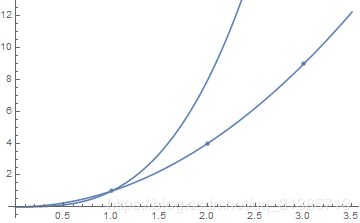
ListPlot[{1, 4, 9}]就是所要的散点图,但是这里默认的1,4,9三个值的坐标是(1,1),(2,4),(3,9),如果自己想重新定义坐标轴,不按照默认的来,则需要这样定义:
data = {{1, 2}, {2, 4}, {2, 6}};
ListPlot[data, PlotStyle -> {Red, PointSize[Large]}]
代码中data就是定义的坐标集,得出来的结果就是对应的坐标,结果如下图所示,为了明显我把坐标描红表示, PlotStyle -> {Red, PointSize[Large]}是我设计的显示样式,为红色大圆点。
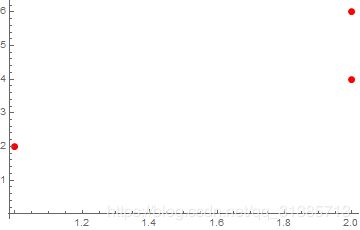
这个是组合图的基本画法以及散点图的个性化画法
三 如何设置坐标轴的范围
我们常常需要根据自己的要求设计x轴和y轴的范围,而mathmatica往往不会随着你的心思走,所以自己也可以调,主要为下:
p = x^2 + Sin[x] - 4;
Plot[p, {x, 0, 10}, PlotRange -> {0, 50}]
在上述代码中, {x, 0, 10}定义了x的取值范围, PlotRange -> {0, 50}定义了y的取值范围,则画图如下:

四 美化问题:线型、坐标轴比例、标签
1 线型问题
线型主要考虑线的颜色、粗细还有线的样式,这里都需要样式的问题,我直接上代码,可以慢慢体会:
p1 = x*2 - 10;
p2 = x + 2 - 10;
p3 = x^2 - 10;
p4 = x^3 - 10;
p5 = x^4 - 4;
b1 = Plot[p1, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Black, Thin}];
b2 = Plot[p2, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Blue, Dotted}];
b3 = Plot[p3, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Red, DotDashed}];
b4 = Plot[p4, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Green, Thick}];
b5 = Plot[p5, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Orange, Dashed}];
Show[b1, b2, b3, b4, b5]
代码里我设置了五个函数,然后放在show函数里一起展示他们的图像,其中PlotStyle -> {Black, Thin}里的两个参数分别定义了线的颜色和线的类型,可以看一下具体的效果:
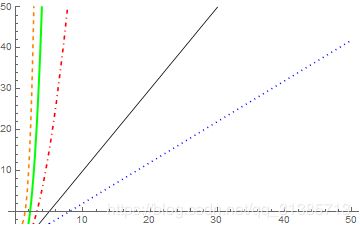
2 坐标轴比例问题
mathematica默认的坐标轴是扥比例的,如果不是的话,会根据取值范围调,当然如果自己不满意,也可以自己亲自去调,代码很简单如下:
SetOptions[Plot, AspectRatio -> 4]
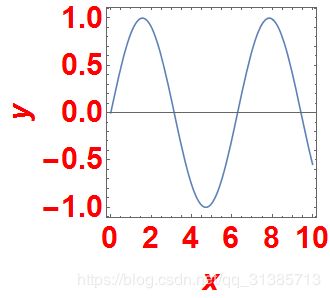
Plot[2 Sin[x], {x, 0, 10}]
在代码中SetOptions[Plot, AspectRatio -> 4]可以绘制宽高比,AspectRatio -> 4即为宽高比,我们看一下更改比例后的图片如何:
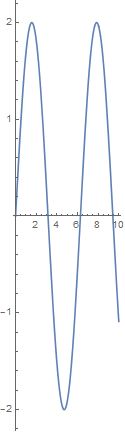
这里显示的是有些夸张了,是为了更加明显表达比例的使用。
3 标签
标签涉及到的问题有:
- 坐标轴:x,y标签的大小问题,以及位置放置问题
- 坐标轴刻度:刻度值大小、颜色的问题
首先把mathmatica的x,y轴位置放置、坐标轴刻度的问题放在一起讲,看代码:
Plot[3 Sin[x], {x, 0, 10},
AxesLabel -> {x, y},
AxesStyle -> Directive[Gray, FontSize -> 30],
TicksStyle -> Orange]
这里为了好理解,分段写了一下,AxesLabel -> {x, y}, 定义了坐标轴的标签名分别是x和y,当然自己也可以改,改成人数和成本,时间和效用都是可以的。
AxesStyle -> Directive[Gray, FontSize -> 30],定义了坐标轴标签的颜色和字体大小
TicksStyle -> Orange这里定义了坐标刻度的颜色,我们可以看一下结果:
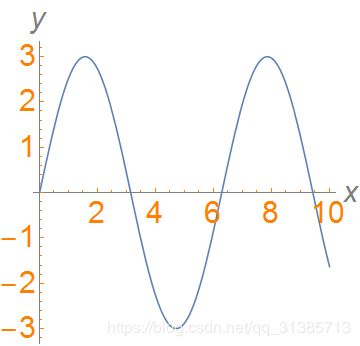
当然有时候如果我们坐标的标签非常的长,我们不希望坐标轴标签放在坐标的两端,而是居中的位置,把坐标轴标签居中放置,需要使用到Frame的知识,但是使用它的时候,标签内部好像就不能显示了,这个我是亲身尝试过的,在这里整体演示一遍代码如下:
Plot[Sin[x], {x, 0, 10},
Frame -> {{True, False}, {True, False}},
FrameLabel -> {x, y},
LabelStyle -> Directive[Red, Bold, 30]]
代码中定义了Frame和FrameLable两个变量,他们两个可以算是共生关系。
为何这么说呢,Frame意为边框,实则在定义的时候上下左右像相框一样把图形包起来,如果你不想要哪个相框,你就把它定义为False,在这里 {{True, False}, {True, False}}分别指{{下真,上假},{左真,右假}},所以是正常的x轴和y轴都有显示,而x,y就对应的是边框标签的值,这个标签和坐标轴标签不是一个意思,要区分开。显示的结果如下所示:
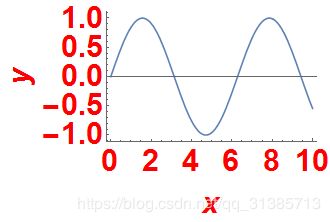
这里可以看到只有左边和下边有边框,上边和下边没有边框,边框分别显示了x和y的字样,是我们定义的。
也可以看一下如果四个框都显示出来的效果,先写代码:
Plot[Sin[x], {x, 0, 10}, Frame -> {{True, True}, {True, True}},
FrameLabel -> {x, y}, LabelStyle -> Directive[Red, Bold, 30]]
五 图例问题
画图时,如果遇到多条曲线相交的时候,每条图像的出现往往会让读者产生疑惑,此时需要对每一条加以解释,这时候需要加图例。加图例的代码也很简单,如下代码;
p1 = x*2 - 10;
p2 = x + 2 - 10;
p3 = x^2 - 10;
p4 = x^3 - 10;
p5 = x^4 - 4;
a1 = Plot[p1, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Thin}, PlotLegends -> {"ONE"}];
a2 = Plot[p2, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Dotted}, PlotLegends -> {"two"}];
a3 = Plot[p3, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, DotDashed}, PlotLegends -> {"three"}];
a4 = Plot[p4, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Thick}, PlotLegends -> {"four"}];
a5 = Plot[p5, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Dashed}, PlotLegends -> {"five"}];
Show[a1, a2, a3, a4, a5, AxesLabel -> {"time", "usage"}, TicksStyle -> Directive[Black, 12]]
在这里 PlotLegends -> {“five”}定义的就是图例,图例里面的字符串就是要说明的内容,我们看一下结果图:
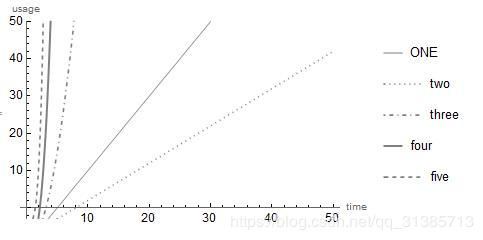
在右方可以看到对每一条线都出现了解释,图例就生成了。
然而在生成图例的时候,mathematica默认图例不和图形在一起,就是如果输出为图片的话,图例是分开的部分,不会输出,这时候就需要把图例变成图像的一部分,我们需要进行如下的操作:
p1 = x*2 - 10;
p2 = x + 2 - 10;
p3 = x^2 - 10;
p4 = x^3 - 10;
p5 = x^4 - 4;
a1 = Plot[p1, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Thin}, PlotLegends -> Placed[{"ONE"}, Riffle]];
a2 = Plot[p2, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Dotted}, PlotLegends -> Placed[{"TWO"}, Riffle]];
a3 = Plot[p3, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, DotDashed},PlotLegends -> Placed[{"three"}, Riffle]];
a4 = Plot[p4, {x, 0, 50}, PlotRange -> {-3, 50}, PlotStyle -> {Gray, Thick}, PlotLegends -> Placed[{"four"}, Riffle]];
a5 = Plot[p5, {x, 0, 50}, PlotRange -> {-3, 50},
PlotStyle -> {Gray, Dashed}, PlotLegends -> Placed[{"five"}, Riffle]];
Show[a1, a2, a3, a4, a5, AxesLabel -> {"time", "usage"}, TicksStyle -> Directive[Black, 12]]
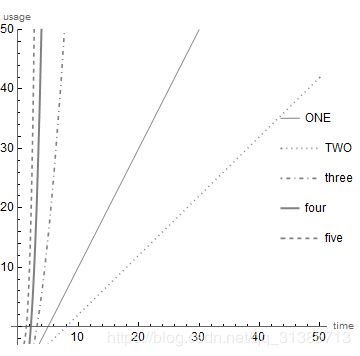
可以看到此时图例跑到图的里面去了,而代码只是在PlotLegends 后面使用了Placed函数,这个函数可以设置图例的放置方式,Riffle是指交互插入,如果设置成Top、Center、Right、Left也是可以的,这时好像就不是在图形里面了,可以自己尝试一下。
六 分段函数
这个比较简单,和MATLAB很像,所以直接上代码,可以自己慢慢体会。
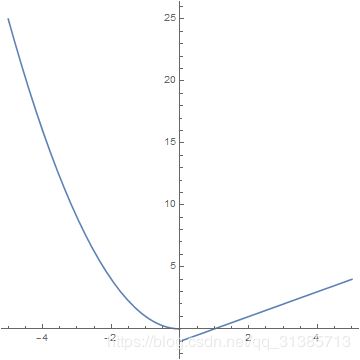
y = If[x >= 0, x - 1, x^2];
Plot[y, {x, -5, 5}]