Python遗传算法框架使用实例（二）多目标优化问题Geatpy for Python与Matlab的对比学习

在前面几篇文章中，我们已经介绍了高性能Python遗传和进化算法框架——Geatpy的使用及一些案例。

https://blog.csdn.net/qq_33353186/article/details/82014986

https://blog.csdn.net/qq_33353186/article/details/82020507

https://blog.csdn.net/qq_33353186/article/details/82047692

详细的Geatpy官方教程文档在官网可以查看：

http://geatpy.com/index.php/geatpy%E6%95%99%E7%A8%8B/

本篇就一个多目标优化实例进行展开讲述，并且与使用Matlab工具箱进行对比：

回顾一下更新方法：

pip install --upgrade --user geatpy

下面对一个两个目标的最小化问题进行求解：

先用Geatpy尝试求解，先定义问题类MyProblem，然后编写执行代码直接套用内置的moea_nsga2_templet进化算法模板对问题进行求解：

# -*- coding: utf-8 -*-
import numpy as np
import geatpy as ea
"""
问题类定义
"""
class MyProblem(ea.Problem): # 继承Problem父类
    def __init__(self):
        name = 'MyProblem' # 初始化name（函数名称，可以随意设置）
        # 定义需要匹配的句子
        M = 2 # 初始化M（目标维数）
        maxormins = [1] * M # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 2 # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [-5] * Dim # 决策变量下界
        ub = [5] * Dim # 决策变量上界
        lbin = [1] * Dim # 决策变量下边界
        ubin = [1] * Dim # 决策变量上边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
    def aimFunc(self, pop): # 目标函数
        x1 = pop.Phen[:, [0]]
        x2 = pop.Phen[:, [1]]
        pop.ObjV = np.zeros((pop.Phen.shape[0], self.M))
        pop.ObjV[:,[0]] = x1**4-10*x1**2+x1*x2+x2**4-x1**2*x2**2
        pop.ObjV[:,[1]] = x2**4-x1**2*x2**2+x1**4+x1*x2
"""
执行脚本
"""
if __name__ == "__main__":
    """================================实例化问题对象============================="""
    problem = MyProblem()     # 生成问题对象
    """==================================种群设置================================"""
    Encoding = 'RI'           # 编码方式
    NIND = 1000               # 种群规模
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # 创建区域描述器
    population = ea.Population(Encoding, Field, NIND) # 实例化种群对象（此时种群还没被初始化，仅仅是完成种群对象的实例化）
    """=================================算法参数设置=============================="""
    myAlgorithm = ea.moea_NSGA2_templet(problem, population) # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 100  # 最大进化代数
    """============================调用算法模板进行种群进化========================="""
    NDSet = myAlgorithm.run() # 执行算法模板，得到帕累托最优解集NDSet
    NDSet.save()              # 把结果保存到文件中
    # 输出
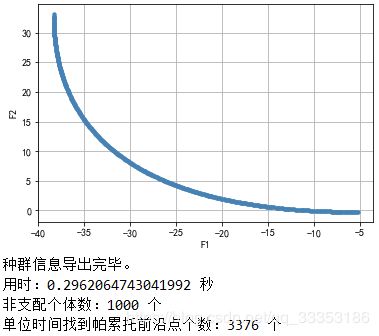
    print('用时：%s 秒'%(myAlgorithm.passTime))
    print('非支配个体数：%s 个'%(NDSet.sizes))
    print('单位时间找到帕累托前沿点个数：%s 个'%(int(NDSet.sizes // myAlgorithm.passTime)))

执行结果如下：

其中moea_nsga2_templet的算法模板源代码可以参见：

https://github.com/geatpy-dev/geatpy/blob/master/geatpy/templates/moeas/nsga2/moea_NSGA2_templet.py

代码有详细注释，可以清晰看到多目标优化NSGAII算法的详细流程。

下面将用Matlab的遗传算法工具箱进行对比实验：

clc,clear
% 定义目标函数
fun1 = @(x) x(1)^4-10*x(1)^2+x(1)*x(2)+x(2)^4-x(1)^2*x(2)^2; %min f1(x1,x2)
fun2 = @(x) x(2)^4-x(1)^2*x(2)^2+x(1)^4+x(1)*x(2); %min f2(x1,x2)

aimfuc = @(x) [fun1(x) fun2(x)]; %获取目标函数句柄
nvars=2;      %变量个数
lb=[-5,-5];   %下限
ub=[5,5];     %上限
A=[];b=[];    %线性不等式约束
Aeq=[];beq=[];%线性等式约束
tic           %开始计时
options=gaoptimset('paretoFraction',1,'populationsize',1000,'generations',100,'stallGenLimit',1,'TolFun',1e-100);
[x,fval] = gamultiobj(aimfuc,nvars,A,b,Aeq,beq,lb,ub,options);
time = toc    %结束计时
plot(fval(:,1),fval(:,2),'k.') %绘图
fprintf('找到的前沿点数： %d\n', size(fval,1));
fprintf('平均每秒找到的前沿点数： %f\n', size(fval,1)/time);

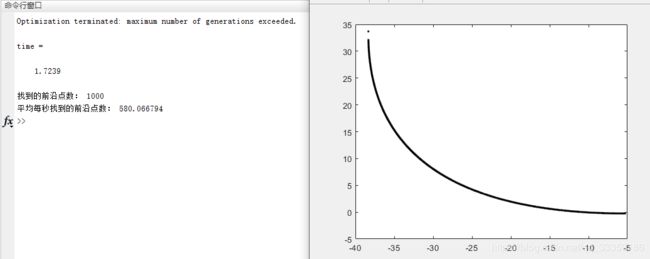
执行结果如下：

对比发现Geatpy的效率比Matlab高出了一个数量级。尝试增大所需要搜索的帕累托前沿点的数量，Matlab变慢了一个数量级，而Geatpy的耗时基本稳定。如果把上面的1000个个体改为1万，则Python耗时13.3秒，Matlab耗时55.25秒：

除了NSGA-II算法外，Geatpy还支持适应性权法重法(awGA)、随机权重法(rwGA)、NSGA-III、RVEA等。除了多目标优化，Geatpy还支持单目标优化、差分进化、组合优化、复杂约束优化、混合编码优化等。相应的算法均整合在算法模板内，源代码参见：

https://github.com/geatpy-dev/geatpy/tree/master/geatpy/templates

欢迎继续跟进，感谢！