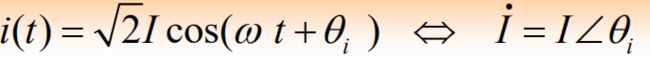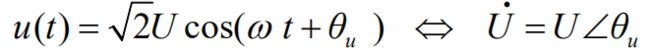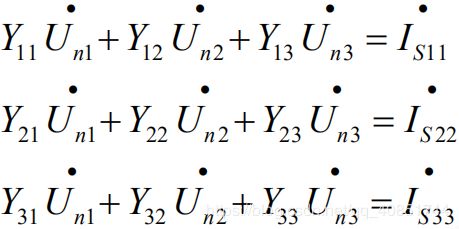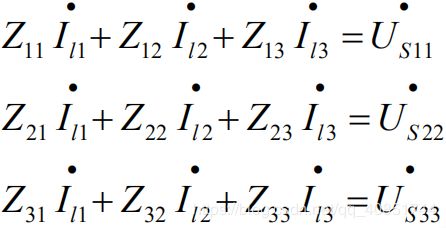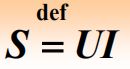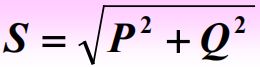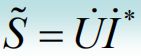电路分析期末总结
本人正好在准备第九周的期中考试,在复习时写出这个总结,仅为准备考试使用,逻辑线不强,记录一下自己的学习历程,有很多的个人见解,谨慎阅读。
一、集总参数电路中电压与电流的约束关系:
1、关联参考方向
电流参考方向与电压参考方向一致。其中电压的参考方向是由(+)指向(-)。在计算题目的时候需要规定好所有的元件的电压与电流的方向,计算出来的数值(无论正负)才有意义。
所有关联方向下的物理定律都是正的(原本样式),而在非关联参考方向下的物理定律都是负的(加一个负号)。
在关联参考方向下,计算得到的功率为吸收功率,加个负号后才是输出功率。电阻的功率一定为正,源的功率可能为负。
2、KCL
对于任意集总电路中的任意节点(广义),在任意时刻,流入和流出的电流相等。表达了电路中各支路电流间的约束关系。由电荷守恒推出。
3、KVL
对于任意集总电路中的任意回路(广义,可为假想回路),在任意时刻回路上的电压降之和为0.表达了电路中各支路电压间的约束关系。由能量守恒推出。
4、电流源、电压源、受控源
与电路平行为电压源,与电路垂直为电流源,菱形为受控源。受控源在处理的时候直接当成独立源(电压源或电流源)带入KCL或KVL即可
5、分压分流公式
初高中时学到的串联分压,并联分流,电阻等效公式。注意:首尾相连即为串联(两者之间不能有支路);首首、尾尾分别相连即为并联(可有支路,但要注意合并后的电阻连接方式)
6、等效规律
(1)两电压源串联:电压相加
(2)两电流源并联:电流相加
(3)两电压源并联:无效,违背KVL
(4)两电流源串联:无效,违背KCL
(5)电压源与电阻并联:可等效为电压源,端口电压等于电压源电压
(6)电流源与电阻串联:可等效为电流源,端口电流等于电流源电流
(7)电压源与电阻串联:与电流源和电阻并联相互等效,电阻大小不变,U=IR,转换时注意转换后独立源产生的电流方向与原先相同。
(8)电流源与电压源同时存在:将其中一个通过(7)转换成电流/电压源后进行化简
二、网孔分析和节点分析
1、网孔分析
针对一个多孔线性电路,对于每一个网孔可以列出一个KVL方程,其中每个电阻元件的电压通过VCR求得。如果有电流源I则转换为一电压为u的电压源,u为假设的变量,并添加一关于电流I的辅助方程。
将受控源当成独立源,同样进行代入与化简,再将控制量用网孔电流表示
2、互易定理
在只含一个电压源,不含受控源的线性电阻电路中如果在某一支路中x的电压源us在另一支路y上产生电流i,则将电压源转移到支路y后将会在支路x上产生电流i
3、节点分析
针对一个多孔线性电路,对于每一个节点可以列出一个KCL方程,其中每条支路上的电流通过该支路上的某个电子元件的VCR求得。如果有电压源u则转换为电流源i,i为假设的变量,并添加一关于电压u的辅助方程。
将受控源当成独立源,同样进行代入与化简,再将控制量用网孔电流或电压表示
4、运算放大器(不考)
只需要记住,对于理想的运放(就是题目中的运放),有虚短(负极的电流等于正极的电流)与虚断(负极的电压降等于正极的电压降)两个特性即可解决所有的问题。
三、叠加方法与网络函数:
1、网络函数
所谓激励就是独立电流源、电压源(以及受控源)
所谓响应就是电路在激励作用下产生的电流与电压
两者永远成正比关系,即网络函数H=响应/激励。对任何线性电阻电路,网络函数都是实数。
2、叠加定理
在线性电路中,任一支路的响应可以看成是电路中每一个独立电源作用于电路时所产生的的响应的代数和。实际上就是将原本的多源电路拆分成多个单源电路,分别计算每个单源电路在某一元件上产生的响应,将所有的响应求代数和即可得到原电路对该元件产生的响应。
注意,其余电源置零意味着电压源作为导线短路,电流源作为断口开路。
叠加时注意各分量的参考方向。
如果含有受控源则进行保留处理。
四、分解方法及单口网络
1、置换定理
对于给定的电路,如果某一支路(广义)的电压为u,电流为i,则可替换为电压为u的电压源或者电流为i的电流源或者电阻为r=u/i的电阻元件。原理是电路的KCL和KVL不变。
置换定理对线性、非线性电路均使用。
置换后的电路必须只有唯一解(KCL,KVL为确定的数,不是电流相互相关的方程组)
2、戴维南定理
线性有源二端网络可等效为一电压源与一电阻串联的电路,电压源电压为单口网络开路电压,电阻为所有源置零后的等效电阻。注意,受控源不作处理,进行保留;要求转换后的电路在外部元件上产生的电流方向不变。
3、诺顿定理
线性有源二端网络可等效为一电流源与一电阻并联的电路,电流源电流为单口网络短路电流,电阻为所有源置零后的等效电阻。注意,受控源不作处理,进行保留;要求转换后的电路在外部元件上产生的电流方向不变。
4、开路短路法
先将单口网络短路,通过KCL和KVL求得当前的流过外支路的电流,再进行断路,通过KCL和KVL求得当前支路两端的电压。注意,此时所有的源均进行保留。电阻等于所求的电压与电流的比值
5、外加电源法
先将单口网络中的独立源(不包括受控源)置零,然后在端口上加上一外电压u,通过KCL和KVL求出在外支路上的电流I,则R=U/I。此时U为我们假设的一个数值,不为零且随意。
6、最大功率传递定理
对于戴维南或诺顿等效电路,当负载满足RL=R的时候,负载会火的最大功率,此时称为最大功率匹配,而最大功率为U^2/(4*R),而在一般情况为下式:
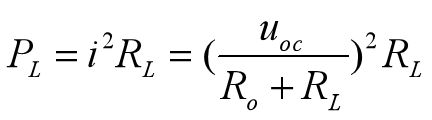
五、电容元件和电感元件
动态元件,伏安关系为微分关系
1、电容元件
当稳定时,相当于开路。
一种储能元件,电导体由绝缘材料分开就能产生电容,C=Q/U
可以阻断直流,本身不消耗能量
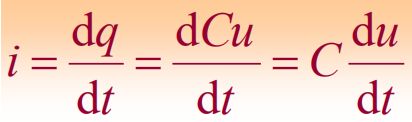
电流大小取决于电压变化率,由此导致电压不能够突变,必须为时间的连续函数
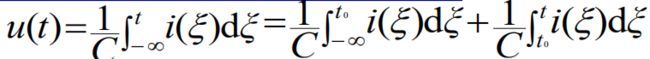
某一时刻的电容电压值与-∞到该时刻的所有电流值有关,即电容元件有记忆电流的作用,注意是否为关联方向。
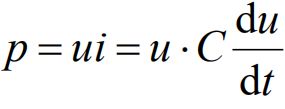
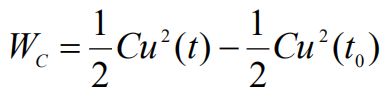
电容的储能只与当时的电压值有关,电容储能不能跃变,反映了电压不能跃变, 电容储存的能量一定大于或等于零。
2、电感元件
当稳定时,相当于短路。
一种抵抗电流变化、储存磁能的部件,L=φ/I
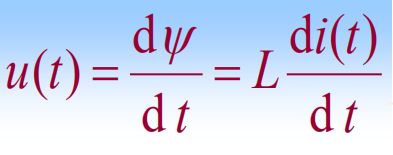
电压大小取决于电流变化率,由此导致电流不能够突变,必须为时间的连续函数,I的公式如下
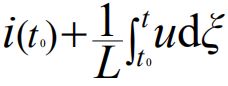
某一时刻的电感电流值与-∞到该时刻的所有电流值有关,即电感元件有记忆电压的作用,电感元件也是记忆元件。
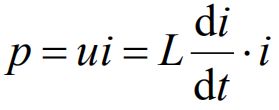
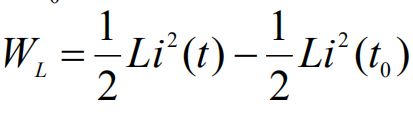
电感的储能只与当时的电流值有关,电感电流不能跃变,反映了储能不能跃变,电感储存的能量一定大于或等于零。
3、电容与电感的对偶性

电容对应电感
电容电压对应电感电流
电容电流对应电感电压
公式同理
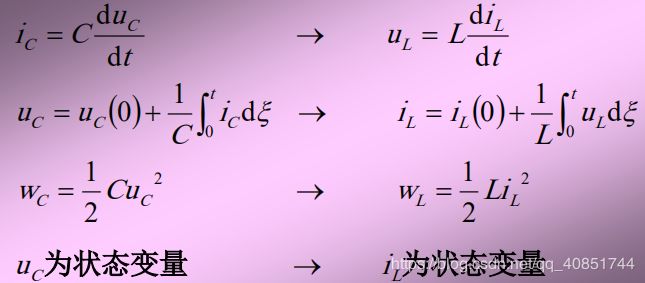
由此可知:
电容串联:电容的倒数之和,相当于间隙变宽了
电容并联:电容之和,相当于极板变大了
电感串联:电感之和,相当于变长了
电感并联:电感倒数之和,相当于横截面变大了
六、一阶电路
1、初始条件:
f(0-)从无限小向0时逼近,f(0+)从无限大向0逼近
2、环路定理:
换路瞬间,电容的电压和电荷不会发生突变,电感的电流和磁道不会发生突变
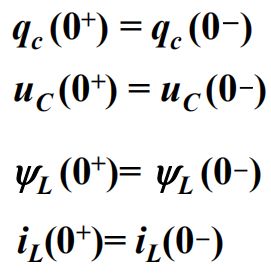
个人理解:
①0-时刻,电容视为开路,电感视为短路,用KCL和KVL计算两端电压u与通过电流i;
②0+时刻,电容视为u的电压源,方向不变;电感视为i的电流源,方向不变
3、求初始值的步骤
①由换路前电路(一般为稳定状态)求uC(0-)和iL(0-);
②由换路定律得 uC(0+) 和 iL(0+)。
③画0+等效电路。
a. 换路后的电路
b. 电容(电感)用电压源(电流源)替代。(取0+时刻值,方向与原假定的电容电压、电感电流方向相同)
④由0+电路求所需各变量的0+值。
4、零输入响应
变化量(C的电压,L的电流)通解公式:
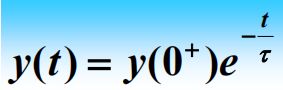
其中,RC电路的时间常数为τ=RC,RL电路的时间常数为τ=L/R
能量为:
①RC电容电路:W=1/2CU2
②RL电感电路:W=1/2LI2
5、零状态响应
变化量(C的电压,L的电流)通解公式:
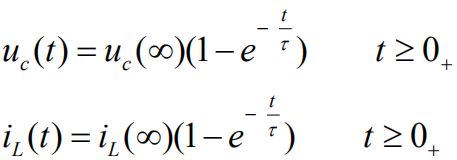
其中,RC电路的时间常数为τ=RC,RL电路的时间常数为τ=L/R
能量为:
①RC电容电路:W=1/2CU2
②RL电感电路:W=1/2LI2
6、全响应
记住,只要记住三要素公式,就可以求以上三种状态的变化量的瞬时状态,也就是三要素共识是一阶电路的通解
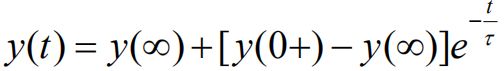
三要素为:
①初始值y(0+),通过0-电路得到初始u或i,然后通过初始u或i得到0+电路之后求得(实际上,由于换路定理,基本上得到0-电路之后就可以得到相应变量的初始值0+了)
②稳态值y(∞),通过0+电路得到∞时的稳定电路得到
③时间常数,RC电路为τ=RC,RL电路为τ=L/R
记住,做题的时候,一定要画图!!!
八、阻抗和导纳
瞬时值:小写u,i
有效值:大写U,I
最大值:大写加下表Um,Im,为有效值的1.414倍
复数、相量:大写加点U`
相位差:两个同频率正弦量的相位之差
交流电功为积分
1、复数
A=a+bj,而又因为A=|A|ejθ,其中θ为arctan(b/a)
通过将A化为三角函数式可以有A=|A|(cosθ+jsinθ)=a+bj=|A|∠θ,可以看到,我们可以将一个正弦量与一个复数的实部联系起来
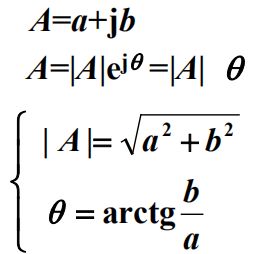
复数运算:
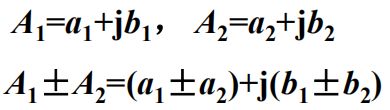
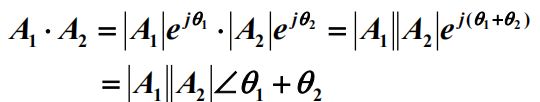
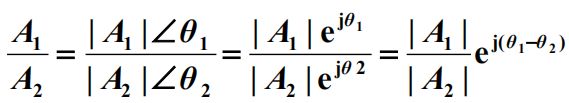
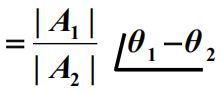
加减:实部虚部相加减
乘法:模相乘,角相加
除法:模相除,角相减
把 ejθ称为旋转因子,=cosθ +jsinθ =1∠θ,相当于把A顺时针旋转θ度,有几个特殊的;
①θ为π/2的时候,为j
②θ为-π/2的时候,为-j
③θ为±π的时候,为-1
对于正弦电,可有:i(t)=Imcos(ωt+θ)=Re[Ime(jωt+θ)]=Re[Im`ejωt]
此时可有等式:
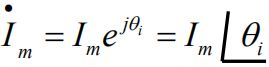
2、相量法的应用
①电阻元件VCR的相量形式:
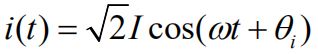
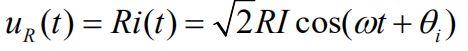
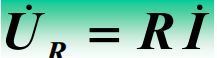
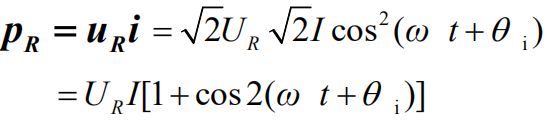
相当于电流与电压同相位
②电感元件VCR的相量形式
![]()
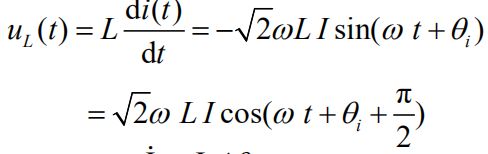
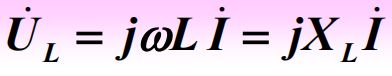

电感的电压领先电流90°
③电容元件VCR的相量形式:
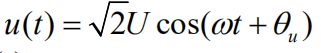
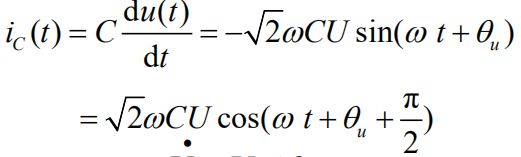

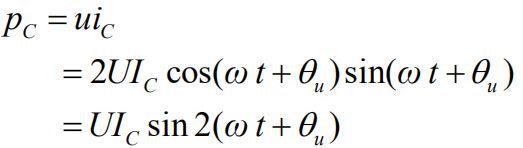
电流领先电压90°
④基尔霍夫定律的相量形式
KCL:
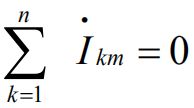
KVL:
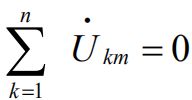
3、阻抗与导纳
说白了,就是加入了电感和电容这两个动态元件之后,对电阻这个含义的扩充。
阻抗:正弦交流电路中元件的电压相量与电流相量之比
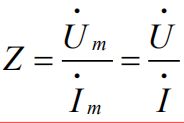
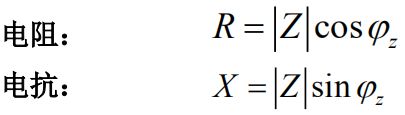
阻抗的模就是U/I,即电压的有效值/电流的有效值
电阻:
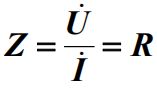
电容:
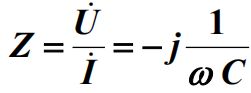
电感:
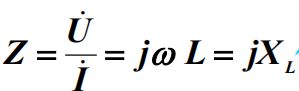
RLC串联电路:
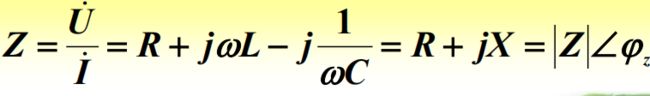
虚部为正是感性电路,电压领先;虚部为负是容性电路,电流领先
导纳:阻抗的倒数,Y,适用于RLC并联电路
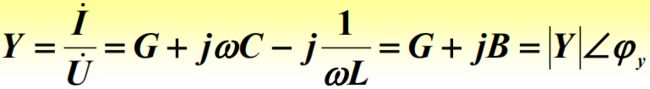
串联电路里,Z=Z1+Z2,并联电路里,1/Z=1/Z1+1/Z2
在计算正弦稳态电路的时候,需要将时域模型(u(t))转化为相量模型,并画出对应的相量图
R转化为R,L转换为jωL,C转换为1/jωC,电压转换为电压相量,电流转化为电流向量
九、正弦稳态功率和能量
1、瞬时功率
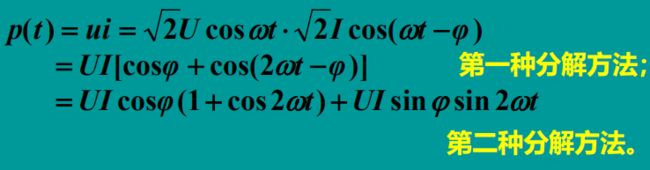
可以看到,其中有一个UIcosϕ,这个也被叫做恒定分量
2、平均功率
上文的恒定分量就是我们的平均功率

ϕ =θu-θi:功率因数角。对无源网络,为其等效阻抗的阻抗角。实际上就是电压领先电流多少角度
cos ϕ :功率因数。
①电阻的平均功率:ϕ =0,故电压与电流同相,P=UI
②电感的平均功率:ϕ =π/2,电压领先,P=0
③电容的平均功率:ϕ =-π/2,电流领先,P=0
平均功率实际上是电阻消耗的功率,亦称为有功功率。表示电路实际消耗的功率,它不仅与电压电流有效值有关,而且与 cosϕ 有关,这是交流和直流的很大区别, 主要由于电压、电流存在相位差
3、无功功率
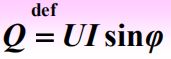
单位:var (乏)
Q>0,表示网络吸收无功功率;
Q<0,表示网络发出无功功率。
Q 的大小反映网络与外电路交换功率的大小。是由储能元件L、C的性质决定的

L与C不断吸收与释放能量,与外部电路不断交换,但未做功