matlab通过切比雪夫实现低通、高通、带通和带阻的设计
椭圆滤波器
设计一个带通椭圆数字滤波器 , 通带为 100 ~200 H z,过渡带均为 50 H z,通带波纹小于 3 db ,阻带衰减为 30 db ,采样频率 f s =1 000 H z 。
fs = 1000;
Rp = 3;Rs = 30;
Wp = 2*[100 200]/fs; % 0-1之间
Ws = 2*[80 220]/fs; % 0-1之间
[n,Wn] = ellipord(Wp,Ws,Rp,Rs); % 确定滤波器的最小阶数n和归一化的低通滤波器截止频率
[b,a] = ellip(n,Rp,Rs,Wn);
巴特沃斯滤波器
fs = 1000; % 信号的采样频率
wp = [8 30]*2/fs; % 通带边界频率 rad/s
ws = [7 32]*2/fs; % 阻带边界频率 rad/s
Rp = 1;% 通带最大波纹 db
Rs = 30;% 阻带最小衰减 db
[N , Wn] = buttord(wp,ws,Rp,Rs); % 阶数和归一化频率Wn
[B , A] = butter(N,Wn);% 得到n阶巴特沃斯滤波器的分子分母
切比雪夫Ⅰ型滤波器的设计
clear;
close all;
clc;
fs = 1000; %Hz 采样频率
Ts = 1/fs;
N = 1000; %序列长度
t = (0:N-1)*Ts;
delta_f = 1*fs/N;
f1 = 50;
f2 = 100;
f3 = 200;
f4 = 400;
x1 = 2*0.5*sin(2*pi*f1*t);
x2 = 2*0.5*sin(2*pi*f2*t);
x3 = 2*0.5*sin(2*pi*f3*t);
x4 = 2*0.5*sin(2*pi*f4*t);
x = x1 + x2 + x3 + x4; %待处理信号由四个分量组成
X = fftshift(abs(fft(x)))/N;
X_angle = fftshift(angle(fft(x)));
f = (-N/2:N/2-1)*delta_f; % 将频率点进行等分处理,好观察堆成的频率
figure(1);
subplot(3,1,1);
plot(t,x);
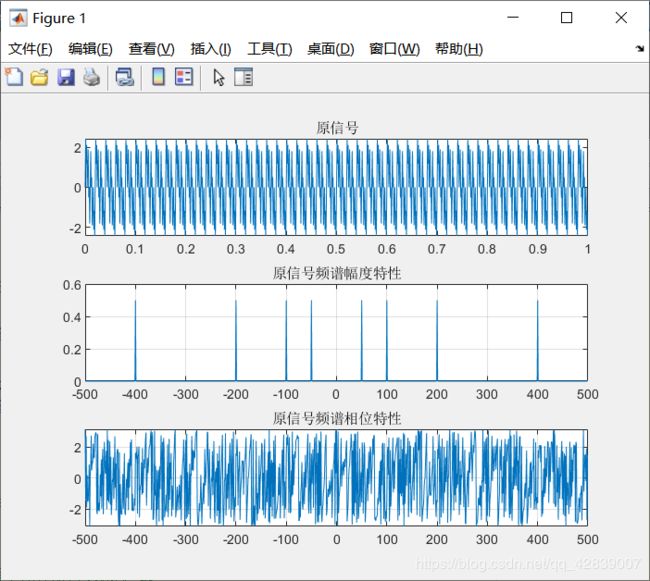
title('原信号');
subplot(3,1,2);
plot(f,X); % 注意这里面要是f的开头为横坐标
grid on;
title('原信号频谱幅度特性');
subplot(3,1,3);
plot(f,X_angle);
title('原信号频谱相位特性');
grid on;
%设计一个切比雪夫低通滤波器,要求把50Hz的频率分量保留,其他分量滤掉
wp = 55/(fs/2); %通带截止频率,取50~100中间的值,并对其归一化
ws = 90/(fs/2); %阻带截止频率,取50~100中间的值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 40;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N1 wc1 ] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = cheby1(N1,alpha_p,wc1,'low');
%滤波
filter_lp_s = filter(b,a,x);
X_lp_s = fftshift(abs(fft(filter_lp_s)))/N;
X_lp_s_angle = fftshift(angle(fft(filter_lp_s)));
figure(2);
freqz(b,a); % 滤波器频谱特性,调用默认区间 0:pi
figure(3);
subplot(3,1,1);
plot(t,filter_lp_s);
grid on;
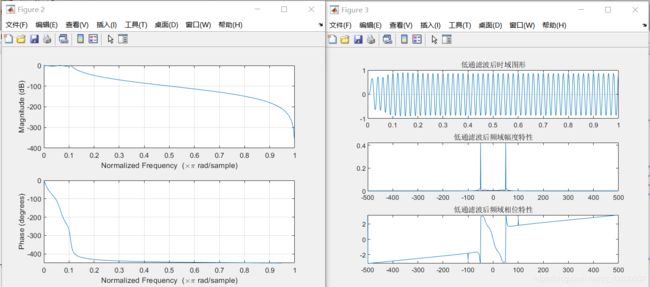
title('低通滤波后时域图形');
subplot(3,1,2);
plot(f,X_lp_s);
title('低通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_lp_s_angle);
title('低通滤波后频域相位特性');
%
%
%设计一个高通滤波器,要求把400Hz的频率分量保留,其他分量滤掉
wp = 350/(fs/2); %通带截止频率,取200~400中间的值,并对其归一化
ws = 380/(fs/2); %阻带截止频率,取200~400中间的值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
% 获取阶数和截止频率
[ N2 wc2 ] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = cheby1(N2,alpha_p,wc2,'high');
%滤波
filter_hp_s = filter(b,a,x);
X_hp_s = fftshift(abs(fft(filter_hp_s)))/N;
X_hp_s_angle = fftshift(angle(fft(filter_hp_s)));
figure(4);
freqz(b,a); %滤波器频谱特性
figure(5);
subplot(3,1,1);
plot(t,filter_hp_s);
grid on;
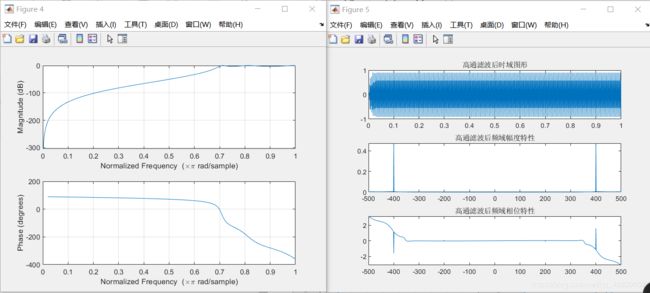
title('高通滤波后时域图形');
subplot(3,1,2);
plot(f,X_hp_s);
title('高通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_hp_s_angle);
title('高通滤波后频域相位特性');
%
%设计一个带通滤波器,要求把50Hz和400Hz的频率分量滤掉,其他分量保留
wp = [65 385 ] / (fs/2); %通带截止频率,50~100、200~400中间各取一个值,并对其归一化
ws = [75 375 ] / (fs/2); %阻带截止频率,50~100、200~400中间各取一个值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N3 wn ] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = cheby1(N3,alpha_p,wn,'bandpass');
%滤波
filter_bp_s = filter(b,a,x);
X_bp_s = fftshift(abs(fft(filter_bp_s)))/N;
X_bp_s_angle = fftshift(angle(fft(filter_bp_s)));
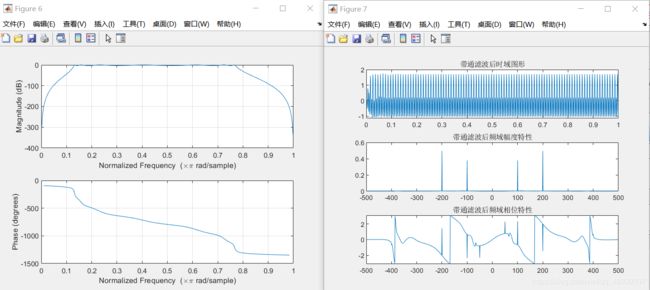
figure(6)
freqz(b,a); %滤波器频谱特性
figure(7);
subplot(3,1,1);
plot(t,filter_bp_s);
grid on;
title('带通滤波后时域图形');
subplot(3,1,2);
plot(f,X_bp_s);
title('带通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_bp_s_angle);
title('带通滤波后频域相位特性');
%
%设计一个带阻滤波器,要求把50Hz和400Hz的频率分量保留,其他分量滤掉
wp = [65 385 ] / (fs/2); %通带截止频率?,50~100、200~400中间各取一个值,并对其归一化
ws = [75 375 ] / (fs/2); %阻带截止频率?,50~100、200~400中间各取一个值,并对其归一
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N4 wn ] = cheb1ord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = cheby1(N4,alpha_p,wn,'stop');
%滤波
filter_bs_s = filter(b,a,x);
X_bs_s = fftshift(abs(fft(filter_bs_s)))/N;
X_bs_s_angle = fftshift(angle(fft(filter_bs_s)));
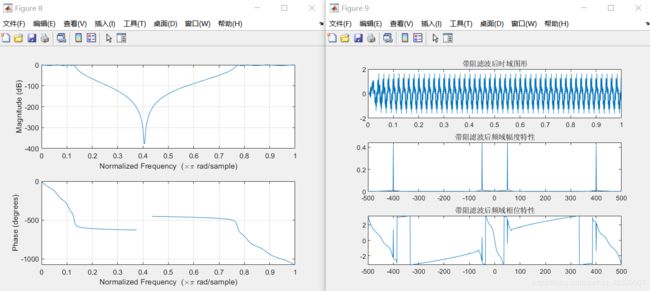
figure(8);
freqz(b,a); %滤波器频谱特性
figure(9);
subplot(3,1,1);
plot(t,filter_bs_s);
grid on;
title('带阻滤波后时域图形');
subplot(3,1,2);
plot(f,X_bs_s);
title('带阻滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_bs_s_angle);
title('带阻滤波后频域相位特性');
原始信号波形
低通滤波
 高通滤波
高通滤波
 带通滤波
带通滤波
 带阻滤波
带阻滤波
转载:https://blog.csdn.net/cqfdcw/article/details/84939698?utm_source=app
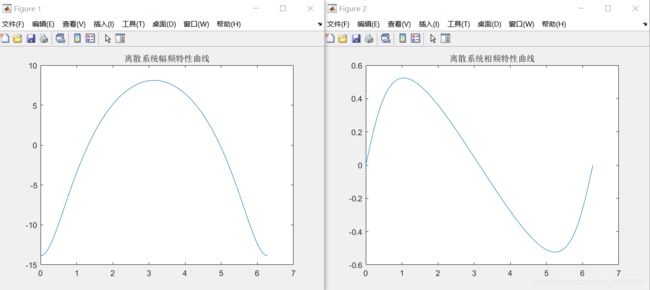
附:求幅频特性曲线和相频特性曲线代码
B=[1 -0.5];
A =[1];
[H,w]=freqz(B,A,[0:2*pi/400:2*pi]);
Hf=abs(H); %取幅度值实部
Hx=angle(H); %取相位值对应相位角
clf;
figure(1);
plot(w,20*log(Hf)); %幅值变换为分贝单位
title('离散系统幅频特性曲线');
figure(2);
plot(w,Hx);
title('离散系统相频特性曲线');
% 或者直接通过下面的代码也是可以得出来的
% B=[1 -0.5];
% A =[1];
% figure;
% freqz(B,A,[0:2*pi/400:2*pi]);