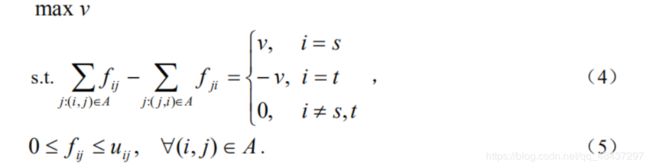第五章 图与网络模型及方法

1 概论

我们首先通过一些例子来了解网络优化问题。
例 1 最短路问题（SPP－shortest path problem）
一名货柜车司机奉命在最短的时间内将一车货物从甲地运往乙地。从甲地到乙地的公路网纵横交错，因此有多种行车路线，这名司机应选择哪条线路呢？假设货柜车的运行速度是恒定的，那么这一问题相当于需要找到一条从甲地到乙地的最短路。
例 2 公路连接问题
某一地区有若干个主要城市，现准备修建高速公路把这些城市连接起来，使得从其中任何一个城市都可以经高速公路直接或间接到达另一个城市。假定已经知道了任意两个城市之间修建高速公路的成本，那么应如何决定在哪些城市间修建高速公路，使得总成本最小？
例 3 指派问题（assignment problem）
一家公司经理准备安排 N 名员工去完成 N 项任务，每人一项。由于各员工的特点不同，不同的员工去完成同一项任务时所获得的回报是不同的。如何分配工作方案可以使总回报最大？
例 4 中国邮递员问题（CPP－chinese postman problem）
一名邮递员负责投递某个街区的邮件。如何为他（她）设计一条最短的投递路线（从邮局出发，经过投递区内每条街道至少一次，最后返回邮局）？由于这一问题是我国管梅谷教授 1960 年首先提出的，所以国际上称之为中国邮递员问题。
例 5 旅行商问题（TSP－traveling salesman problem）
一名推销员准备前往若干城市推销产品。如何为他（她）设计一条最短的旅行路线（从驻地出发，经过每个城市恰好一次，最后返回驻地）？这一问题的研究历史十分悠久，通常称之为旅行商问题。
例 6 运输问题（transportation problem）
某种原材料有 M 个产地，现在需要将原材料从产地运往 N 个使用这些原材料的工厂。假定 M 个产地的产量和 N 家工厂的需要量已知，单位产品从任一产地到任一工厂的运费已知，那么如何安排运输方案可以使总运输成本最低？
上述问题有两个共同的特点：一是它们的目的都是从若干可能的安排或方案中寻求某种意义下的最优安排或方案，数学上把这种问题称为最优化或优化（optimization）问题；二是它们都易于用图形的形式直观地描述和表达，数学上把这种与图相关的结构称为网络（network）。与图和网络相关的最优化问题就是网络最优化或称网络优化（netwok optimization）问题。所以上面例子中介绍的问题都是网络优化问题。由于多数网络优化问题是以网络上的流（flow）为研究的对象，因此网络优化又常常被称为网络流（network flows）或网络流规划等。下面首先简要介绍图与网络的一些基本概念。

2 图与网络的基本概念

2.1 无向图

边上赋权的无向图称为赋权无向图或无向网络（undirected network）。我们对图和网络不作严格区分，因为任何图总是可以赋权的。
一个图称为有限图，如果它的顶点集和边集都有限。图G 的顶点数用符号|V | 或 ν (G) 表示，边数用| E |或ε (G)表示。
当讨论的图只有一个时，总是用G 来表示这个图。从而在图论符号中我们常略去字母G ，例如，分别用V,E,ν 和ε 代替V (G),E(G),ν (G) 和ε (G)。
端点重合为一点的边称为环(loop)。
一个图称为简单图(simple graph)，如果它既没有环也没有两条边连接同一对顶点。

2.2 有向图

对应于每个有向图 D ，可以在相同顶点集上作一个图G ，使得对于 D 的每条弧，G 有一条有相同端点的边与之相对应。这个图称为 D 的基础图。反之，给定任意图G ，对于它的每个边，给其端点指定一个顺序，从而确定一条弧，由此得到一个有向图，这样的有向图称为G 的一个定向图。
以下若未指明“有向图”三字，“图”字皆指无向图。

2.3 完全图、二分图

	每一对不同的顶点都有一条边相连的简单图称为完全图(complete graph)。n 个顶点的完全图记为 Kn 。 若V (G) = X UY ， X 交Y = Φ ，| X ||Y |≠ 0（这里| X |表示集合 X 中的元素个数）， X 中无相邻顶点对，Y 中亦然，则称G 为二分图(bipartite graph)；特别地，若∀x ∈ X,∀y ∈Y ，则 xy ∈ E(G)，则称G 为完全二分图，记成 K_{|X|,|Y|} 。

2.4 子图

	 图H 叫做图 G 的子图（subgraph），记作 H ⊂ G ，如果 V (H ) ⊂V (G) ， E(H) ⊂ E(G) 。若 H 是G 的子图，则G 称为 H 的母图。 
	 G 的支撑子图（spanning subgraph，又成生成子图）是指满足V(H) =V(G) 的子图 H 。

2.5 顶点的度

	设v ∈V (G) ，G 中与v 关联的边数（每个环算作两条边）称为v 的度(degree)，记作d(v)。若d(v)是奇数，称v 是奇顶点(odd point)；d(v)是偶数，称v 是偶顶点(even point)。关于顶点的度，我们有如下结果：
	(i)\begin{equation*} \sum_{v ∈V}d(v)\end{equation*} = 2ε
	(ii) 任意一个图的奇顶点的个数是偶数

2.6 图与网络的数据结构

	这里我们介绍计算机上用来描述图与网络的 5 种常用表示方法：邻接矩阵表示法、关联矩阵表示法、弧表表示法、邻接表表示法和星形表示法。

2.7 轨与连通

	W= v_0 e_1 v_1 e_2…e_k v_k  ，其中e_i ∈E(G) ，1 ≤ i ≤ k ，v_j  ∈ V (G)  ，0 ≤ j ≤ k ，  e_i 与v_{i-1} ,v_i 关联，称W 是图G 的一条道路(walk)，k 为路长，顶点  v_0 和  v_k 分别称为W 的起点和终点，而 v_1 , v_2, …， v_{k-1} 称为它的内部顶点。
	若道路W 的边互不相同，则W 称为迹(trail)。若道路W 的顶点互不相同，则W 称为轨(path)。
	称一条道路是闭的，如果它有正的长且起点和终点相同。起点和终点重合的轨叫做圈(cycle)。
	若图G 的两个顶点u, v 间存在道路，则称u 和v 连通(connected)。u, v 间的最短轨的长叫做u, v 间的距离。记作d(u,v) 。若图G 的任二顶点均连通，则称G 是连通图。显然有：
	(i) 图 P 是一条轨的充要条件是 P 是连通的，且有两个一度的顶点，其余顶点的度为 2；
	(ii) 图C 是一个圈的充要条件是C 是各顶点的度均为 2 的连通图.

3 应用—最短路问题

3.1 两个指定顶点之间的最短路径

	求最短路已有成熟的算法：迪克斯特拉（Dijkstra）算法，其基本思想是按距u_0 从近到远为顺序，依次求得u_0 到G 的各顶点的最短路和距离，直至 v_0 （或直至G 的所有顶点），算法结束。为避免重复并保留每一步的计算信息，采用了标号算法。
	例 9 某公司在六个城市  c_1 , c_2 ,…, c_6 中有分公司，从  c_i 到  c_j 的直接航程票价记在下述矩阵的(i, j) 位置上。（∞表示无直接航路），请帮助该公司设计一张城市  c_1 到其它城市间的票价最便宜的路线图。

求第一个城市到其它城市的最短路径的 Matlab 程序如下：
clc,clear
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a’;
a(find(a0))=inf;
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));
d(1:length(a))=inf;d(1)=0;temp=1;
while sum(pb) tb=find(pb0);
d(tb)=min(d(tb),d(temp)+a(temp,tb));
tmpb=find(d(tb)==min(d(tb)));
temp=tb(tmpb(1));
pb(temp)=1;
index1=[index1,temp];
temp2=find(d(index1)==d(temp)-a(temp,index1));
index2(temp)=index1(temp2(1));
end
d, index1, index2
运行得：
d =
0 35 45 35 25 10
index1 =
1 6 5 2 4 3
index2 =
1 6 5 6 1 1

3.2 两个指定顶点之间最短路问题的数学表达式

3.3 每对顶点之间的最短路径

	计算赋权图中各对顶点之间最短路径，显然可以调用 Dijkstra 算法。具体方法是：每次以不同的顶点作为起点，用 Dijkstra 算法求出从该起点到其余顶点的最短路径，反复执行 n −1次这样的操作，就可得到从每一个顶点到其它顶点的最短路径。这种算法的时间复杂度为  O(n^3) 。第二种解决这一问题的方法是由 Floyd R W 提出的算法，称之为 Floyd 算法。
	例12 用Floyd算法求解例9。

矩阵path用来存放每对顶点之间最短路径上所经过的顶点的序号。Floyd算法的Matlab程序如下：
clear;clc;
n=6; a=zeros(n);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25; a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25; a(5,6)=55;
a=a+a’; M=max(max(a))*n^2; %M为充分大的正实数
a=a+((a==0)-eye(n))*M;
path=zeros(n);
for k=1:n
for i=1:n
for j=1:n
if a(i,j)>a(i,k)+a(k,j)
a(i,j)=a(i,k)+a(k,j);
path(i,j)=k;
end
end
end
end
a, path

我们使用LINGO9.0编写的FLOYD算法如下：
model:
sets:
nodes/c1…c6/;
link(nodes,nodes):w,path; !path标志最短路径上走过的顶点;
endsets
data:
path=0;
w=0;
@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):
@format(w(i,j),’ 10.0f’)),@newline(1));
@text(mydata1.txt)=@write(@newline(1));
@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):
@format(path(i,j),’ 10.0f’)),@newline(1));
enddata
calc:
w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;
w(2,3)=15;w(2,4)=20;w(2,6)=25;
w(3,4)=10;w(3,5)=20;
w(4,5)=10;w(4,6)=25;w(5,6)=55;
@for(link(i,j):w(i,j)=w(i,j)+w(j,i));
@for(link(i,j) |i#ne#j:w(i,j)=@if(w(i,j)#eq#0,10000,w(i,j)));
@for(nodes(k):@for(nodes(i):@for(nodes(j):
tm=@smin(w(i,j),w(i,k)+w(k,j));
path(i,j)=@if(w(i,j)#gt# tm,k,path(i,j));w(i,j)=tm)));
endcalc
end

4 树

4.1 基本概念

4.2 应用—连线问题

例 13 用 prim 算法求图 5 的最小生成树。
我们用 result_{3xn}的第一、二、三行分别表示生成树边的起点、终点、权集合。Matlab程序如下：
clc;clear;
a=zeros(7);
a(1,2)=50; a(1,3)=60;
a(2,4)=65; a(2,5)=40;
a(3,4)=52;a(3,7)=45;
a(4,5)=50; a(4,6)=30;a(4,7)=42;
a(5,6)=70;
a=a+a’;a(find(a==0))=inf;
result=[];p=1;tb=2:length(a);
while length(result)~=length(a)-1
temp=a(p,tb);temp=temp(;
d=min(temp);
[jb,kb]=find(a(p,tb)d);
j=p(jb(1));k=tb(kb(1));
result=[result,[j;k;d]];p=[p,k];tb(find(tbk))=[];
end
result
运行结果：
result =
1 2 5 4 4 7
2 5 4 6 7 3
50 40 50 30 42 45

4.2.1 Kruskal 算法构造最小生成树

例 14 用 Kruskal 算法构造图5 的最小生成树。
Matlab 程序如下：
clc;clear;
a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40;
a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;
a(4,7)=42; a(5,6)=70;
[i,j,b]=find(a);
data=[i’;j’;b’];index=data(1:2,:);
loop=max(size(a))-1;
result=[];
while length(result) temp=min(data(3,:));
flag=find(data(3,:)temp);
flag=flag(1);
v1=index(1,flag);v2=index(2,flag);
if v1~=v2
result=[result,data(:,flag)];
end
index(find(indexv2))=v1;
data(:,flag)=[];
index(:,flag)=[];
end
result
运行结果如下：
result =
4 2 4 3 1 4
6 5 7 7 2 5
30 40 42 45 50 50

5 匹配问题

	定义 若 M ⊂ E(G) ，∀e_i ,e_j ∈ M ， e_i 与 e_j 无公共端点（i ≠ j ），则称 M 为图G 中的一个对集；M 中的一条边的两个端点叫做在对集 M 中相配；M 中的端点称为被 M 许配；G 中每个顶点皆被 M 许配时，M 称为完美对集；G 中已无使| M '|>| M |的对集 M ' ，则 M 称为最大对集；若G 中有一轨，其边交替地在对集 M 内外出现，则称此轨为 M 的交错轨，交错轨的起止顶点都未被许配时，此交错轨称为可增广轨。若把可增广轨上在 M 外的边纳入对集，把 M 内的边从对集中删除，则被许配的顶点数增加 2，对集中的“对儿”增加一个。
	1957 年，贝尔热(Berge)得到最大对集的充要条件：
	定理 2 M 是图G 中的最大对集当且仅当G 中无 M 可增广轨。
	1935 年，霍尔(Hall)得到下面的许配定理：
	定理 3 G 为二分图， X 与Y 是顶点集的划分，G 中存在把 X 中顶点皆许配的对集的充要条件是，∀S ⊂ X ，则| N(S) |≥| S |，其中 N(S) 是 S 中顶点的邻集。
	由上述定理可以得出：
	推论 1：若G 是k 次（k > 0) 正则 2 分图，则G 有完美对集。
	所谓k 次正则图，即每顶点皆k 度的图。
	由此推论得出下面的婚配定理：
	定理 4 每个姑娘都结识k(k ≥ 1) 位小伙子，每个小伙子都结识k 位姑娘，则每位姑娘都能和她认识的一个小伙子结婚，并且每位小伙子也能和他认识的一个姑娘结婚。
	人员分派问题等实际问题可以化成对集来解决。
	人员分派问题：工作人员 x_1,x_2,…,x_n去做n 件工作 y_1,y_2,…,y_n，每人适合做其中一件或几件，问能否每人都有一份适合的工作？如果不能，最多几人可以有适合的工作？
	这个问题的数学模型是： G 是二分图，顶点集划分为 V (G) = X UY ，X =  { x_1,… ,x_n } , Y = {y_1, …,y_n} ，当且仅当 x_i 适合做工作 y_j 时，x_i y_j ∈E(G) ∈，求G 中的最大对集。
	解决这个问题可以利用 1965 年埃德门兹(Edmonds)提出的匈牙利算法

6 Euler 图和 Hamilton 图

6.1 基本概念

	定义 经过G 的每条边的迹叫做G 的 Euler 迹；闭的 Euler 迹叫做 Euler 回路或 E回路；含 Euler 回路的图叫做 Euler 图。直观地讲，Euler 图就是从一顶点出发每边恰通过一次能回到出发点的那种图，即不重复地行遍所有的边再回到出发点。
	定理 6 （i）G 是 Euler 图的充分必要条件是G 连通且每顶点皆偶次。
	（ ii ） G 是 Euler 图的充分必要条件是 G 连通且 XXXXX， C_i 是圈，XXXXXX 。 (插入图片出问题）
	（iii）G 中有 Euler 迹的充要条件是G 连通且至多有两个奇次点。
	定义 包含G 的每个顶点的轨叫做 Hamilton(哈密顿)轨；闭的 Hamilton 轨叫做Hamilton 圈或 H 圈；含 Hamilton 圈的图叫做 Hamilton 图。
	直观地讲，Hamilton 图就是从一顶点出发每顶点恰通过一次能回到出发点的那种图，即不重复地行遍所有的顶点再回到出发点。

6.2 Euler 回路的 Fleury 算法

	1921 年，Fleury 给出下面的求 Euler 回路的算法。
	Fleury 算法：
1 .   ∀v_0 ∈V (G) ，令 W_0 = v_0 。

2 . 假设迹 W_i = v_0 e_1 v_1…e_i v_i 已经选定，那么按下述方法从 E - {e_1 ,… ,e_i } 中选取边 e_{i+1} ：
（i） e_{i+1} 和 v_i 相关联；
（ii）除非没有别的边可选择，否则 e_{i+1} 不是 G_i = G - {e_1,…,e_i} 的割边(cut edge)。 (所谓割边是一条删除后使连通图不再连通的边)。
3 . 当第 2 步不能再执行时，算法停止。

7 最大流问题

7.1 最大流问题的数学描述

7.1.1 网络中的流

定义 在以V 为节点集， A 为弧集的有向图G = (V, A) 上定义如下的权函数：
（i） L : A → R 为孤上的权函数，弧 (i, j)∈ A 对应的权 L(i, j) 记为 l_ij ，称为孤
(i, j) 的容量下界（lower bound）； （ii）U : A → R 为弧上的权函数，弧(i, j)∈ A对应的权U(i, j) 记为u_ij ，称为孤
(i, j) 的容量上界，或直接称为容量（capacity）； （iii） D :V → R 为顶点上的权函数，节点i ∈V 对应的权 D(i) 记为 d_i ，称为顶点i 的供需量（supply／demand）；
此时所构成的网络称为流网络，可以记为
N = (V, A,L,U,D) 。
由于我们只讨论V, A 为有限集合的情况，所以对于弧上的权函数 L,U 和顶点上的权函数 D ，可以直接用所有孤上对应的权和顶点上的权组成的有限维向量表示，因此L,U, D 有时直接称为权向量，或简称权。由于给定有向图G = (V, A) 后，我们总是可以在它的弧集合和顶点集合上定义各种权函数，所以流网络一般也直接简称为网络。
在流网络中，弧(i, j) 的容量下界 l_ij 和容量上界u_ij 表示的物理意义分别是：通过该弧发送某种“物质”时，必须发送的最小数量为 l_ij ，而发送的最大数量为u_ij 。顶点i ∈V对应的供需量d_i 则表示该顶点从网络外部获得的“物质”数量（d_i > 0时），或从该顶点发送到网络外部的“物质”数量（d_i < 0 时）。下面我们给出严格定义。

则称 f 为可行流（feasible flow）。至少存在一个可行流的流网络称为可行网络（feasible network）．约束（1）称为流量守恒条件（也称流量平衡条件），约束（2）称为容量约束。
可见，当d_i > 0时，表示有d_i 个单位的流量从网络外部流入该顶点，因此顶点i 称为供应点（supply node）或源（source），有时也形象地称为起始点或发点等；当d_i < 0时，表示有|d_i | 个单位的流量从该顶点流失到网络外部（或说被该顶点吸收），因此顶点i 称为需求点（demand node）或汇（sink），有时也形象地称为终止点或收点等；当d_i = 0时，顶点i 称为转运点（transshipment node）或平衡点、中间点等。此外，根据（1）可知，对于可行网络，必有

也就是说，所有节点上的供需量之和为 0 是网络中存在可行流的必要条件。 一般来说，我们总是可以把 L ≠ 0 的流网络转化为 L = 0 的流网络进行研究。所以，除非特别说明，以后我们总是假设 L = 0 （即所有孤 (i, j) 的容量下界 lij = 0 ），并将L = 0 时的流网络简记为 N = (V, A,U,D)。此时，相应的容量约束（2）为 0 ≤ f_ij ≤ u_ij , ∀(i, j) ∈ A 。
定义 在流网络 N = (V, A,U,D)中，对于流 f ，如果
f_ij = 0, ∀(i, j)∈ A，则称 f 为零流，否则为非零流。如果某条弧(i, j) 上的流量等于其容量（ f_ij =u_ij ），则称该弧为饱和弧（saturated arc）；如果某条弧(i, j) 上的流量小于其容量（ f_ij

7.1.2 最大流问题

	考虑如下流网络 N = (V, A,U,D)：节点 s 为网络中唯一的源点，t 为唯一的汇点，而其它节点为转运点。如果网络中存在可行流 f ，此时称流 f 的流量（或流值，flow value）为d_s （根据（3），它自然也等于 − d_t ），通常记为v 或v( f ) ，即

v = v( f ) = d_s= −d_t 。
对这种单源单汇的网络，如果我们并不给定 d_s 和 d_t （即流量不给定），则网络一般记为 N = (s,t,V, A,U) 。最大流问题（ maximum flow problem ）就是在N = (s,t,V, A,U) 中找到流值最大的可行流（即最大流）。我们将会看到，最大流问题的许多算法也可以用来求解流量给定的网络中的可行流。也就是说，当我们解决了最大流问题以后，对于在流量给定的网络中寻找可行流的问题，通常也就可以解决了。
因此，用线性规划的方法，最大流问题可以形式地描述如下：