实验四 用窗函数法设计FIR数字滤波器

实验目的：

1、熟悉线性相位FIR滤波器的幅频特性和相频特性；
2、加深对窗函数法设计FIR数字滤波器的基本原理的理解；
3、了解Matlab有关窗函数法设计的子函数以及各种不同窗函数对滤波器性能的影响。
实验原理：

根据上式中的正、负号和长度N取为奇数
或偶数又将线性相位FIR滤波器分成四类。 要 根据所设计的滤波特性正确选择其中一类。

对于理想的数字低通滤波器频率响应，有下列子程序实现（程序名为ideallp.m）：

function hd=ideallp(wc,N)
tao=(N-1)/2;
n=[0:(N-1)];
m=n-tao+eps;
hd=sin(wc*m)./(pi*m);

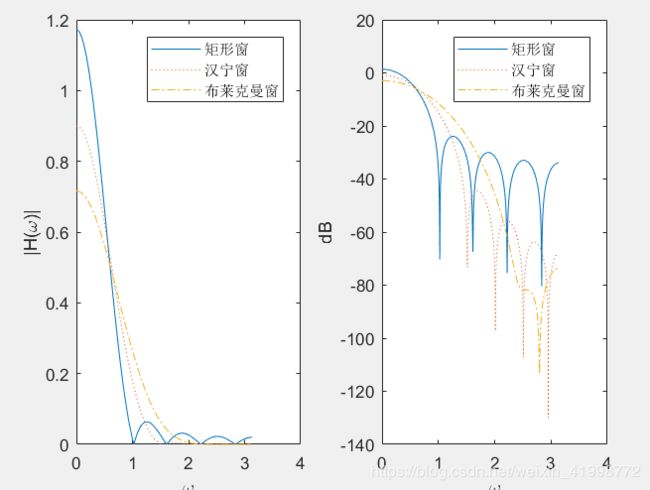
实例：已知某FIR数字低通滤波器截止频率wc=0.2π，滤波器长度N=11，分别用矩形窗、汉 宁窗和布莱克曼窗来设计该滤波器，绘制幅频响应曲线和损耗函数曲线。

wc=0.2*pi; N=11;
hd= ideallp(wc,N); % 用wc=0.2*pi的理想低通作为逼近滤波器
wd1=boxcar(N)' ; b1=hd.*wd1; % 用矩形窗设计：
wd2=hanning(N)'; b2=hd.*wd2; % 用汉宁窗设计：
wd3=blackman(N)' ;b3=hd.*wd3; % 用布莱克曼窗设计：
[H1,w]=freqz(b1,1); % 用矩形窗设计的频率特性
[H2,w]=freqz(b2,1); % 用汉宁窗设计的频率特性
[H3,w]=freqz(b3,1); % 用布莱克曼窗设计的频率特性
subplot(1,2,1), plot(w,abs(H1),w,abs(H2),':',w,abs(H3),'-.');% 绘幅特性
legend('矩形窗','汉宁窗','布莱克曼窗')
xlabel('\omega'),ylabel('|H(\omega)|')
subplot(1,2,2), % 绘分贝幅特性
plot(w,20*log10(abs(H1)),w,20*log10(abs(H2)),':',w,20*log10(abs(H3)),'-.');
legend('矩形窗','汉宁窗','布莱克曼窗')
xlabel('\omega'),ylabel('dB')

————————————————
freqz（）函数
MATLAB提供了专门用于求离散系统频响特性的函数freqz()，调用freqz()的格式有以下几种：

(1)[H,w]=freqz(B,A,N); %N默认值为512

(2)[H,w]=freqz(B,A,N,‘whole’);

(3)[H,w]=freqz(B,A,[自定义区间]);

上式中B和A分别对应离散系统的系统函数H(z)的分子、分母多项式的系数向量：

   B=[b1,b2,...];    A=[a1,a2,...];

返回量H则包含了离散系统对应区间内N（N为正整数）个频率等分点的频率响应，w为N个频率等分点的值。

(1)式调用默认区间 0：pi

(2)式调用主值区间 -pi：pi

(3)式自定义区间，如[0:2pi/n:2pi]

最后利用abs()和angle()函数及plot()函数，即可绘制出系统在频率区间的频响曲线。

————————————————

原文链接：https://blog.csdn.net/machinelearning_er/article/details/79444352