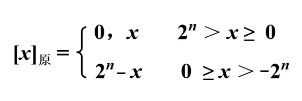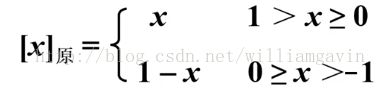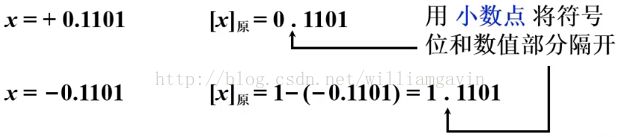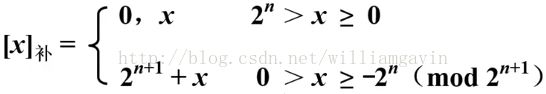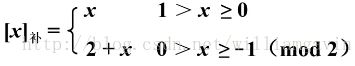无符号数和有符号数（一） -- 原码表示法和补码表示法

无符号数：

即没有符号的数。 在c语言中就是 unsigned 类型的。 无符号数在计算机中的存储较为简单， 因为没有符号位， 直接将数字化成二进制然后存储在对应的存储器或者寄存器中。 这时寄存器或者存储器的位数就可以表示数值的范围， 比如：如果是 8 位的， 表示的范围为 0 ~ 255。

有符号数：

即有符号的数， 符号数存储时不仅要将数据部分存入计算机， 还要将符号数字化的存进去。

1， 机器数和真值

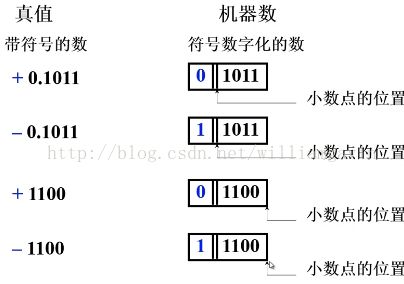
机器数就是在计算机里面存储的数， 真值是带符号的数。

在以上数据的表示中， 一共需要解决三个问题：第一是符号位的表示； 第二是数值部分的表示； 第三是小数点位置的表示。

注意：在计算机里面没有专门的硬件是用来表示小数的， 小数都是以约定的形式给出的， 比如放在符号位的后面； 符号位也是如此， 比如约定用最高位来表示符号位。 根据这种方式可以将定点计算机（小数点固定的计算机）分为整数定点机（小数点在最后面）和小数定点机（小数点在符号位后面）。实际上将符号位数值化这种表示方式就是原码表示法。

二， 原码表示法

1， 整数

n 为数值位的位数， x 是真值。 当 2^n >= x >= 0; 时， 符号位为 0（0 表示正， 1 表示负）。当 0 >= x >= -2^n 时， 最高位

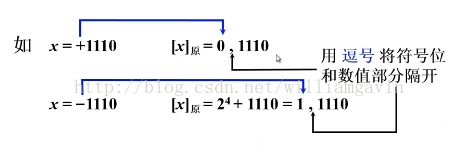
为 1， 因为数值位一共 n 位， 加上符号位一共 n+1 位， 所以 2^n 表示最高位为 1。 比如：

原码表示法就是带符号的绝对值表示。 从上面的原码表示形式来看， 整数 0 有两种不同的表示方法。

2， 小数

x 为真值。下面是两个小数的具体例子

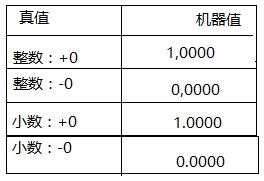
注意无论是整数的 “，” 还是小数的“ . ” 在计算机里面都是不存储的， 都是约定形成的。 还是小数 0 也有两种不同的表示方式。

也就是说， 在原码表示法里面， 0 有四种不同的表示方式

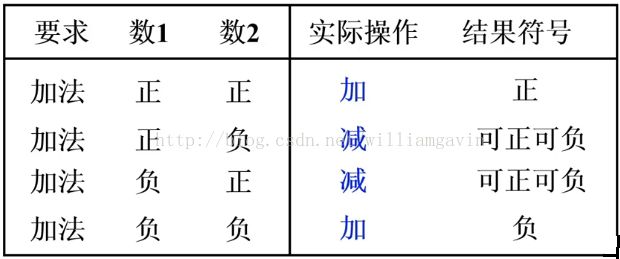
原码的特点是简单直观。 但是原码做加法操作时会出现以下问题：

也就是说， 对于两个异号的数相加实际上还是进行减法操作， 这对运算器来说就比较麻烦， 能不能将减法转换成加法？

这个用补码可以解决。

三、补码表示法

（1）首先弄清楚“补”的概念。 在一块能显示0 ~ 12 的时钟上面， 如果现在是 6 点， 现在想要调到 2 点， 有两种方式； 第一种向后面拨 4 个小时，

第二种向前面拨八个小时； 也就是 6 - 4 = 6 + 8， 在模为 12 的情况下； 我们称 -4 是 8 以 12 位模的补数。如此可以将减法转化成加法。 可以得到

以下结论：

一：一个负数加上“模”得到该负数的补数。

二：一个正数和一个负数互为补数时 ，它们绝对值的和为 “模”。

在计数器中， 模为 16. 如果我们需要将 1011 变成 0000 ， 怎么变换呢？ 模为 16

第一种方式：1011 - 1011 = 0000

第二种方式：1011 + 0101 = 1 0000； 但是因为是在4 位寄存器里面进行的， 所以高位 1 自动去除。

如果是负数呢？ 比如 -0.1001变成 0.0000呢？， 在模为 2 的情况下

第一种方式： -0.1001 - (-0.1001) = 0.0000

第二种方式：-0.1001 + 1.0111 = 10.0000; 高位自动去除

（2）正数的补数为它本身

-1011 = + 0101 (mod 16); 在模为 16 的时候 - 1011 的补数为 + 0101， 将这两个数同时加上 “模”， -1011的模为 + 0101， + 0101加上模之后它的

补数还是+ 0101（最高位会扔掉）， 也就是说 - 1011和 + 0101 的补数都是 + 0101。 那么+ 0101 到底是 -1011 还是 + 0101的补数呢？ 可以用符号位

来加以区分：+ 0101 的 补数是 0,0101（0 表示正）； - 1011的补数是 1,0101（1 表示 负）。

那么这种方法是怎么实现的呢？

实际上是将模 改成 2^5 。这样 - 1011 + 100000 = 1,0101（符号位与数值位之间用逗号隔开）。 + 0101 + 100000 = 10,0101（最高位去除）

（3）补码定义：

整数

x 为真值， 前面的 0 是符号位。n 为位数； 注意 模 为 n + 1。

举例：

x = + 1011， 它的补码为：0，1011。

x = - 1011000， 首先确定 n 等于 7， 所以 模 为2^8, 补码为： 100000000 - 1011000 = 1，0101000

小数：

x 表示真值。

举例：

x = 0.1110 补码为：0.1110, 最高位表示符号位。

x = - 0.1100000 补码为：1.0100000, 最高位同样表示符号位

注意上面的 mod 2 （模为 2）并不是确定的。可以为 mod 4 （模为 4）， mod 8（模 为 8）； 但是如果不是mod 2 的话， 符号位也会变化。

从前面的求法可以看出， 负数的补码求法略显麻烦， 因为每次都要进行减法运算； 下面介绍一种比较方便的方法：

（4）求补码的快捷方式

设 x = - 1010， 我们可以经过如下步骤得到 x 的补码：

注意：此时的补码为：1,0110； 原码为：1,1010（负号用 1 表示）。 所以可以得到 补码 = ! 原码 + 1。

负数的补码等于原码的数值位取反加 1。 同样 负数的原码也是符号位不变， 补码数值位取反加 1 。原码 = ！补码 + 1.

这个比用公式快得多。

结论：补码表示法中， 正数的补码等于原码本身； 负数的补码等于原码数值位取反加 1。 原码变补码和补码变原码的方法是一样的。