【力扣周赛】第184 场 | 5380,5381，5382，5383

5380 数组中的字符串匹配

给你一个字符串数组 words ，数组中的每个字符串都可以看作是一个单词。请你按 任意 顺序返回 words 中是其他单词的子字符串的所有单词。

如果你可以删除 words[j] 最左侧和/或最右侧的若干字符得到 word[i] ，那么字符串 words[i] 就是 words[j] 的一个子字符串。

翻译：输出words中可以作为words内元素子字符串的元素。

算法

class Solution(object):
    def stringMatching(self, words):
        """
        :type words: List[str]
        :rtype: List[str]
        """
        words.sort(key=len,reverse=True)
        k,res=[],[]
        for i in words:
            if not k:k.append(i)
            elif k:
                for j in k:
                    if i in j:
                        res.append(i)
                        break
                k.append(i)
        return res

5381 查询带键的排列

给你一个待查数组 queries ，数组中的元素为 1 到 m 之间的正整数。 请你根据以下规则处理所有待查项 queries[i]（从 i=0 到 i=queries.length-1）：

一开始，排列 P=[1,2,3,…,m]。
对于当前的 i ，请你找出待查项 queries[i] 在排列 P 中的位置（下标从 0 开始），然后将其从原位置移动到排列 P 的起始位置（即下标为 0 处）。注意， queries[i] 在 P 中的位置就是 queries[i] 的查询结果。
请你以数组形式返回待查数组 queries 的查询结果。

示例 1：
输入：queries = [3,1,2,1], m = 5
输出：[2,1,2,1]
解释：待查数组 queries 处理如下：
对于 i=0: queries[i]=3, P=[1,2,3,4,5], 3 在 P 中的位置是 2，接着我们把 3 移动到 P 的起始位置，得到 P=[3,1,2,4,5] 。
对于 i=1: queries[i]=1, P=[3,1,2,4,5], 1 在 P 中的位置是 1，接着我们把 1 移动到 P 的起始位置，得到 P=[1,3,2,4,5] 。
对于 i=2: queries[i]=2, P=[1,3,2,4,5], 2 在 P 中的位置是 2，接着我们把 2 移动到 P 的起始位置，得到 P=[2,1,3,4,5] 。
对于 i=3: queries[i]=1, P=[2,1,3,4,5], 1 在 P 中的位置是 1，接着我们把 1 移动到 P 的起始位置，得到 P=[1,2,3,4,5] 。
因此，返回的结果数组为 [2,1,2,1] 。

完全根据示例1写算法

算法

class Solution(object):
    def processQueries(self, queries, m):
        """
        :type queries: List[int]
        :type m: int
        :rtype: List[int]
        """
        P=list(range(1,m+1))
        res=[]
        for i in queries:
            idx=P.index(i)
            res.append(idx)
            P.insert(0,P.pop(idx))
        return res

5382 HTML 实体解析器

「HTML 实体解析器」 是一种特殊的解析器，它将 HTML 代码作为输入，并用字符本身替换掉所有这些特殊的字符实体。

HTML 里这些特殊字符和它们对应的字符实体包括：

双引号：字符实体为 " ，对应的字符是 " 。
单引号：字符实体为 ’ ，对应的字符是 ’ 。
与符号：字符实体为 & ，对应对的字符是 & 。
大于号：字符实体为 > ，对应的字符是 > 。
小于号：字符实体为 < ，对应的字符是 < 。
斜线号：字符实体为 ⁄ ，对应的字符是 / 。
给你输入字符串 text ，请你实现一个 HTML 实体解析器，返回解析器解析后的结果。

算法

class Solution(object):
    def entityParser(self, text):
        """
        :type text: str
        :rtype: str
        """
        for i,j in [['"','"'],[''',"'"],['>','>'],['<','<'],['⁄','/'],['&','&']]:
            text=text.replace(i,j)
        return text

这里有一点就是字符串的方法一般都返回副本，而不是修改原字符串。

5383 给 N x 3 网格图涂色的方案数

你有一个 n x 3 的网格图 grid ，你需要用 红，黄，绿 三种颜色之一给每一个格子上色，且确保相邻格子颜色不同（也就是有相同水平边或者垂直边的格子颜色不同）。

给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大，请你返回答案对 10^9 + 7 取余的结果。

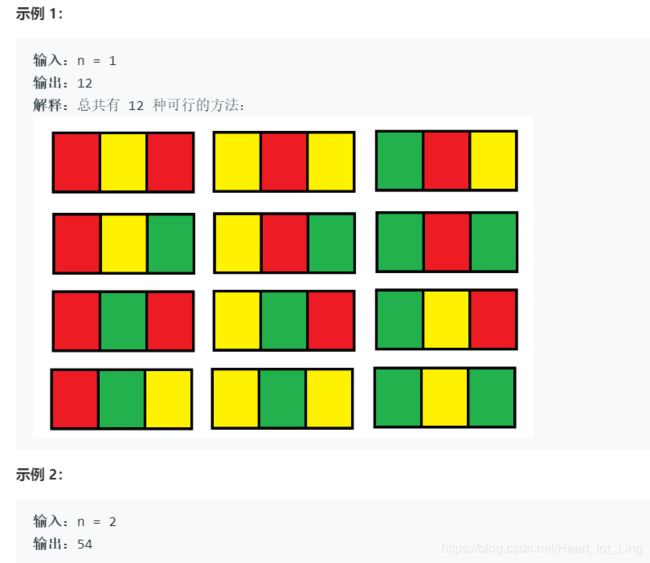
吐了，先是用回溯做了这道题，写完后看到n=5000我陷入了沉思……
我居然第一时间萌生了修改递归栈的深度……
然后醒悟这是道数学规律题……

input:1–out:12
input:2–out:54 6*(4+5)
input:3–out:246 6*(5*5+4*4)
……
……
……
我好恨/嘤嘤嘤，最后时间不够，没时间去好好思考规律所在。

在第一层可以摆出6个ABA类型的和6个ABC类型的涂法。对于下面每一层，每一个ABA涂法可以拼接2个ABC涂法和3个ABA涂法，每一个ABC涂法可以拼接2个ABC涂法和2个ABA涂法。这样迭代可以算出第N层有几种ABA涂法和ABC涂法，相加就是答案。

class Solution:
    def numOfWays(self, n):
        x, y = 6, 6
        for _ in range(n - 1):
            X, Y = x, y
            x = X * 3 + Y * 2
            y = X * 2 + y * 2
        return (x + y) % 1000000007

气死ing。

保存一个周赛时写的回溯算法

class Solution(object):
    def numOfWays(self, n):
        tp=[[None for i in range(3)]for j in range(n)]
        color=['red','yellow','green']
        res=0
        cc=set()
        def x(i,j):
            j += 1
            if j == 3:
                i += 1
                j = 0
            return i,j
        def rex(i,j):
            if j==0:
                i-=1
                j=2
            else:
                j-=1
            return i,j
        def h(n,i=0,j=0):
            nonlocal res
            if i==n and j==0:
                res+=1
                print(tp)
                return
            for k in color:
                if i == 0:
                    if j == 0 or 0 <= j - 1 < 3 and tp[i][j - 1] != k:
                        tp[i][j] = k
                        i,j=x(i,j)
                        h(n,i,j)
                        i,j=rex(i,j)
                elif j == 0:
                    if i == 0 or 0 <= i - 1 < n and tp[i - 1][j] != k:
                        tp[i][j] = k
                        i,j=x(i,j)
                        h(n,i,j)
                        i, j = rex(i, j)
                else:
                    if 0 <= i - 1 < n and tp[i-1][j] != k and 0 <= j - 1 < 3 and tp[i][j - 1] != k:
                        tp[i][j] = k
                        i,j=x(i,j)
                        h(n,i,j)
                        i, j = rex(i, j)
        h(n)
        return res