vijos-p1143 2008.11.9

vijos-p1143 2008.11.9

动态规划  vijos-p1143三取方格数+二取方格数 Hascomments

小结：不管是几取方格数都可以这样考虑：n取方格数

1．    抽象成n个人从左上角到右下角，而且(1,1)(n,n)的格子上的数是必须取的

2．   有两种划分阶段的方法：

（1） 把n个人的横纵坐标都算在状态表示之内。

F[x1,y1,x2,y2,….xn,yn]适用于n<=2时

（2） 以走了k步时，n个人的横坐标来表示状态（纵坐标可以由k,和横坐标推出）注意，x1,x2,x3…的循环终值是当前要走第几步

f[k,x1,x2,…xn]，适用于n很大时

3．心得：能减少的状态就尽量减少

三取方格数

背景 Background 

JerryZhou同学经常改编习题给自己做。

这天，他又改编了一题。。。。。

描述 Description  

设有N*N的方格图，我们将其中的某些方格填入正整数，

而其他的方格中放入0。

某人从图得左上角出发，可以向下走，也可以向右走，直到到达右下角。

在走过的路上，他取走了方格中的数。（取走后方格中数字变为0）

此人从左上角到右下角共走3次，试找出3条路径，使得取得的数总和最大。

输入格式 Input Format 

第一行:N   (4<=N<=20)

接下来一个N*N的矩阵，矩阵中每个元素不超过80，不小于0 

输出格式 Output Format 

一行，表示最大的总和。

样例输入 Sample Input  

4

12 3 4

21 3 4

12 3 4

13 2 4

样例输出 Sample Output  

39

注释 Hint 

多进程DP

 

题解：想想对于当前已经走了K步，三个棋子的横坐标也已经知道，那么它们的纵坐标......那这三点是怎么走到的？也就是他们的前一步可能是什么。一但确定了走了几步和横坐标，就可以确定下来纵坐标。同样，一旦确定了走了几步和纵坐标，就可以确定下来横坐标。

用f[k,x,y,z]表示当走到第k步时,且三人横坐标分别为x,y,z时..所取数的最大值..由于每一个人都可以由2个方向推来..所以一共有2^3=8种状态

wa因：红色部分，最外层循环必然是k步，内层循环的终值是当前走到了第几步而不是n，因为，走k步时，横坐标最多到k

 

program :

program p1143;
var f:array[0..40,0..20,0..20,0..20]of longint;
    f1,f2:text;
    n,k,k1:longint;
    a:array[1..20,1..20]of longint;
procedure init;
var i,j:longint;
begin

  read(n);k:=2*n-1;
  for i:=1 to n do
    for j:=1 to n do
      read(a[i,j]);
  fillchar(f,sizeof(f),0);
end;
function s(i,a1,a2,a3:longint):longint;
var b1,b2,b3,k1:longint;
begin
  k1:=i+1;
  b1:=k1-a1;b2:=k1-a2;b3:=k1-a3;
{  writeln(b1,b2,b3);}
  if (a1=a2)and(a1=a3) then exit(a[a1,b1]);
  if (a1=a2)or(a2=a3)or(a1=a3) then
  begin
   if (a1=a2) then exit(a[a1,b1]+a[a3,b3]);
   if(a1=a3) then exit(a[a1,b1]+a[a2,b2]);
   if (a2=a3) then exit(a[a1,b1]+a[a2,b2]);
  end;
      exit(a[a1,b1]+a[a2,b2]+a[a3,b3]);
end;
procedure dp;
var i,a1,a2,a3,t,min:longint;
begin
  f[1,1,1,1]:=a[1,1];
  for i:=2 to k do
    for a1:=1 to i do
      for a2:=1 to i do
        for a3:=1 to i do
          begin
             t:=s(i,a1,a2,a3);min:=-1;
{             writeln(t);}
             if f[i-1,a1,a2,a3]>min then min:=f[i-1,a1,a2,a3];
             if f[i-1,a1-1,a2-1,a3-1]>min then min:=f[i-1,a1-1,a2-1,a3-1];
             if f[i-1,a1-1,a2,a3]>min then min:=f[i-1,a1-1,a2,a3];
             if f[i-1,a1,a2-1,a3]>min then min:=f[i-1,a1,a2-1,a3];
             if f[i-1,a1,a2,a3-1]>min then min:=f[i-1,a1,a2,a3-1];
             if f[i-1,a1-1,a2-1,a3]>min then min:=f[i-1,a1-1,a2-1,a3];
             if f[i-1,a1-1,a2,a3-1]>min then min:=f[i-1,a1-1,a2,a3-1];
             if f[i-1,a1,a2-1,a3-1]>min then min:=f[i-1,a1,a2-1,a3-1];
             f[i,a1,a2,a3]:=min+t;
        end;
  writeln(f[k,n,n,n]);
end;
begin
  init;
  dp;

end.

二取方格数

  问题描述   

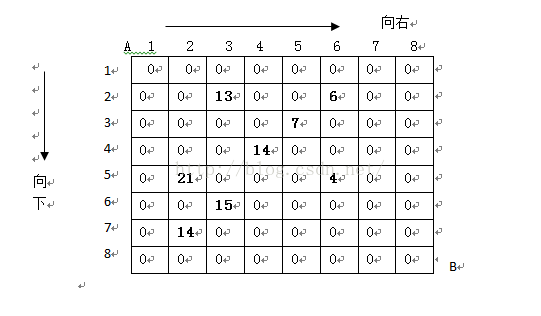
设有N*N的方格图(N<=10,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示（见样例）：

 

 

某人从图的左上角的A 点出发，可以向下行走，也可以向右走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从A点到B 点共走两次，试找出2条这样的路径，使得取得的数之和为最大。

 

   输   入   

输入的第一行为一个整数N（表示N*N的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的0表示输入结束。

 

   输   出   

    只需输出一个整数，表示2条路径上取得的最大的和。

 

   样   例   ：

   输入

      8

      2 3  13

      2 6   6

      3 5   7

      4 4  14

      5 2  21

      5 6   4

6 3  15

6 2  14

0 0  0

 

  输  出

      67

状态表示一：sum[i1,j1,i2,j2]  第一个人到(i1,j1)，第二个人到(i2,j2)时的最大值

 

program 1

program pane;
const maxn=10;
type arraytype=array [0..maxn,0..maxn] of longint;
var i,j,k,n,i1,i2,j1,j2:longint;
    data:arraytype;
    sum:array [0..maxn,0..maxn,0..maxn,0..maxn] of longint;
function max(x,y:longint):longint;
begin
     if x>y then max:=x else max:=y;
end;
BEGIN  {main}
Assign(input,’pane.in’);
Assign(output,’pane.out’);
Reset(input);
Rewrite(output);
     for i:=1 to maxn do
         for j:=1 to maxn do data[i,j]:=0;
     readln(n);
     repeat
           readln(i,j,k);
           data[i,j]:=k
     until (i=0) and (j=0) and (k=0);
     fillchar(sum,sizeof(sum),0);
     for i1:=1 to n do
         for j1:=1 to n do
             for i2:=1 to n do
                 for j2:=1 to n do
                 begin
                      if sum[i1-1,j1,i2-1,j2]>sum[i1,j1,i2,j2]
                         then sum[i1,j1,i2,j2]:=sum[i1-1,j1,i2-1,j2];
                      if sum[i1-1,j1,i2,j2-1]>sum[i1,j1,i2,j2]
                         then sum[i1,j1,i2,j2]:=sum[i1-1,j1,i2,j2-1];
                      if sum[i1,j1-1,i2-1,j2]>sum[i1,j1,i2,j2]
                         then sum[i1,j1,i2,j2]:=sum[i1,j1-1,i2-1,j2];
                      if sum[i1,j1-1,i2,j2-1]>sum[i1,j1,i2,j2]
                         then sum[i1,j1,i2,j2]:=sum[i1,j1-1,i2,j2-1];
                      sum[i1,j1,i2,j2]:=sum[i1,j1,i2,j2]+data[i1,j1];
                      if (i1<>i2) or (j1<>j2)
                         then sum[i1,j1,i2,j2]:=sum[i1,j1,i2,j2]+data[i2,j2]
                 end;
writeln(sum[n,n,n,n]);
close(input);
close(output)
END.

Program 2:

program pfgqz;
var f:array[0..40,0..20,0..20]of longint;
    f1,f2:text;
    n,k,k1:longint;
    a:array[0..20,0..20]of longint;
procedure init;
var i,j,x,y,z:longint;
begin
  assign(f1,'fgqs.in');reset(f1);
  assign(f2,'fgqs.out');rewrite(f2);
  read(f1,n);k:=2*n-1;
  x:=-1;y:=-1;z:=-1;
  while (x<>0)and(y<>0)and(z<>0) do
     begin read(f1,x,y,z);
          a[x,y]:=z;
     end;
  fillchar(f,sizeof(f),0);
end;
function s(i,a1,a2:longint):longint;
var b1,b2,b3,k1:longint;
begin
  k1:=i+1;
  b1:=k1-a1;b2:=k1-a2;
{  writeln(b1,b2,b3);}
  if a1=a2 then exit(a[a1,b1])
    else exit(a[a1,b1]+a[a2,b2]);
end;
procedure dp;
var i,a1,a2,a3,t,min:longint;
begin
  f[1,1,1]:=a[1,1];
  for i:=2 to k do
    for a1:=1 to i do
      for a2:=1 to i do
         begin
             t:=s(i,a1,a2);min:=-1;
{             writeln(t);}
             if f[i-1,a1,a2]>min then min:=f[i-1,a1,a2];
             if f[i-1,a1-1,a2-1]>min then min:=f[i-1,a1-1,a2-1];
             if f[i-1,a1-1,a2]>min then min:=f[i-1,a1-1,a2];
             if f[i-1,a1,a2-1]>min then min:=f[i-1,a1,a2-1];

             f[i,a1,a2]:=min+t;
        end;
  writeln(f2,f[k,n,n]);
end;
begin
  init;
  dp;
  close(f1);
  close(f2);end.