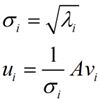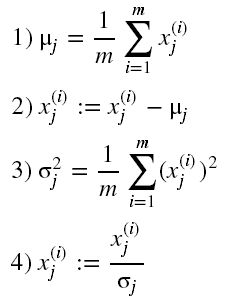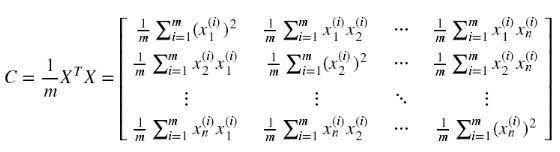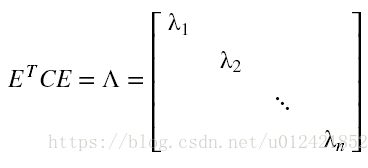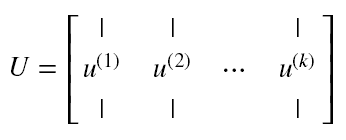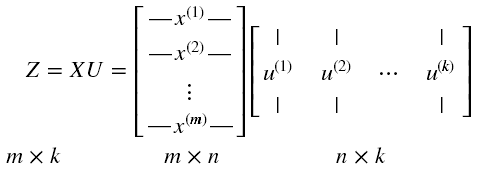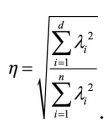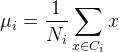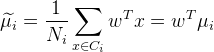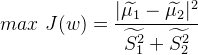算法知识点——（4）降维

一、SVD奇异值分解

1. SVD概述

为什么先介绍SVD算法，因为在后面的PCA算法的实现用到了SVD算法。SVD算法不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。

　　在线性代数中我们学过矩阵（在这里的矩阵必须是n×nn×n的方阵）的特征分解，矩阵A和特征值、特征向量之间的关系如下

　　

将A矩阵做特征分解，特征向量QQ是一组正交向量，具体表达式如下

　　

　　在这里因为QQ中nn个特征向量为标准正交基，满足QT=Q−1QT=Q−1，也就是说QQ为酉矩阵。

　　矩阵的特征值分解的局限性比较大，要求矩阵A必须是方阵（即行和列必须相等的矩阵），那么对于一般的矩阵该如何做分解？

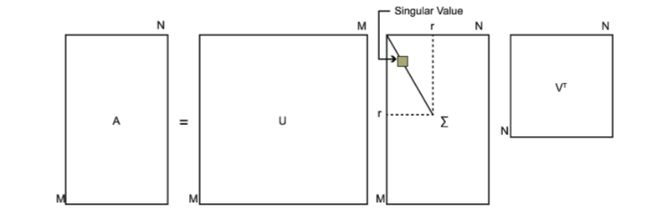
　　奇异值分解就可以处理这些一般性的矩阵，假设现在矩阵A是一个m×nm×n的矩阵，我们可以将它的奇异值分解写成下面的形式

　　

　　在这里UU是m×mm×m的矩阵，ΣΣ是m×nm×n的矩阵（除对角线上的值，其余的值全为0），VV是n×nn×n的矩阵。在这里矩阵UU和VV都是酉矩阵，也就是说满足UTU=IUTU=I，VTV=IVTV=I（其中II为单位矩阵）。对于SVD的定义如下图

　　

　　矩阵ATAATA是一个n×nn×n的方阵，我们对该方阵做特征值分解，可以得到下面的表达式

　　

　　我们将这里得到的向量vivi称为右奇异向量。通过该值我们可以得到uiui（左奇异向量，方阵U中的向量）和σiσi（矩阵ΣΣ中对角线上的值，也就是我们的奇异值）

　　

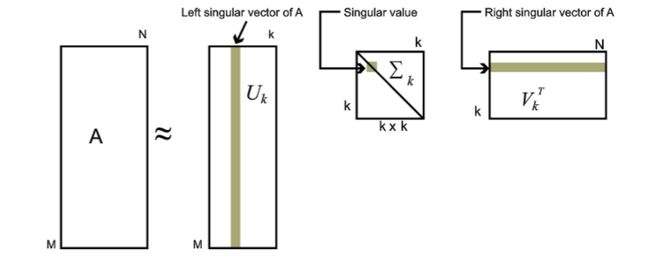
　　对于奇异值，它跟我们特征分解中的特征值相似，在奇异值矩阵ΣΣ中也是按照从大到小排列的，而且奇异值减小的特别快。在很多情况下，前10%甚至前1%的奇异值的和就占总和的99%以上的比例。也就是说我们可以用最大的K个奇异值和对应的左右奇异向量来近似的描述矩阵，如下图所示

　　

　　具体表达式如下

　　Am×n=Um×mΣm×nVTn×n≈Um×kΣk×kVTk×nAm×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT

　　在并行化计算下，奇异值分解是非常快的。但是奇异值分解出的矩阵解释性不强，有点黑盒子的感觉，不过还是在很多领域有着使用。

2. 常见问题

特征值分解和奇异值分解的区别

首先，矩阵可以认为是一种线性变换，而且这种线性变换的作用效果与基的选择有关。

以Ax = b为例，x是m维向量，b是n维向量，m,n可以相等也可以不相等，表示矩阵可以将一个向量线性变换到另一个向量，这样一个线性变换的作用可以包含旋转、缩放和投影三种类型的效应。

奇异值分解正是对线性变换这三种效应的一个析构。

，和是两组正交单位向量，是对角阵，表示奇异值，它表示我们找到了和这样两组基，A矩阵的作用是将一个向量从这组正交基向量的空间旋转到这组正交基向量空间，并对每个方向进行了一定的缩放，缩放因子就是各个奇异值。如果维度比大，则表示还进行了投影。可以说奇异值分解将一个矩阵原本混合在一起的三种作用效果，分解出来了。

而特征值分解其实是对旋转缩放两种效应的归并。（有投影效应的矩阵不是方阵，没有特征值）

特征值，特征向量由得到，它表示如果一个向量v处于A的特征向量方向，那么Av对v的线性变换作用只是一个缩放。也就是说，求特征向量和特征值的过程，我们找到了这样一组基，在这组基下，矩阵的作用效果仅仅是存粹的缩放。对于实对称矩阵，特征向量正交，我们可以将特征向量式子写成，这样就和奇异值分解类似了，就是A矩阵将一个向量从x这组基的空间旋转到x这组基的空间，并在每个方向进行了缩放，由于前后都是x，就是没有旋转或者理解为旋转了0度。

总结一下，特征值分解和奇异值分解都是给一个矩阵(线性变换)找一组特殊的基，特征值分解找到了特征向量这组基，在这组基下该线性变换只有缩放效果。而奇异值分解则是找到另一组基，这组基下线性变换的旋转、缩放、投影三种功能独立地展示出来了。我感觉特征值分解其实是一种找特殊角度，让旋转效果不显露出来，所以并不是所有矩阵都能找到这样巧妙的角度。仅有缩放效果，表示、计算的时候都更方便，这样的基很多时候不再正交了，又限制了一些应用。
 

二. PCA主成分分析

1. PCA概述

PCA是一种线性、非监督、全局的降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，即把原先的n个特征用数目更少的k个特征取代，新特征是旧特征的线性组合。并期望在所投影的维度上数据的方差最大，尽量使新的k个特征互不相关。从旧特征到新特征的映射捕获数据中的固有变异性。以此使用较少的数据维度，同时保留住较多的原数据点的特性。

协方差：可用两个字段的协方差表示其相关性，当cov=0时，表示两个字段完全独立，为使cov=0，第二基只能在与第一基正交方向上选择。

协方差矩阵：

                                                 

                                     

其中，对角线：两个字段的方差     其他元素 ：a和b的协方差

优化目标：

简单来说，PCA将N维向量转换为K维，选择K个单位正交基，使得变换之后：

1. 两两字段协方差等于0
2. 字段的方差尽可能的大

2. PCA原理及求解步骤

PCA降维原理是基于训练数据集X的协方差矩阵C的特征向量组成的K阶矩阵U，XU得到X的k阶降维矩阵Z。
 
主要原理用的是协方差矩阵C是一个实对角矩阵的性质！！！！
 
用到的最重要的性质是：实对角阵的不同特征值对应的特征向量是正交的！！！
 
再结合训练样本集X的理想降维矩阵的特点：每个维度特征线性不相关，即每个维度特征的协方差=0。

 

（1） 对样本数据进行中心化处理，将样本集的中心平移到坐标系的原点O上

（2） 求样本协方差矩阵。协方差矩阵的性质如下：

1. 协方差矩阵C可以对角化
2. 协方差矩阵C的特征值都是实数
3. 协方差矩阵C的特征向量都是实向量
4. 协方差矩阵C的相似对角阵上的元素=协方差矩阵C的特征值
5. 协方差矩阵C的不同特征值对应的特征向量是正交的！！！！

（3） 对协方差矩阵C 进行对角化，特征值分解， 将特征值从大到小排列。

（4） 取特征向量矩阵U 中  特征值前k大对应的特征向量， 通过以下映射将n维样本映射到d维

（5）降维后的新特征矩阵为：

定义降维后的信息占比为

3. 注意事项

注意一：如果使用了PCA对训练集的数据进行了处理，那么对于验证集和测试集也需要进行相对应的处理。

我们在处理训练集的过程中得到了特征的均值 μ 和方差 σ ，以及特征向量 U ，我们需要使用这些参数先对数据进行归一化处理，然后转换到新的特征空间。

注意二：在使用PCA进行压缩之前，先使用原数据进行训练，这样我们才能对比压缩前后的效果。

如果不是占用内存空间太大，或者算法运行速度过慢，其实没有必要进行压缩。

注意三：不要使用PCA来避免过度拟合。

因为通过这样的方式皮避免度拟合，不仅效果很差，并且会丢失部分数据。

4. 常见问题

1. 为什么要算协方差矩阵?

　　根据方差和协方差的计算公式可以看出当均值为0的时候，协方差矩阵=A*AT,这也是为什么要对数据要进行中心化(数据减去均值)的原因（极大简化了协方差矩阵的计算），协方差矩阵是个方阵且是个对称阵，它的的对角线就是方差。方差是反映数据信息量的大小，我们通常说的方差指的是数据在平行于坐标轴上的信息量传播。也就是说每个维度上信息量的传播。这是在二维数据上，如果实在多维数据上，我们要度量数据在多个维度上信息的传播量以及非平行于坐标轴放方向上数据的传播，就是要用协方差表示，从矩阵中我们可以观察到数据在每一个维度上的传播。数据的协方差确定了传播的方向，而方差确定了传播的大小，当然方差和协方差是正相关的。所以说，方差最大的方向就是协方差最大的方向。而协方差的特征向量topX总是指向最大方差的方向，特征向量正交，所以作为一组变换基向量很合适（其实这种逆向推到很蹩脚）。

三、LDA线性判别分析

1. LDA概述

LDA相比PCA更善于对有类别信息的数据进行降维处理，但他对数据的分布做了一些很强的假设，如：每个类数据都是高斯分布、各个类的协方差相等等。尽管这些假设在实际中并不一定满足，但LDA已被证明是非常有效的一种降维方法。主要是因为线性模型对于噪声的鲁棒性比较好，但由于模型简单，表达能力有一定局限性，我们可以通过引入核函数扩展LDA的方法以处理分布较为复杂的数据

（1）目标

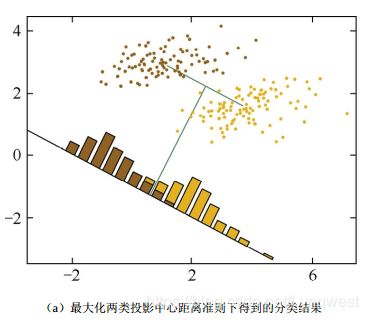
能够最大化类间区分度的坐标轴成分

将特征空间投影到一个维度更小的K维子空间中，同时保持区分类别得信息

（2）原理

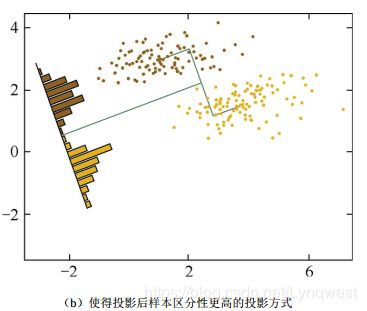
投影到维度更低的空间中，使得投影后的点，会形成按类别区分为一簇一簇的情况；相同类别的点，将会在投影后的空间中更接近

（3）监督性

有监督，计算的是另一类特定的方向，更关心类别

2. 优化目标

                       

找到投影，使得投影后的样本 不同类别之间距离越远越好，同一类别距离越近越好

（1）同一类别越近越好

1. 每类样例均值为： ，  其中i为类别编号
2. 投影后均值表示为：
3. 投影后两类样本中心点尽量分离： 

（2）不同类别之间距离越远越好

1. 越大越好

3. 求解

（1）最大化目标函数

                                     

（2）分子（散列值）展开

                              

       于是 目标函数为

                                     

（4）定义类间散度矩阵    

         定义类内散度矩阵   

（5）于是目标函数为         

（6）最大化 J(w)，对目标函数对w求偏导，令其等于0，得到

（7）由于和是两个数，令 ，则

                                           

由此，最大化的目标对应了一个矩阵的特征值，LDA降维变成了一个求矩阵特征向量的问题，J（w）就对应了矩阵最大的特征值，投影方向就是这个特征值对应的特征向量。

对于二分类问题， 由于，因此的方向始终与一致，如果只考虑w的方向，不考虑长度，可以得到，即只需要求样本的均值和类内方差，马上就可以求出最佳的投影方向w

4. 常见问题

 

 

 

参考文献：

1. 【机器学习】【PCA-1】PCA基本原理和原理推导 + PCA计算步骤讲解 + PCA实例展示数学求解过程

2. 机器学习笔记033 | 主成分分析法（PCA）

3. 机器学习算法总结(九)——降维(SVD, PCA)

4. 《百面机器学习》