用MATLAB实现最短路径问题中的Floyd算法

本文将说明最短路径问题中的Floyd算法原理，以及如何用MATLAB实现。

正文

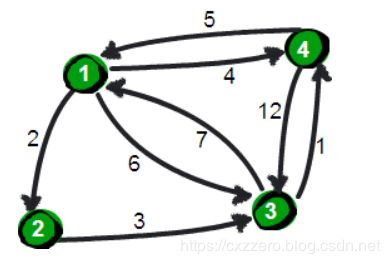
在这幅图中，如果我想知道任意两个点之间的最短距离，有什么好的办法吗？Floyd算法了解一下。

在这个问题中，相邻两个点是“单向”的，也就是说从A点到B点的距离，和从B点到A点的距离不一定相等。Floyd算法可以用来解决这样的单向问题。当然，还有“双向”问题，及相邻两地的距离是固定的，无论出发地是哪个。双向问题显然是单向问题的特例，然而有的算法只能解决双向问题，因此在这里表扬一下Floyd的普适性。

如果我们要从A点到B点，却被禁止中途经过任何其他的点作为中转站的话，我们就只好从A点直接走向B点了。这种情况下的两地最短距离是显而易见的——就是它俩的直接距离嘛。我们规定一下，如果A地点和B地点不相邻的话，那么它俩的直接距离就是无穷大。还有，A点到A点的直接距离是0。

然后我们就可以画一个表格（其实就是之后要用代码建立的矩阵）。就一开始说的这个图而言，我们可以画出如下的表格（表中行号和列号都代表地点的编号。
）。

表格1：

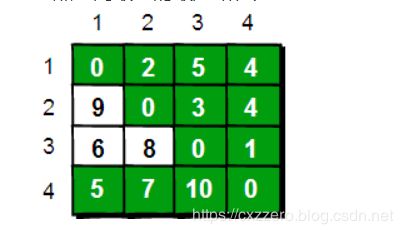
表格中的数字就是两地的直接距离。例如3地点到4地点的直接距离是1。另外，按照我们的规定，1地点和1地点的距离是0，1地点和2地点由于不相邻，所以它俩直接距离是无穷。

这个表格的含义是，在要求不经过任何中转站的条件下，两地之间的最短距离。由于是单向问题，我们规定两地距离是行编号所代表的地点—>列编号所代表的地点。

用MATLAB生成这个表格（矩阵）:
e = [0,2,6,4;Inf,0,3,Inf;7,Inf,0,1;5,Inf,12,0];

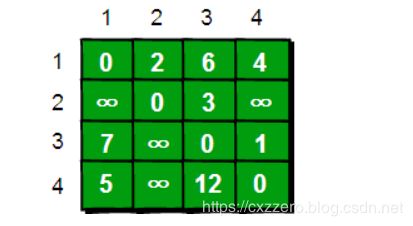
现在增加一个条件，中途最多只能经过1地点作为中转站。在这个条件下，有些地点之间的最短距离就会发生变化。例如，4地点到2地点的最短距离从无穷变成了9，或者是4地点到3地点，最短距离从无穷变成了11。于是我们又可以画出一个新的表。

表格2：

这个表的含义是，在只允许经过1地点的条件下，两地之间的最短距离。可以发现我们一开始画的表格中的一些数字被更新了。

那怎么用代码遍历任意的两点，查看在上述条件下它俩之间的最短距离是否有所更新？以下是代码。

%i表示表格中第i行，j表示第j列
%设一共有n个地点
for i = 1:n %从第一行开始遍历到最后一行
    for j = 1:n %遍历到了某一行后，开始遍历列，从第一列开始遍历到最后一列
        if (e(i,j) > e(i,1) + e(1,j)) 
            e(i,j) = e(i,1) + e(1,j);  %如果i地和j地间通过1地点中转的话距离更近，就将该距离更新为这两地间最短距离
        end
    end
end

现在，如果在允许通过1地点作为中转的条件下，还允许把2地点也作为中转站，试问现在的最短距离？

由于表格2已经蕴含了“允许通过1地点作为中转”的条件了，因此对于附加的这个条件，我们只需在表格2的基础上再进行遍历操作就可以，思想和之前的一样。

以下是代码：

%i表示表格中第i行，j表示第j列
% 下面出现的e代表的是第二个表格
for i = 1:n %从第一行开始遍历到最后一行
    for j = 1:n %遍历到了某一行后，开始遍历列，从第一列开始遍历到最后一列
        if (e(i,j) > e(i,2) + e(2,j))  %如果i地和j地间通过2地点中转的话距离更近，就将该距离更新为这两地间最短距离
            e(i,j) = e(i,2) + e(2,j);   %可以注意到，除了此处，其他部分代码完全一样！
        end
    end
end

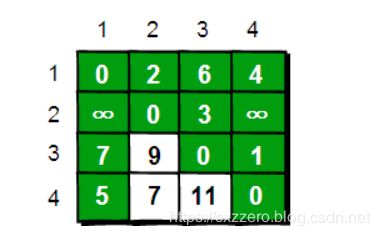
然后我们就获得了第三个表格。

表格3：

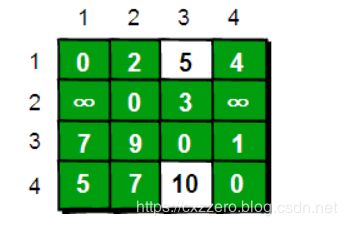
这里(1,3)和(4,3)中的元素作了更新，说明这两地间在允许把1地点作为中转站的基础上，因为再允许添加一个2地点作为中转站而进一步缩短了最短距离。

按照这个思路下去，我们可以逐次增加沿途允许中转的地点，直到囊括所有地点——那岂不就是我们一开始想要解决的问题：在无任何约束下，求两地之间最短距离？

十分好理解对吧。以下就是囊括所有中转站后的代码：

for r = 1:n  %逐个增加中转站，增加n次
    for i = 1:n
        for j = 1:n
            if (e(i,j) > e(i,r) + e(r,j))
                e(i,j) = e(i,r) + e(r,j);
            end
        end
    end
end

最终的结果如下：

迭代完成后，通过表格，任何两地之间的最短距离，我们都可以一目了然。这么好的算法不妨将其生成一个函数吧，方便日后调用：

function [y]=floyd(n,e)
%n 代表 矩阵阶数
%e 代表 初始矩阵
%y 代表 最终矩阵
%----------------------------------------------
for r = 1:n  %逐个增加中转站，增加n次
    for i = 1:n
        for j = 1:n
            if (e(i,j) > e(i,r) + e(r,j))
                e(i,j) = e(i,r) + e(r,j);
            end
        end
    end
end

综上可见，Floyd算法的精髓在于，从一开始不允许走任何的中转地，到慢慢的增加中转地的数量，一步一步的缩短两地之间的最短距离，当允许将所有区域都作为中转地时，我们就达到了目的——即在没有任何约束条件下求两地最短距离！

看到这，相信你已经理解Floyd算法的内核了，也知道了如何用MATLAB实现Floyd算法，并求得最短距离。如果你不必知道最短距离对应的路线，阅读可以到此结束。如果希望进一步获知最短路线到底是什么，请再看下文。

最短路线获取

那如果我们不仅要得到两地之间的最短距离，还想知道对应的最短路线呢？下面我们要对Floyd函数进行小小的改进。

请看代码：

function [e,v]=floyd_plus(n,e,A,B)
%该函数不仅可以用于求最短距离，还可以得到最短距离对应的路径
%n 代表 矩阵阶数
%e 代表 初始矩阵
%y 代表 最终矩阵
%A 代表 出发地编号
%B 代表 目的地编号
%----------------------------------------------
v = []; #用于存储中转站编号
P = zeros(n); %P的作用不太好言简意赅地解释清，应该可以看懂
for r = 1:n  %逐个增加中转站（r为新增的中转站的编号），增加n次
    for i = 1:n
        for j = 1:n
            if (e(i,j) > e(i,r) + e(r,j))
                e(i,j) = e(i,r) + e(r,j);
                P(i,j) = r;  %将该中转站的编号记录到对应位置
            end
        end
    end
end

k = B;
while P(A,k) ~= 0
    v = [v,k];
    k = P(A,k); 
end
v = [v,[k,A]];
v = v(end:-1:1); %倒序，让起点作为第一个元素，终点作为最后一个元素

这是一个强大的算法，在地点达到数十个的时候尤其有用（再多的话写初始矩阵要把手写残了哈哈）下面附上一个该算法的应用，深深的体会Floyd算法的强大吧！
进入后请看第二次作业的题目一和题目二

参考文献

1. Floyd-傻子也能看懂的弗洛伊德算法
2. 已经找到了最短路径长度,但不知道如何输出最短路径所经过的顶点出来!