二叉查找树

参考: 《算法导论》

一棵随机构造的二叉查找树的期望高度为O(logn),从而这种树上基本动态集合操作的平均时间为logn.红黑树是二叉查找树的一种变形。

二叉查找树的性质:设x为二叉查找树中的一个节点.如果y是x的左子树中的一个节点，则key[y]<=key[x].如果y是x的右子树中的一个节点，则key[y]>=key[x].

由二叉查找树的性质可知，中序遍历可以顺序输出树中的所有关键字。

 1 /*中序遍历二叉查找树*/
 2 InOrder_Tree_Walk(x)
 3 {
 4     if(x!=NULL)
 5     {
 6         InOrder_Tree_Walk(left[x]);
 7         print x;
 8         InOrder_Tree_Walk(right[x]);
 9     }
10 }

查找

 1 /*给定树根的指针和关键字k,返回包含关键字k的节点，不存在则返回空*/
 2 Tree_Search(x,k)
 3 {
 4     if(x==NULL||key[x]==k)
 5         return x;
 6     if(k<key[x])
 7         return Tree_Search(left[x],k);
 8     else
 9         return Tree_Search(right[x],k);
10 }

 

最小/大关键字元素

/*返回一个指向以x为根的子树中的最小元素的指针*/
Tree_Minimum(x)
{
    while(left[x]!=NULL)
        x=left[x];
    return x;
}

/*返回一个指向以x为根的子树中的最大元素的指针*/
Tree_Maximum(x)
{
    while(right[x]!=NULL)
        x=right[x];
    return x;
}

 

后继:某一节点x的后继为具有大于key[x]中的关键字中最小者的那个节点。

 1 /*返回节点x的后继节点，如果x是具有最大关键字的节点的话，则返回空*/
 2 Tree_Successor(x)
 3 {
 4     if(right[x]!=NULL)
 5         return Tree_Minimum(right[x]);
 6     y=p[x];    //x的父亲
 7     while(y!=NULL&&x==right[y])
 8     {
 9         x=y;
10         y=p[x];
11     }
12     return y;
13 }

 

前趋:某一节点x的前趋为具有小于key[x]中的关键字中最大者的那个节点。

 1 /*返回节点x的前趋节点，如果x是具有最小关键字的节点的话，则返回空*/
 2 Tree_Predecessor(x)
 3 {
 4     if(left[x]!=NULL)
 5         return Tree_Maximum(left[x]);
 6     y=p[x];    //x的父亲
 7     while(y!=NULL&&x==left[y])
 8     {
 9         x=y;
10         y=p[x];
11     }
12     return y;
13 }

 

对于一棵高度为h的二叉查找树，以上几个操作(除中序遍历外)的复杂度均为O(h).

插入

为将一个新值v插入到二叉查找树T中，可调用过程Tree_Insert.传给该过程的参数是个节点z,并且有key[z]=v,left[z]=NULL,right[z]=NULL。该过程修改了T和z的某些域，并把z插入到树T中适当的位置上。

 1 Tree_Insert(T,z)
 2 {
 3     y=NULL;
 4     x=root[T];
 5     while(x!=NULL)
 6     {
 7         y=x;
 8         if(key[z]<key[x])
 9             x=left[x];
10         else
11             x=right[x];
12     }
13     p[z]=y;
14     if(y==NULL)    //Tree T is empty
15         root[T]=z;
16     else if(key[z]<key[y])
17         left[y]=z;
18     else
19         right[y]=z;
20 }

 

删除

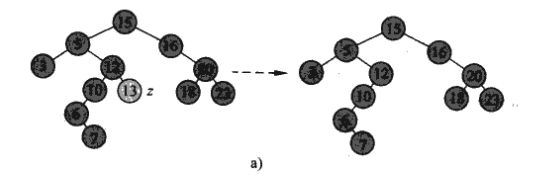
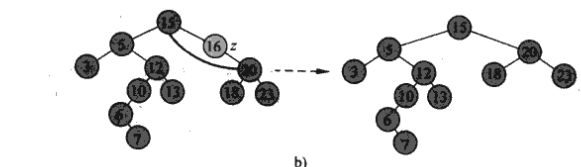
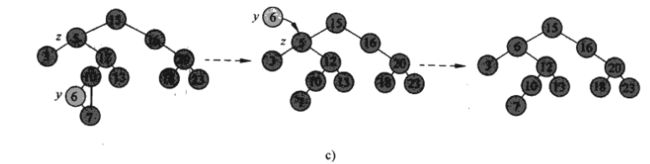
 将节点z从二叉查找树T中删除，有以下三种情况：(1).z没有子女，则修改其父节点p[z],使NULL为其子女；(2).z只有一个子女，则可以通过在其子节点和父节点之间建立一条链来删除z;(3).z有两个子女，则可以先删除z的后继y(由后继的定义可知y一定没有左子女)，再用y的内容代替z的内容。

 

 

 1 Tree_Delete(T,z)
 2 {
 3     if(left[z]==NULL||right[z]==NULL)
 4         y=z;
 5     else
 6         y=Tree_Successor(z);
 7     if(left[y]!=NULL)    //y=z的情况
 8         x=left[y];
 9     else
10         x=right[y];
11     if(x!=NULL)
12         p[x]=p[y];    //在y的子节点和父节点之间建立一条链来删除y
13     if(p[y]==NULL)    //z是树T的根的情况，即要删除树根的情况
14         root[T]=x;
15     else if(y==left[p[y]])
16         left[p[y]]=x;
17     else
18         right[p[y]]=x;
19     if(y!=z)    //z有两个子女的情况,用刚才删除的y的内容代替z的内容，相当于删除了z
20         key[z]=key[y];
21     return y;
22 }

对于高度为h的二叉查找树，动态集合操作插入和删除的时间复杂度为O(h).

《算法导论》上的定理：一棵在n个关键字上随机构造的二叉查找树的期望高度为O(logn)。

另外，还给出了包含n个节点的不同的二叉树(是二叉树，而不仅仅是二叉查找树)的数目：bn=(1/(n+1))*C(2n,n) （即第n个卡特兰数）。证明见《算法导论》。

转载于:https://www.cnblogs.com/kkzone/archive/2013/01/25/2877305.html