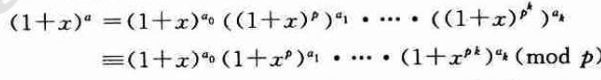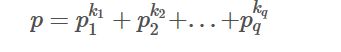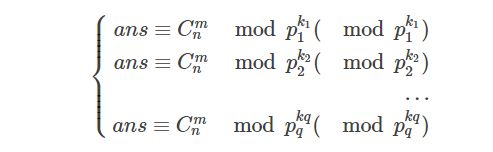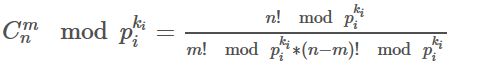【数论-Lucas定理】

1.写在前面：我始终觉得，对于一个问题要知其然，更要知其所以然。Lucas定理在刚刚接触数论的时候就知道了，因为这是一个很常用的定理，常常和中国剩余定理放在一起考。最近在组合数学上出现了很多问题，但是都是找个结论就过去了。浑浑噩噩并不懂其中原理，感觉自己的数学直觉一直在下降，以前我甚至能够从数据中看出来数学表达式，后来学了很多的工具，就变懒了，甚至连一个稍微复杂一点的积分都懒得动手，直接自适应Simpson积过去。今天又拿起了笔，准备把Lucas定理自己证明一遍。证完之后，我似乎又看到之前的那个影子：不畏惧任何数学表达式，即使推导了十几页也毫不畏惧。废话到此结束，正题开始。

2.Lucass定理：

      

Lucas定理是同余理论中的一个很重要的定理，用于组合数取模。常常使用在问题的结果需要对某个数据取模，n，m很大，达到1e15以上，但是p在1e9以内。一般来说最好的效果实在1e5以内。看到这个式子，一个十分典型的递归，并且注意到p是素数。所以我们就会有很多疑问：这个定理怎么来的？p为什么一定要是素数？p不是素数可以吗？我们来解决这些问题。

3.在解决这个问题之前，我想说一个问题：记得是ZOJ的某次月赛吧，问题就是求:.  其实说白了，就是统计杨辉三角形每一行中有多少个奇数。这个问题当时我打了个表，看出了规律。结论和i和n的二进制有关，但是为什么呢？

4.首先证明Lucas定理。

                  Lucas定理在数论中表述是这样的：

                     

解释一下：其实就是把a,b在p进制下表示出来，然后发现C(a,b)是和后边的式子同余的。这个式子写成递归就是上边的递归形式下的Lucas定理。递归形式下的更加易于编程，但是由于递归的存在，p不能过大。问题来了，这个结论怎么来的？继续证明。

----多项式同余-----

首先介绍一个辅助工具：多项式下的同余，其实也很容易：

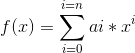
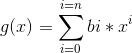         .   其中对于任意的 都有：ai和bi对同余，那么就说这两个多项式是同余的。

知道了这些，我们还需要明白这样一个结论：%n=0,对于所有的成立的条件是：n是质数。这个很容易证明，就不再证了。其实这里也说明了，为什么Lucas定理要求p一定是质数，而且，从这里我们也可以找出来p不是质数该如何处理。这个我们后边再讲。这样我们来看一个性质：

     。这个证明可以用上边的结论证;

  .  我们知道中间的所有项mod p是0，所以只有第一项和最后一项。那么上式得证。

那么我们对于一般的式子：

  我们把a拆分成p进制：

                 

对于这个等式，在等式的左边，我们考虑x的b次方的系数：C(a,b)那么对于右边，其实就是在每个乘积式子中拿出一些凑出b。前边公式我们知道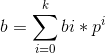：.也就是b在p进制下的拆分，所以对于每一个乘积式子，拿出bi。由乘法原理：C(ai,bi)的乘积即使左边x的b次方的系数。根据多项式相等的原则，我们推出：

                         

到了这里，Lucas定理得证。我们回答了第一个问题，Lucas定理是怎么来的。其实也回答了第二个问题，为什么p要是素数？因为只有p是素数才满足：对于所有的j<=p-1是成立的。那么p不是素数行吗？这个问题我们最后回答，先回答第四个问题：二项式系数：C(n,i)里面对于每一个n到底有多少个奇数？

5.二项式系数奇偶以及更加一般的C(a,b)%p=0的问题。在二项式系数中，判断是不是奇偶，其实是就是在判断:C(n,i)%2==0?.那么根据Lucas定理，这里的素数就是2.我们考虑这个式子：把n,i的二进制数位分别写出来，如果存在ai=bi,相等的时候是显然成立的。大于的时候，这个地方就是C(1,0)=1，乘起来必然是一个奇数。所以猜想得证：C(n,i)%2=1的充分必要条件是：对于i和n的二进制数位，n的每一位必须大于等于i的每一位。然后考虑每一层二项式奇数有多少？假设我用f(x)表示x的二进制数位中1的个数，对于所有的i属于[0,n],C(n,i)%2是奇数的个数就是：pow(2,f(n-1))。为什么？上边我已经证明了80%，接下来可以自己证明。那么这个结论是不是可以推广呢？答案是可以的，因为我们上来其实就说明了一个很重要的观点：a,b需要在p进制下观察，才能更好的认识这个问题。在我们证明二进制下的结论的时候，并没有很特殊的假设，只是建立在2是个质数这个结论上，所以对于所有的质数，都是成立的。那么我们可以得出下边的推论：

对于C(a,b)%p=0,p是质数。这个式子成立的条件是，对于a,b在p进制下的数位:ai,bi.只要存在一对数位使得ai

6.p不是质数的处理：p不是质数，就显得很棘手了。但是我们没有办法修改Lucas定理，所以只能把P变成质数，通过质因数分解

                                

那么列出同余方程：

                                  

得到了这个，我们就可以用中国剩余定理来合并答案。问题转化为如何求：这个式子的值。

我们把组合数展开：

                                  

尝试着把n!中所有pi的倍数分离，然后神奇的性质就出现了。发现n！%pi是有循环节的。这样，我们一边递归n!,一边快速幂即可求出答案。

最后放几个链接：

HDU3037：这是个裸题，直接就是结论了，C(n+m,m)%p.采用Lucas定理即可。

二项式系数奇偶问题。

洛谷Lucas定理模板。

最后，给出HDU3037我AC的代码：

#include
using namespace std;
typedef long long ll;
ll  n, m, p;
ll Ext_gcd(ll a, ll b, ll &x, ll &y) 
{
	if (b == 0) { x = 1, y = 0; return a; }
	ll ret = Ext_gcd(b, a%b, y, x);
	y -= a / b * x;
	return ret;
}
ll Inv(ll a, int m) 
{   
	ll d, x, y, t = (ll)m;
	d = Ext_gcd(a, t, x, y);
	if (d == 1) return (x%t + t) % t;
	return -1;
}

ll Cm(ll n, ll m, ll p)  
{
	ll a = 1, b = 1;
	if (m > n) return 0;
	while (m)
	{
		a = (a*n) % p;
		b = (b*m) % p;
		m--;
		n--;
	}
	return (ll)a*Inv(b, p) % p;  
}

int Lucas(ll n, ll m, ll p)  
{
	if (m == 0) return 1;
	return (ll)Cm(n%p, m%p, p)*(ll)Lucas(n / p, m / p, p) % p;
}

int main()
{
	int  T;
	cin >> T;
	while (T--)
	{
		scanf("%lld%lld%lld", &n, &m, &p);
		printf("%d\n", Lucas(n + m, m, p));
	}
	return 0;
}

参考书籍：冯志刚《初等数论》