数论进阶——kuangbin模板+计蒜客课程指引
- 导言:数论以及基础数学在程序设计竞赛中充当了相当的角色。很多题看似模拟与构造,最终都可归类成数学题目。因此掌握数论的逻辑思维,对于看待程序设计竞赛的题目会有更多简洁而优美的实现技巧。
- 二次修改后的导言:经过不算很缜密的思考后,还是将快速(矩阵)幂和欧拉函数的章节提前了。如果我有幸让读者读到这篇博客,请读者注意一下:欧拉函数与关于质数的章节有部分知识是交错的,大家参考的时候可以交错的看
笔者知识有限,如有纰漏,敬请指出,谢谢!
数论和基础数学
- 快速幂qp和矩阵快速幂s_qp
- 大指数取模
- 矩阵快速幂
- 整除和取余Exact division&Remainder
- 整除
- 取余
- 关于gcd和lcm
- 欧拉函数φ(x)与积性函数Euler&Multiplicative
- 欧拉函数φ(x)
- 积性函数
- 欧拉定理
- 费马小定理
- 其他性质
- 原根primitive root
- 求原根
- 线性筛(同时得到欧拉函数以及素数表)
- 关于质数Prime
- 质数检测法
- 埃式筛法
- 欧式筛法
- 贴一道综合题
- 将一个合数按最小质数依次分解,并统计个数
- Fermat素数测试
- Miller_Rabin素数测试算法
- 二次探测定理优化
- 技巧
- 扩展欧几里得Extra Euclid
- 乘法逆元
- 线性预处理逆元inverse
- 用费马小定理来求逆元(模数是质数)
- 用欧拉定理求逆元(模不一定是质数)
- 无敌初始化(求出阶乘模,乘法逆元,阶乘逆元)
- 中国剩余定理(模线性方程组)
- 样式
- 解法:
- 高斯消元法Gauss elimination
- 高斯消元处理同余方程组
- 傅里叶变换&&数论变换Fourier transform
- 离散傅里叶变换(DFT)&&快速傅里叶变换(FFT)
- 快速数论变换(NTT)
- 母函数(生成函数)Generating function
- 五边形数和欧拉函数和分割函数的那些事
- 求 A^B 的约数之和对 MOD 取模(唯一分解定理和)
- 莫比乌斯反演
- Baby-Step Giant-Step
- 自适应Simpson积分(保证精度的积分算法)
- 斐波那契数列取模循环节
- 其它公式
- Polya
快速幂qp和矩阵快速幂s_qp
快速幂已经很多人介绍过了,相信读者有了解过。也不难懂,直接上代码:
LL qp(LL base,LL n)
{
LL res = 1;
while(n){
if(n&1) res = res * base;
base = base * base;
n>>=1;
}
return res;
}
大指数取模
比如 2 233 m o d 100 2^{233}mod100 2233mod100,不能算出 2 233 2^{233} 2233再去取模。利用同余定理可以写出: ( 2 ∗ 2 ∗ 2... ∗ 2 ) m o d 100 (2*2*2...*2)mod100 (2∗2∗2...∗2)mod100 = ( ( 2 m o d 100 ∗ 2 m o d 100 ) m o d 100... ) m o d 100 ((2mod100*2mod100)mod100...)mod100 ((2mod100∗2mod100)mod100...)mod100那么只需要在快速幂的基础上base与res取模即可。
代码:
LL qp(LL base,LL n,LL mod)
{
LL res = 1;
while(n){
if(n&1) res = (res%mod * base%mod)%mod;
base = (base%mod * base%mod)%mod;
n>>=1;
}
return res;
}
矩阵快速幂
代码:
#include 整除和取余Exact division&Remainder
整除
这里不做过多介绍,大家了解整除符号即可。
定义:设 a , b ∈ Z , a ≠ 0 a,b∈Z,a≠0 a,b∈Z,a̸=0,如果存在 q ∈ Z q∈Z q∈Z使得 b = a q b=aq b=aq,那么就说 b b b可被 a a a整除,记做 a ∣ b a|b a∣b,且称 b b b是 a a a的倍数, a a a是 b b b的约数(也称为除数、因数)。
取余
取余有两套公式,对应乘法与除法。一个整式取模等于每一项因子的取模之和/积再取模。
1. ( a + b ) m o d p = ( a m o d p + b m o d p ) m o d p 1.(a+b) modp=(a modp+bmod p) modp 1.(a+b)modp=(amodp+bmodp)modp
2. ( a × b ) m o d p = ( a m o d p × b m o d p ) m o d p 2.(a×b) modp=(a modp×bmod p) modp 2.(a×b)modp=(amodp×bmodp)modp
关于gcd和lcm
算法不多做介绍了,直接上两题:
练习题:两仪剑法
练习题:取石子游戏
欧拉函数φ(x)与积性函数Euler&Multiplicative
欧拉函数φ(x)
φ ( x ) = x ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) ⋯ ( 1 − 1 p n ) φ(x)=x(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_n}) φ(x)=x(1−p11)(1−p21)⋯(1−pn1)
其中 p 1 , p 2 ⋯ p n p_1,p_2\cdots p_n p1,p2⋯pn是 x x x的所有质因数。
欧拉函数还可以理解为i从1~n 满足 gcd(i,n) = 1 的个数
积性函数
欧拉函数 p ( n ) p(n) p(n)为积性函数,但不是完全积性函数。
欧拉函数有以下几个性质:
1、 φ ( p ) = p − 1 φ(p)=p-1 φ(p)=p−1
2、 φ ( p k ) = p k − p k − 1 = ( p − 1 ) p k − 1 φ(p^k)=p^k-p^{k-1}=(p-1)p^{k-1} φ(pk)=pk−pk−1=(p−1)pk−1
3、若 m , n m,n m,n互质,则有 φ ( m n ) = φ ( m ) φ ( n ) φ(mn)=φ(m)φ(n) φ(mn)=φ(m)φ(n)。
- 质数与质数间一定互质
- 合数与质数间、合数与合数间可能互质
欧拉定理
若 a , n a,n a,n互质,则有 a φ ( n ) ≡ 1 ( m o d n ) a^{φ(n)}≡1(modn) aφ(n)≡1(modn)
费马小定理
a p − 1 = 1 ( m o d p ) a^{p-1}=1(mod p) ap−1=1(modp),其中 p p p为质数, a a a为任意正整数。
其他性质
∑ d ∣ n φ ( d ) = n \sum_{d|n}φ(d) = n d∣n∑φ(d)=n
意思是, 1 1 1~ n n n中,满足 d ∣ n d|n d∣n(即 n ≡ 0 ( M O D d ) n≡0(MODd) n≡0(MODd))的所有 d d d的欧拉函数之和就等于 n n n。
貌似跟莫比乌斯反演有着一定的联系。
原根primitive root
当对一个数字 w w w套欧拉两次,得出的结果极为原根的个数。
N = φ ( φ ( w ) ) N = φ(φ(w)) N=φ(φ(w))
求原根目前的做法只能是从2开始枚举,然后暴力判断g^(P-1) = 1 (mod P)是否当且仅当指数为P-1的时候成立。而由于原根一般都不大,所以可以暴力得到。
原根跟快速数论变换有关(NTT),后文有介绍。
关于原根的定义请见百度百科
求原根
long long a[100005], len;
long long q_pow(long long a, long long b, long long c)
{
long long ans=1;
while(b)
{
if(b%2)
ans=(ans*a)%c;
a=(a*a)%c;
b/=2;
}
return ans;
}
// test if g ^ ((p-1)/a) == 1 (mod p)
long long g_test(long long g, long long p)
{
for(int i=0;i<len;i++)
if(q_pow(g, (p-1)/a[i], p)==1)
return 0;
return 1;
}
long long primitive_root(long long p)
{
// get the prime factor of p-1
len=0;
long long tmp=p-1;
for(long long i=2;i<=tmp/i;i++)
{
if(tmp%i==0)
{
a[len++]=i;
while(tmp%i==0)
tmp/=i;
}
}
if(tmp!=1)
a[len++]=tmp;
// find the primitive root
long long g=1;
while(g<p)
{
if(g_test(g,p))
return g;
g++;
}
}
}
int main()
{
getPrime();
int T;
int P;
scanf("%d",&T);
while(T--)
{
scanf("%d",&P);
solve(P);
}
return 0;
}
线性筛(同时得到欧拉函数以及素数表)
代码:
#include关于质数Prime
质数检测法
算法比较简单,入门同学应该都知道算法优化的逻辑。直接上代码:
int is_prime(int n) {
for (int i = 2; i * i <= n; ++i) {
if (n % i == 0) {
return 0; // 不是质数
}
}
return 1; // 是质数
}
埃式筛法
算法思想可以百度找到,也比较简单,用于筛出一个区间段的所有素数。复杂度小于 O ( n l o g n ) O(nlogn) O(nlogn)大于 O ( n ) O(n) O(n)
代码:
for (int i = 2; i <= n; ++i) {
is_prime[i] = 1;
}
for (int i = 2; i * i <= n; ++i) {
if (is_prime[i]) {
for (int j = i * i; j <= n; j +=i) {
is_prime[j] = 0;
}
}
}
欧式筛法
着重介绍一下这个筛法。它在埃式筛法的基础上,利用了合数最小质因子唯一的思想,只用最小质因子去筛合数,跳过其他因子重复筛选的步骤,从而实现 O ( N ) O(N) O(N)。(不过空间复杂度会比埃式稍大一些)
下面贴代码:
int EulerSieve(int n)
{
int p=0;
//memset(prime,0,sizeof(prime));
//memset(flag,0,sizeof(false));不需要初始化,不需要重复标记
for(int i=2; i<=n; i++)
{
//记录质因数i。
if(flag[i]==0) ///flag==1代表其为合数
prime[++p]=i;
//筛掉i的倍数(无论i为质数还是合数)
for(int j=1; j<=p&&i*prime[j]<=n; j++)///每次都把prime有的质因数提取出来筛一遍
{
flag[i*prime[j]]=1;
if(i%prime[j]==0) ///下面着重介绍
break;
}
}
return p;
}
上面代码结合了埃式筛法,可以说是埃式筛法的进阶版,所以基本看懂代码意思应该没问题。可能难理解的地方在这里:
if(i%prime[j]==0) break;
我们进一步思考,实际上他跳过了下一步 i ∗ p r i m e [ j + 1 ] i*prime[j+1] i∗prime[j+1]以及下m步(直到循环结束)的 i ∗ p r i m e [ j + m ] i*prime[j+m] i∗prime[j+m]。那么为什么 i ∗ p r i m e [ j + 1 ] i*prime[j+1] i∗prime[j+1]代表的和数不需要筛除呢?原因是如果 i i i能被 p r i m e [ j ] prime[j] prime[j]整除,说明 i i i是 p r i m e [ j ] prime[j] prime[j]的整数倍,即 i = p r i m e [ j ] ∗ k , ( k ∈ N ∗ ) i=prime[j] * k,(k∈N^*) i=prime[j]∗k,(k∈N∗),那么 i ∗ p r i m e [ j + 1 ] i*prime[j+1] i∗prime[j+1]就可以写成 p r i m e [ j ] ∗ k ∗ p r i m e [ j + 1 ] prime[j] * k * prime[j+1] prime[j]∗k∗prime[j+1]。由此可知,一个本应该由 p r i m e [ i ] prime[i] prime[i]来筛选的合数就不应该被 i ∗ p r i m e [ j + 1 ] i * prime[j+1] i∗prime[j+1] 访问到,而是这个合数应该交给 p r i m e [ j ] prime[j] prime[j]来筛选、跳过不必要的重复筛,那么就实现了 O ( n ) O(n) O(n)筛法。
贴一道综合题
POJ-2689
题解略,上代码:
#include将一个合数按最小质数依次分解,并统计个数
其实就是得到素数组prime后依次相除即可。可以进行 p r i m e [ i ] ∗ p r i m e [ i ] < = x prime[i]*prime[i]<=x prime[i]∗prime[i]<=x来进行 O ( n ) O(\sqrt{n}) O(n)优化。因为根据素数判断法的思想,如果1~prime[i]都没有筛出最后的因子,那么这个数一定是个1*temp的质数(或者为1),直接将这个数放到下一行即可。
代码:
#includeFermat素数测试
参考博客:pi9nc的博客
人们在检验费马小定理(如果一个数是质数p,那么满足 a p − 1 = 1 ( m o d p ) a^{p-1}=1(mod p) ap−1=1(modp))的逆命题的时候,发现了 2 340 ≡ 1 ( m o d 341 ) 2^{340} ≡1(mod341) 2340≡1(mod341),但341 = 11 * 31。而后人们发现561, 645, 1105等数都表明当底数a=2的时候费马小定理的逆命题不成立,所以人们把所有能够整除 2 n − 1 − 1 2^{n-1} - 1 2n−1−1的合数 n n n称作伪素数。
不满足 2 n − 1 ≡ 1 ( m o d n ) 2^{n-1}≡1(modn) 2n−1≡1(modn)的n一定不是素数(2是个例外,要注意这一点);如果满足的话则多半是素数。意思即是, 2 n − 1 ≡ 1 ( m o d n ) 2^{n-1}≡1(modn) 2n−1≡1(modn)是一个数n是素数的必要条件。一个比试除法效率更高的素性判断方法出现了:将伪素数表制出来,当 n n n满足 2 n − 1 ≡ 1 ( m o d n ) 2^{n-1}≡1(modn) 2n−1≡1(modn)且又不在伪素数表里,就说明 n n n是素数。
质数与伪质数的关系:
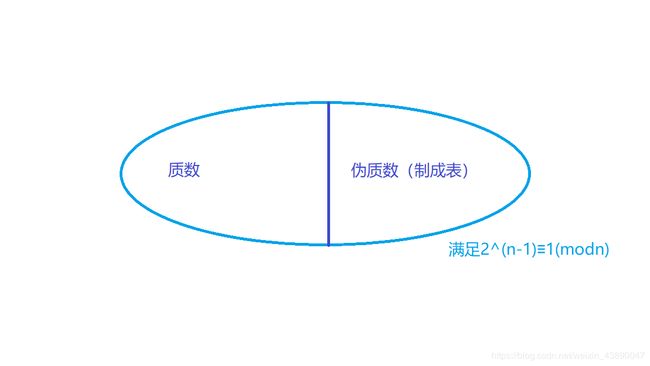
之所以这种方法更快,是因为我们可以使用二分法快速计算 2 n − 1 m o d n 2^{n-1}modn 2n−1modn的值(快速幂,下文有介绍)。
但我们并不真正需要构造出一个伪素数表。人们发现,一个合数在a=2时通过了测试,在a=3的时候的计算结果却排除了可能。于是,人们将伪素数的定义改为:满足 a n − 1 m o d n = 1 a^{n-1} mod n = 1 an−1modn=1的合数 n n n叫做以 a a a为底的伪素数(pseudoprime to base a)。(注意,能够整除底数a的质数的小费马式子结果都为0。)
那么选取小于待测数的正整数a作为底数,对其作关于底数a的小费马式子测试,只要一个式子不通过,就把它扔回合数世界中。这就是Fermat素性测试。
费马小定理毕竟只是素数判定的一个必要条件.满足费马小定理条件的整数n未必全是素数.有些合数也满足费马小定理的条件.这些合数被称作Carmichael数,前3个Carmichael数是561,1105,1729. Carmichael数是非常少的.在1~100000000范围内的整数中,只有255个Carmichael数.
利用下面的二次探测定理可以对上面的素数判定算法作进一步改进,以避免将Carmichael数当作素数.
Miller_Rabin素数测试算法
二次探测定理优化
Miller和Rabin两个人的工作让Fermat素性测试迈出了革命性的一步,建立了Miller-Rabin素性测试算法。新的测试基于下面的定理:
如果p是素数,x是小于p的正整数,且 x 2 ≡ 1 ( m o d p ) x^2≡1(modp) x2≡1(modp),那么要么 x = 1 x=1 x=1,要么 x = p − 1 x=p-1 x=p−1。
这是显然的,因为 x 2 ≡ 1 ( m o d p ) x^2≡1(modp) x2≡1(modp) 相当于p能整除 x 2 − 1 x^2-1 x2−1,也即 p p p能整除 ( x + 1 ) ( x − 1 ) (x+1)(x-1) (x+1)(x−1)。
p p p整除 ( x + 1 ) (x+1) (x+1)(此时 x = p − 1 x = p - 1 x=p−1)或 ( x − 1 ) (x-1) (x−1)(此时 x x x只能为 1 1 1)
我们下面来演示一下上面的定理如何应用在Fermat素性测试上。前面说过341可以通过以2为底的Fermat测试,因为 2 340 m o d 341 = 1 2^{340} mod 341=1 2340mod341=1。如果341真是素数的话,那么 2 170 m o d 341 2^{170}mod 341 2170mod341只可能是1或340;当算得 2 170 m o d 341 2^{170} mod 341 2170mod341确实等于1时,我们可以继续查看 2 85 2^{85} 285除以341的结果。我们发现, 2 85 m o d 341 = 32 2^{85} mod 341=32 285mod341=32,这一结果摘掉了341头上的素数皇冠
过程:
对于341这个数字:以a=2作为基数,进行如下测试
b e g i n 2 340 m o d 341 ⇒ 1 b e c a u s e ( 340 m o d 2 = = 0 ) ⇓ g o 2 170 m o d 341 ⇒ 1 b e c a u s e ( 170 m o d 2 = = 0 ) ⇓ g o 2 85 m o d 341 ⇒ 32 e n d begin\\ 2^{340} mod 341\Rightarrow 1\\ because(340mod2==0)\Downarrow go\\ 2^{170}mod 341\Rightarrow 1\\ because(170mod2==0)\Downarrow go\\ 2^{85} mod 341\Rightarrow 32\\ end begin2340mod341⇒1because(340mod2==0)⇓go2170mod341⇒1because(170mod2==0)⇓go285mod341⇒32end
这就是Miller-Rabin素性测试的方法。不断地提取指数n-1中的因子2,把n-1表示成 d ∗ 2 r d*2^r d∗2r(其中d是一个奇数)。那么我们需要计算的东西就变成了 a d ∗ 2 r a^{d*2^r} ad∗2r除以n的余数。于是,要么等于1,要么等于n-1(那就是素数,跳出)。 a d ∗ 2 r a^{d*2^r} ad∗2r如果等于1,定理继续适用于 a d ∗ 2 r − 1 a^{d*2^{r-1}} ad∗2r−1,这样不断开方开下去,直到对于某个i满足 a d ∗ 2 r − i m o d n = n − 1 a^{d*2^{r-i}}modn=n-1 ad∗2r−imodn=n−1或者最后指数中的2用完了得到的 a d m o d n = n − 1 或 者 = 1 a^{d}modn=n-1 或者 = 1 admodn=n−1或者=1(满足质数,跳出)。这样,Fermat小定理加强为如下形式:
尽可能提取因子2,把 n − 1 n-1 n−1表示成 d ∗ 2 r d*2^r d∗2r,如果n是一个素数,那么 a d m o d n = 1 a^{d}modn = 1 admodn=1,或者存在某个i使得 a d ∗ 2 r − i m o d n = n − 1 a^{d*2^{r-i}}modn=n-1 ad∗2r−imodn=n−1 ( 0 < = i < r 0<=i<r 0<=i<r) (注意i可以等于0,这就把 a d m o d n = n − 1 a^{d}modn=n-1 admodn=n−1的情况统一到后面去了)
Miller-Rabin素性测试同样是不确定算法,我们把可以通过以a为底的Miller-Rabin测试的合数称作以a为底的强伪素数(strong pseudoprime)。第一个以2为底的强伪素数为2047。第一个以2和3为底的强伪素数则大到1 373 653。
Miller-Rabin算法的代码也非常简单:计算d和r的值(可以用位运算加速,即快速积,快速幂),然后二分计算 a d m o d n a^dmodn admodn的值,最后把它平方r次。
代码:
/*对应hoj 1356 Prime Judge*/
#include 技巧
对于大数的素性判断,目前Miller-Rabin算法应用最广泛。一般底数仍然是随机选取,但当待测数不太大时,选择测试底数就有一些技巧了。比如,如果被测数小于4 759 123 141,那么只需要测试三个底数2, 7和61就足够了。当然,你测试的越多,正确的范围肯定也越大。如果你每次都用前7个素数(2, 3, 5, 7, 11, 13和17)进行测试,所有不超过341 550 071 728 320的数都是正确的。如果选用2, 3, 7, 61和24251作为底数,那么 1 0 16 10^{16} 1016内唯一的强伪素数为46 856 248 255 981。这样的一些结论使得Miller-Rabin算法在OI中非常实用。通常认为,Miller-Rabin素性测试的正确率可以令人接受,随机选取k个底数进行测试算法的失误率大概为 4 ( − k ) 4^{(-k)} 4(−k)。
扩展欧几里得Extra Euclid
扩展欧几里得算法是用来在已知a,b的情况下求解一组特解 x , y x,y x,y,使它们满足等式: a x + b y = g c d ( a , b ) = d ax+by=gcd(a,b)=d ax+by=gcd(a,b)=d (gcd 表示最大公约数,该方程的解一定存在)。
exgcd最后要求出 x , y , d x,y,d x,y,d,d来自exgcd返回的结果。
x = y 1 , y = x 1 − a b × y 1 , d = e x g c d ( ) x=y_1,y=x_1-\frac{a}{b}×y_1,d = exgcd() x=y1,y=x1−ba×y1,d=exgcd()
int exgcd(int a, int b, int &x, int &y) {
if(b == 0) {
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int t = x; x = y; y = t - a / b * y;
return d;
}
那么对于 a x + b y = c ax + by = c ax+by=c这个方程来说,只有 d ∣ c d|c d∣c的情况下此方程才有解,而通解为 x = c d x 0 + k b d , y = c d y 0 − k a d x=\frac{c}{d}x_0+k\frac{b}{d},y=\frac{c}{d}y_0-k\frac{a}{d} x=dcx0+kdb,y=dcy0−kda
乘法逆元
给定两个整数a和p。假设存在一个x使得 a x ≡ 1 ( m o d p ) ax≡1(modp) ax≡1(modp)。那么我们称 x x x为 a a a关于 p p p的乘法逆元。对于逆元的求法,可以借助扩展欧几里得,把上面的式子变形一下,变成 a x + k p = 1 ax+kp=1 ax+kp=1。就可以用扩展欧几里得就出一个 x x x。并且,我们也可以发现, a a a关于 p p p的逆元存在的充要条件是 g c d ( a , p ) = 1 gcd(a,p)=1 gcd(a,p)=1,也就是 a a a和 p p p必须互质。
在知乎上看到一种说法,逆元在方程中的作用就是为了消去对应参数的作用,将其置为1,这个作用的理解听上去比较通俗易懂,尚不知是否符合。
那么我们可以这样理解,在modp的环境下,一个数的倒数就可以表示成关于模p的逆元。比如 1 ( n − m ) ! m o d p = i n v [ ( n − m ) ! ] m o d p \frac{1}{(n-m)!}modp = inv[(n-m)!] modp (n−m)!1modp=inv[(n−m)!]modp那么这时候表示分母就容易许多(因为我们可以在整数域下处理倒数)。
线性预处理逆元inverse
求出 i ( i ∈ 1 − n ) i(i∈1-n) i(i∈1−n)关于 p p p的逆元。
直接上代码:
// p 必须为质数,p / i 为整除。
inv[1] = 1;
for (int i = 2; i <= n; ++i) {
inv[i] = (p - p / i) * inv[p % i] % p;
}
应用:
求组合数取模的时候可以用到。
令 f a c t i = 1 ∗ 2 ∗ 3 … i m o d p , i n v s i = i n v 1 ∗ i n v 2 … i n v i m o d p fact_i=1 * 2 * 3…i modp,inv_{s_i}=inv_1*inv_2…inv_imodp facti=1∗2∗3…imodp,invsi=inv1∗inv2…invimodp
C n m m o d p = n ! m ! ( n − m ) ! m o d p = f a c t n ⋅ i n v s m ⋅ i n v s n − m m o d p C^{m}_{n}modp =\frac{n!}{m!(n-m)!}modp=fact_n·inv_{s_m}·inv_{s_{n-m}}modp Cnmmodp=m!(n−m)!n!modp=factn⋅invsm⋅invsn−mmodp
没有题目。一般的扩展欧几里得题目比较容易写出方程,只要注意如何取模至正数的方法,以及边界值0的情况即可。
用费马小定理来求逆元(模数是质数)
逆元的方程: a x ≡ 1 ( m o d p ) ax≡1(modp) ax≡1(modp)
费马小定理的方程: a p − 1 ≡ 1 ( m o d p ) a^{p-1} ≡ 1(modp) ap−1≡1(modp)
发现两者可以联立: a x ≡ a p − 1 ( m o d p ) ax ≡ a^{p-1}(modp) ax≡ap−1(modp)得到如下方程:
x ≡ a p − 2 ( m o d p ) x ≡ a^{p-2}(modp) x≡ap−2(modp)
之后用快速幂便可求得逆元。
(当模数是质数,其实就是欧拉定理的特殊情况)
用欧拉定理求逆元(模不一定是质数)
根据欧拉定理,只要 a , m a,m a,m互质,那么就有 a φ ( m ) ≡ 1 ( m o d m ) a^{φ(m)}≡1(modm) aφ(m)≡1(modm)将其变形一下,即有 a ∗ a φ ( m ) − 1 ≡ 1 ( m o d m ) a*a^{φ(m)-1}≡1(modm) a∗aφ(m)−1≡1(modm),那么对于a关于p的逆元就是 a φ ( m ) − 1 a^{φ(m)-1} aφ(m)−1。线性求出欧拉数,然后套快速幂。
无敌初始化(求出阶乘模,乘法逆元,阶乘逆元)
用来求组合数取模问题。巨强。
void init()
{
fact[0] = fact[1] = 1;
fiv[0] = fiv[1] = 1; ///fiv是阶乘逆元
inv[1] = 1;
for(int i = 2; i <= maxn; ++i)
{
//递推保存fact阶乘,递推求inv和fiv各个逆元
fact[i] = fact[i-1]*i%mod;
inv[i] = (mod-mod/i)*inv[mod%i]%mod;
fiv[i] = inv[i]*fiv[i-1]%mod;
}
}
中国剩余定理(模线性方程组)
《孙子算经》中这样提到:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
这句话的意思就是,一个整数除以三余二,除以五余三,除以七余二,问这个整数的值是多少。因为《孙子算经》中首次提出了这种问题并给出了具体的解法,所以中国剩余定理也叫小子定理。
样式
中国剩余定理的一元模线性方程组如下:
S : { x = a 1 ( m o d m 1 ) x = a 2 ( m o d m 2 ) ⋮ x = a n ( m o d m n ) S : \begin{cases} x=a1(mod m1)\\ x=a2(mod m2)\\ \vdots\\ x=an(mod mn)& \end{cases} S:⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x=a1(modm1)x=a2(modm2)⋮x=an(modmn)
解法:
中国剩余定理定义:假设整数 m 1 , m 2 , … , m n m_1,m_2,…,m_n m1,m2,…,mn两两互质,则方程组S一定有解,通解可以构造如下:
设 M = m 1 × m 2 × … × m n = ∏ i = 1 n m i M=m_1×m_2×…×m_n=\prod_{i=1}^{n}m_i M=m1×m2×…×mn=∏i=1nmi,
并设 M i = M / m i M_i=M/m_i Mi=M/mi, t i = M − 1 t_i=M^{-1} ti=M−1,表示 M i M_i Mi模 m i m_i mi意义下的倒数,
即 M i ∗ t i ≡ 1 ( m o d m i ) M_i*t_i≡1(modm_i) Mi∗ti≡1(modmi)(即 M i ∗ t i + k ∗ m i = 1 M_i*t_i + k*m_i=1 Mi∗ti+k∗mi=1)。
那么方程式的通解可以写作:
x = a 1 t 1 M 1 + a 2 t 2 M 2 + … + a n t n M n + k M = ∑ i = 1 n a i t i M i + k M x=a_1t_1M_1+a_2t_2M_2+…+a_nt_n M_n+kM=\sum_{i=1}^{n}a_it_iM_i+kM x=a1t1M1+a2t2M2+…+antnMn+kM=∑i=1naitiMi+kM
从方程式中我们可以知道,唯一没有确定下来的参数是 t i t_i ti,而根据恒等式 M i ∗ t i ≡ 1 ( m o d m i ) M_i*t_i≡1(modm_i) Mi∗ti≡1(modmi),我们可以得出等式 M i ∗ t i + k ∗ m i = 1 M_i*t_i + k*m_i=1 Mi∗ti+k∗mi=1,那么我们就根据扩展欧几里得算法将 t i t_i ti求出。
代码:(前提是模数两两互质)
int CRT(int a[], int m[], int n) {
int M = 1;
int ans = 0;
for(int i = 1; i <= n; i++) {
M *= m[i];
}
for(int i = 1; i <= n; i++) {
int x, y;
int Mi = M / m[i];
exgcd(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;///记得要取模,这是在取模的条件下得出的t_i(t_i即为x)
}
if(ans < 0) ans += M;
return ans;
}
不互质模方程组模板:(因为我也没研究明白,就不讲了)
代码:
/**
中国剩余定理(不互质)
*/
#include 高斯消元法Gauss elimination
这篇博客写的很好pengwill97的博客,我觉得比我要讲要好很多哈哈哈。不懂高斯消元法的原理可以看这篇博客。
浮点数代码:
#include 网上有用高斯消元法解决开关问题的。我个人目前遇到的开关问题,都能用状态压缩dp中的滚动dp和子集dp完成题目。如果有兴趣了解开关问题怎样构建方程的,可以看kuangbin写的poj-1681的题解。这里就不贴出来了。
高斯消元处理同余方程组
多元一次同余方程的写法: a 0 + a 1 x 1 + a 2 x 2 + . . . a n − 1 x n − 1 ≡ b ( m o d m ) a_0+a_1x_1+a_2x_2+...a_{n-1}x_{n-1}≡b(modm) a0+a1x1+a2x2+...an−1xn−1≡b(modm)
记不记得同余方程的定义?其实就是恒等式两方同时取模后的值是相等的。其实只需要在高斯消元的基础上逐项取个模即可。
代码:
观察下面取模的地方。
#include傅里叶变换&&数论变换Fourier transform
离散傅里叶变换(DFT)&&快速傅里叶变换(FFT)
参考了此博客:胡小兔的OI博客
这篇博客写的很好了,我觉得我写不出这样的高度。不过在此留下两点要点:
- 1、题目的条件或暗含条件都是给了 a 0 到 a n − 1 a_0到a_{n-1} a0到an−1的,这个不是你要求的东西。
- 2、现将式子构造成点值函数,再将式子变回向量 a 0 . a 1 , . . . , a n − 1 {a_0.a_1,...,a_{n-1}} a0.a1,...,an−1形式。求解过程已经涉及了傅里叶变换和傅里叶逆变换了。
那么这里贴上一个十进制的高精度乘法 ( n l o g 2 n ) (nlog_2n) (nlog2n)。其实对于一些高难度的傅里叶题目,做不出来也没问题,因为需要一定的数学基础。但这个高精度乘法代表的算法实质已经很明了了。就算不清楚递归与蝴蝶变换,只要理解了原理,然后在题目中又能够造出多项式,那么就要考虑来一个FFT了。
#include
void read(T &x){
char c;
bool op = 0;
while(c = getchar(), c < '0' || c > '9')
if(c == '-') op = 1;
x = c - '0';
while(c = getchar(), c >= '0' && c <= '9')
x = x * 10 + c - '0';
if(op) x = -x;
}
template
void write(T x){
if(x < 0) putchar('-'), x = -x;
if(x >= 10) write(x / 10);
putchar('0' + x % 10);
}
*/
const int N = 1000005;
const double PI = acos(-1);
typedef complex <double> cp;
char sa[N], sb[N];
int n = 1, lena, lenb, res[N];
cp a[N], b[N], omg[N], inv[N];
void init(){
for(int i = 0; i < n; i++){
omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
inv[i] = conj(omg[i]); ///conj求omg的共轭复数
}
}
void fft(cp *a, cp *omg){
int lim = 0;
while((1 << lim) < n) lim++;
for(int i = 0; i < n; i++){
int t = 0;
for(int j = 0; j < lim; j++)
if((i >> j) & 1) t |= (1 << (lim - j - 1));
if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
for(int l = 2; l <= n; l *= 2){
int m = l / 2;
for(cp *p = a; p != a + n; p += l){
for(int i = 0; i < m; i++){
cp t = omg[n / l * i] * p[i + m];
p[i + m] = p[i] - t;
p[i] += t;
}
}
}
}
int main(){
scanf("%s%s", sa, sb);
lena = strlen(sa), lenb = strlen(sb);
while(n < lena + lenb) n<<=1;
///lena+lenb指的是卷积后的总长度。我们挑选的n应该是2^i同时要大于卷积长
for(int i = 0; i < lena; i++)
a[i].real(sa[lena - 1 - i] - '0');///读到的第一位数是最高位的
for(int i = 0; i < lenb; i++)
b[i].real(sb[lenb - 1 - i] - '0');
init();
fft(a, omg);
fft(b, omg); ///依次对两个函数进行FFT
for(int i = 0; i < n; i++)
a[i] *= b[i]; ///让两个快速傅里叶转换数的系数依次相乘。鉴于C(x) = A(x) * B(x)///为卷积做好准备
fft(a, inv); ///对最后一个傅里叶数进行共轭转换。乘omega的倒数,即为其共轭复数
for(int i = 0; i < n; i++){
res[i] += floor(a[i].real() / n + 0.5);
res[i + 1] += res[i] / 10;
res[i] %= 10;
}
///res就是最后的卷积结果,他来自于傅里叶转换的实部
///得到res再按顺序输出的话,相当于对每个系数都乘了对应的10^k,相当于带了x=10进去
for(int i = res[lena + lenb - 1] ? lena + lenb - 1: lena + lenb - 2; i >= 0; i--)
putchar('0' + res[i]);
enter;
return 0;
}
高精度乘法作用的卷积就是每个对应位置的数。比如 12345 12345 12345中的 2 2 2,它就代表在在千位数上出现了两次,最后我们将它归到 a 3 a_3 a3( a i a_i ai从零开始第四位)就应该等于2。相当于数与数之间有x的高阶差。
再贴一道,kuangbin的HDU 4609,1e5个木棒,任取三根组成三角形的概率。
题以及题解:kuangbin的博客题解
(求组合(以和的形式)的个数,考虑用卷积,然后用傅里叶转换来实现)
代码:
#include 快速数论变换(NTT)
FFT毕竟是在复数领域上作用的,对于一些整数类型用傅里叶做卷积的话会有精度损失。那么对于整数做卷积的题目,那么这时候就应该使用NTT了。(关于模数的选取用下面的P,或者P=998244353也没问题)
上个高精度乘法取模的代码:
#include 母函数(生成函数)Generating function
刚开始学习母函数的时候,对于多项式乘积来表示组合情况的时候,我以为是傅里叶变换,但对于傅里叶转换应用基本局限在一重组合***甚至不用傅里叶*** (比如给你几个数,问你有多少种,例如 1 , 3 , 4 , 4 , 4 1,3,4,4,4 1,3,4,4,4,一共有三类( 1 , 3 , 4 1,3,4 1,3,4))和二重组合(给你几个数,再给你另一个集合的几个数,让你求组合(相加)后有几种情况,比如{ 1 , 2 , 3 1,2,3 1,2,3}和{ 4 , 5 , 5 4,5,5 4,5,5},他们组合就有{5,6,7,8}四种情况)。对于二重组合来说,FFT可以将算法优化到 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)级别,在二重组合上很是优秀。但是在解决多重组合上面就不行了。
(我又双找了别人的博客,没办法写得好啊哈哈哈哈)这片博客介绍了…
把要点提炼出来,即为:
- 1、指数对应种类序列,系数对应计数序列
- 2、根据第一点,我们可以知道观察问题的流程:①关注问题的种类序列②其对应的计数序列要写全
- 3、母函数是计数工具,x的取值我们不关心,似乎只是个占位置的东西
引入母函数的目的,其实是给了我们将复杂问题映射为简单问题的多一种思路(尤其是对于组合问题来说)。而**多项式的乘法运算(系数相乘,指数相加)**使母函数具有了计数能力。
其实母函数是可以用背包 d p dp dp来实现的。但它(母函数)作为最基础而优雅的暴力解法,它通常能给背包 d p dp dp提供最初始的思路,而背包 d p dp dp算法要做的就是优化这个暴力思路,包括空间和时间上。
比如整数拆分题:HDU-1028,就可以用以下的母函数代码做:
#include有个跟编程无关,但很有意思的推理:斐波那契求通项。
斐波那契通项公式
下面我们用生成函数求斐波那契数列的通项公式:
首先 f ( x ) = x + x 2 + 2 x 3 + 3 x 4 + 5 x 5 + . . . f(x)=x+x^2+2x^3+3x^4+5x^5+... f(x)=x+x2+2x3+3x4+5x5+...
将 f ( x ) f(x) f(x)乘上个 x x x,然后相减
f ( x ) − x ∗ f ( x ) = ( x + x 2 + 2 x 3 + 3 x 4 + . . . ) − ( x 2 + x 3 + 2 x 4 + 3 x 5 + . . . ) = x + x 3 + x 4 + 2 x 5 + 3 x 6 + . . . = x + x 2 f ( x ) f(x)−x∗f(x)=(x+x^2+2x^3+3x^4+...)-(x^2+x^3+2x^4+3x^5+...)=x+x^3+x^4+2x^5+3x^6+...=x+x^2f(x) f(x)−x∗f(x)=(x+x2+2x3+3x4+...)−(x2+x3+2x4+3x5+...)=x+x3+x4+2x5+3x6+...=x+x2f(x)
解 f ( x ) f(x) f(x)得 f ( x ) = x 1 − x − x 2 f(x)=\frac{x}{1-x-x^2} f(x)=1−x−x2x
然后如何还原成序列呢?
先因式分解
x 1 − x − x 2 = x ( 1 − 1 − 5 2 x ) ( 1 − 1 + 5 2 x ) \frac{x}{1-x-x^2}=\frac{x}{(1-\frac{1-\sqrt{5}}{2}x)(1-\frac{1+\sqrt{5}}{2}x)} 1−x−x2x=(1−21−5x)(1−21+5x)x
用裂项法 1 n ( n + k ) = 1 k ( 1 n − 1 n + k ) \frac{1}{n(n+k)}=\frac{1}{k}(\frac{1}{n}-\frac{1}{n+k}) n(n+k)1=k1(n1−n+k1)得
x ( 1 − 1 − 5 2 x ) ( 1 − 1 + 5 2 x ) = 1 ( 1 − 1 − 5 2 x ) ( ( 1 − 1 − 5 2 x + ( − 5 x ) ) x = 1 − 5 ( 1 1 − 1 − 5 2 x − 1 1 − 1 + 5 2 x ) = − 1 5 1 1 − 1 − 5 2 x + 1 5 1 1 − 1 + 5 2 x \frac{x}{(1-\frac{1-\sqrt{5}}{2}x)(1-\frac{1+\sqrt{5}}{2}x)}\\ \large=\frac{1}{(1-\frac{1-\sqrt{5}}{2}x)((1-\frac{1-\sqrt{5}}{2}x+(-\sqrt{5}x))}x\\ \large=\frac{1}{-\sqrt{5}}(\frac{1}{1-\frac{1-\sqrt{5}}{2}x}-\frac{1}{1-\frac{1+\sqrt{5}}{2}x})\\ \large=-\frac{1}{\sqrt{5}}\frac{1}{1-\frac{1-\sqrt{5}}{2}x}+\frac{1}{\sqrt{5}}\frac{1}{1-\frac{1+\sqrt{5}}{2}x} (1−21−5x)(1−21+5x)x=(1−21−5x)((1−21−5x+(−5x))1x=−51(1−21−5x1−1−21+5x1)=−511−21−5x1+511−21+5x1
把他分裂成等比数列的形式。
a n = − 1 5 ( 1 − 5 2 ) n + 1 5 ( 1 + 5 2 ) n a_n=-\frac{1}{\sqrt{5}}(\frac{1-\sqrt{5}}{2})^n+\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^n an=−51(21−5)n+51(21+5)n
这就是斐波那契数列通项公式。
五边形数和欧拉函数和分割函数的那些事
hrhguanli的博客里面介绍清楚了五边形数和欧拉函数的关系,但看不了wiki百科的同学可能会疑惑分割函数是什么。分割函数主要是对于将一个正整数拆分成m个数这类问题所提出的名词,若不加限定, p ( n ) p(n) p(n)就代表将n拆分成其他数之和的方案个数。对于严格的分割函数定义,wiki做出了解释:
一个正整数可以写成一些正整数的和。在数论上,跟这些和式有关的问题称为整数拆分、整数剖分、整数分割、分割数或切割数(英语:Integer partition)。其中最常见的问题就是给定正整数 n n n,求不同数组
( a 1 , a 2 , . . . , a k ) {\displaystyle (a_{1},a_{2},...,a_{k})} (a1,a2,...,ak)的数目,符合下面的条件:
a 1 + a 2 + . . . + a k = n {\displaystyle a_{1}+a_{2}+...+a_{k}=n} a1+a2+...+ak=n(k的大小不定)
a 1 ≥ a 2 ≥ . . . ≥ a k > 0 {\displaystyle a_{1}\geq a_{2}\geq ...\geq a_{k}>0} a1≥a2≥...≥ak>0
其他附加条件(例如限定“ k k k是偶数”,或“ a i a_{i} ai不是 1 1 1就是 2 2 2”等)
分割函数 p ( n ) p(n) p(n)是求符合以上第一、二个条件的数组数目。
那么看了那个博客,应该就能知道五边形数在分割函数的应用了。直接上模板(n拆成其他数之和的方案):
//HDU 4651
//把数 n 拆成几个数(小于等于 n)相加的形式,问有多少种拆法。
#include限制:拆出来的数个数小于等于k:
证明:poursoul的博客——【HDU】4658 Integer Partition【生成函数——数拆分】
代码:
//数 n(<=10^5) 的划分,相同的数重复不能超过 k 个。
#include求 A^B 的约数之和对 MOD 取模(唯一分解定理和)
思路(没研究透):kuangbin的博客
//参考 POJ 1845
//里面有一种求1+p+p^2+p…^3+p^n的方法。
//需要素数筛选和合数分解的程序,需要先调用 getPrime();
#include莫比乌斯反演
我又来转载别人的博客啦。因为自己现学缘故,所以没了解透。
别人的博客:大番茄番茄茄的博客
贴一道题:
B Z O J 2301 BZOJ2301 BZOJ2301
对于给出的 n 个询问,每次求有多少个数对 ( x , y ) (x, y) (x,y),满足 a < = x < = b , c < = y < = d a <= x <= b, c <= y <= d a<=x<=b,c<=y<=d,且 g c d ( x , y ) = k gcd(x, y) = k gcd(x,y)=k, g c d ( x , y ) gcd(x, y) gcd(x,y) 函数为 x x x和 y y y 的最大公约数。 1 < = n < = 50000 , 1 < = a < = b < = 50000 , 1 < = c < = d < = 50000 , 1 < = k < = 50000 1 <= n <= 50000, 1 <= a <= b <= 50000, 1 <= c <= d <= 50000, 1 <= k <= 50000 1<=n<=50000,1<=a<=b<=50000,1<=c<=d<=50000,1<=k<=50000
代码:
#includeBaby-Step Giant-Step
没看懂。求 a x = b ( m o d n ) a^x = b (mod n) ax=b(modn)的 x x x在 [ 0 , n ) [0,n) [0,n)的解 x x x。
上道题:
POJ 2417,3243
#include自适应Simpson积分(保证精度的积分算法)
介绍:xyz32768的博客
代码模板:
double simpson(double a,double b)
{
double c = (a + b) / 2;
return (F(a) + 4*F(c) + F(b))*(b-a)/6;//F()是函数,返回函数值
}
double asr(double a,double b,double eps,double A)
{
double c = (a + b) / 2;
double L = simpson(a,c), R = simpson(c,b);
if(fabs(L + R - A) <= 15*eps)
return L + R + (L + R - A)/15.0;
return asr(a,c,eps/2,L) + asr(c,b,eps/2,R);
}
double asr(double a,double b,double eps)
{
return asr(a,b,eps,simpson(a,b));
}
斐波那契数列取模循环节
必要时要上 unsigned long long
HDU3977
mezhuangzhuang的博客带你了解二次剩余。
代码:
#include其它公式
Polya
我没整理,很大几率用不上bababababa…