算法竞赛专题解析（3）：并查集

本系列文章将于2021年整理出版，书名《算法竞赛专题解析》。
前驱教材：《算法竞赛入门到进阶》 清华大学出版社 2019.8
网购：京东 当当      作者签名书

如有建议，请加QQ 群：567554289，或联系作者QQ：15512356

  本篇包括：
  （1）1~3节，是《算法竞赛入门到进阶》书中原有的内容。
  （2）4节“带权并查集”，是扩展内容。

0 并查集简介

  并查集（Disjoint Set）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。经典的应用有：连通子图、最小生成树Kruskal算法[ 参考本书第10章“10.10.2 kruskal算法”。]和最近公共祖先（Least Common Ancestors, LCA）等。
  并查集在算法竞赛中极为常见。
  通常用“帮派”的例子来说明并查集的应用背景。一个城市中有n个人，他们分成不同的帮派；给出一些人的关系，例如1号、2号是朋友，1号、3号也是朋友，那么他们都属于一个帮派；在分析完所有的朋友关系之后，问有多少帮派，每人属于哪个帮派。给出的n可能是10⁶的。
  读者可以先思考暴力的方法，以及复杂度。如果用并查集实现，不仅代码很简单，而且复杂度可以达到O(logn)。
  并查集：将编号分别为1~n的n个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。在这个集合中，并查集的操作有：初始化、合并、查找。
  本文比较全面地介绍了并查集：
  （1）并查集的基本操作。
  （2）并查集的优化：合并和路径压缩。
  （3）带权并查集。
  并查集的基本应用是集合问题；加上权值之后，利用并查集的合并和查询优化，可以对权值所代表的具体应用进行高效的操作。

1 并查集的基本操作

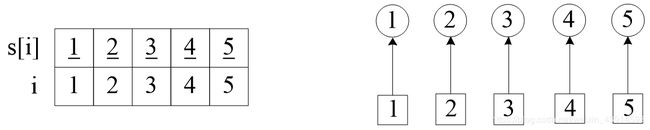
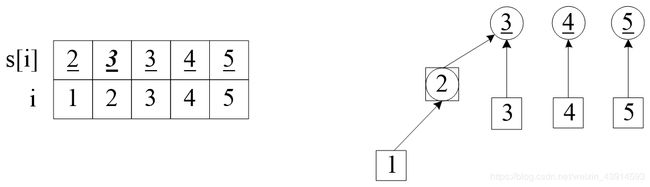
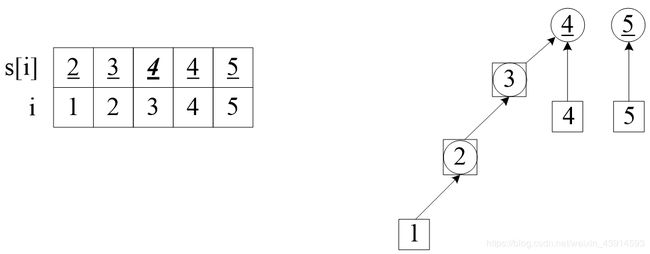
  （1）初始化。定义数组int s[]是以结点i为元素的并查集，开始的时候，还没有处理点与点之间的朋友关系，所以每个点属于独立的集，并且以元素i的值表示它的集s[i]，例如元素1的集s[1]=1。
  下面是图解，左边给出了元素与集合的值，右边画出了逻辑关系。为了便于讲解，左边区分了结点i和集s：把集的编号加上了下划线；右边用圆圈表示集，方块表示元素。

图1 并查集的初始化   （2）合并，例如加入第一个朋友关系(1, 2)。在并查集s中，把结点1合并到结点2，也就是把结点1的集1改成结点2的集2。

图2 合并(1, 2)   （3）合并，加入第二个朋友关系(1, 3)。查找结点1的集，是2，再递归查找元素2的集是2，然后把元素2的集2合并到结点3的集3。此时，结点1、2、3都属于一个集。右图中，为简化图示，把元素2和集2画在了一起。

图3 合并(1, 3)   （4）合并，加入第三个朋友关系(2, 4)。结果如下，请读者自己分析。

图4 合并(2, 4)   （5）查找。上面步骤中已经有查找操作。查找元素的集，是一个递归的过程，直到元素的值和它的集相等，就找到了根结点的集。从上面的图中可以看到，这棵搜索树的高度，可能很大，复杂度是O(n)的，变成了一个链表，出现了树的“退化”现象。   （6）统计有多少个集。如果s[i] = i，这是一个根结点，是它所在的集的代表；统计根结点的数量，就是集的数量。

∎例题
  下面以hdu 1213为例子，实现上述操作。http://acm.hdu.edu.cn/showproblem.php?pid=1213
  有n个人一起吃饭，有些人互相认识。认识的人想坐在一起，而不想跟陌生人坐。例如A认识B，B认识C，那么A、B、C会坐在一张桌子上。
  给出认识的人，问需要多少张桌子。
  一张桌子是一个集，合并朋友关系，然后统计集的数量即可。下面的代码是并查集操作的具体实现。

#include 
using namespace std;
const int maxn = 1050;
int s[maxn];
void init_set(){                 //初始化
   for(int i = 1; i <= maxn; i++)
        s[i] = i;
}
int find_set(int x){               //查找
    return x==s[x]? x:find_set(s[x]);
}
void merge_set(int x, int y){    //合并
    x = find_set(x);
    y = find_set(y);
    if(x != y) s[x] = s[y];     //把x合并到y上，y的根成为x的根
}
int main (){
    int t, n, m, x, y;
    cin >> t;
    while(t--){
        cin >> n >> m;
        init_set();
        for(int i = 1; i <= m; i++){
            cin >> x >> y;
            merge_set(x, y);
        }
        int ans = 0;
        for(int i = 1; i <= n; i++)   //统计有多少个集
            if(s[i] == i)
                ans++;
        cout << ans <<endl;
    }
    return 0;
}

  复杂度：上述程序，查找find_set()、合并merge_set()的搜索深度是树的长度，复杂度都是O(n)，性能比较差。下面介绍合并和查询的优化方法，优化之后，查找和合并的复杂度都小于O(logn)。

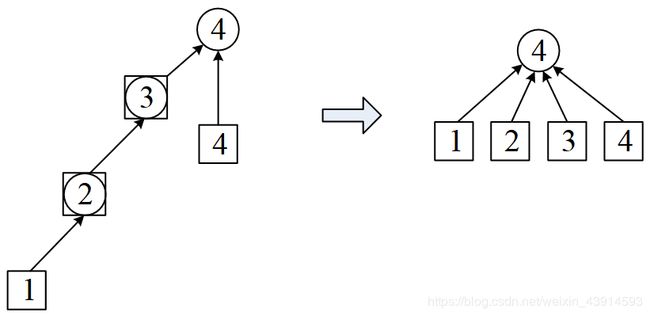
2 合并的优化

  合并元素x和y时，先搜到它们的根结点，然后再合并这两个根结点，即把一个根结点的集改成另一个根结点。这两个根结点的高度不同，如果把高度较小的集合并到较大的集上，能减少树的高度。下面是优化后的代码，在初始化时用height[i]定义元素i的高度，在合并时更改。

int height[maxn];
void init_set(){
   for(int i = 1; i <= maxn; i++){
        s[i] = i;
        height[i]=0;                     //树的高度
   }
}
void merge_set(int x, int y){         //优化合并操作
    x = find_set(x);
    y = find_set(y);
    if (height[x] == height[y]) {
        height[x] = height[x] + 1;      //合并，树的高度加一
        s[y] = x;       
    }
    else{                            //把矮树并到高树上，高树的高度保持不变
        if (height[x] < height[y])  s[x] = y;
        else   s[y] = x;
    }
}

3 查询的优化——路径压缩

  在上面的查询程序find_set()中，查询元素i所属的集，需要搜索路径找到根结点，返回的结果是根结点。这条搜索路径可能很长。如果在返回的时候，顺便把i所属的集改成根结点，那么下次再搜的时候，就能在O(1)的时间内得到结果。

图5 路径压缩

  程序如下：

int find_set(int x){
    if(x != s[x]) 
       s[x] = find_set(s[x]);   //路径压缩
    return s[x];
}

   这个方法称为路径压缩，因为整个搜索路径上的元素，在递归过程中，从元素i到根结点的所有元素，它们所属的集都被改为根结点。路径压缩不仅优化了下次查询，而且也优化了合并，因为合并时也用到了查询。
  上面代码用递归实现，如果数据规模太大，担心爆栈，可以用下面的非递归代码：

int find_set(int x){
    int r = x;
    while ( s[r] != r ) r=s[r];  //找到根结点
    int i = x, j;
    while(i != r){         
         j = s[i];     //用临时变量j记录
         s[i]= r ;     //把路径上元素的集改为根结点
         i = j;
    }
    return r;
}

4 带权并查集

  前面讲解了并查集的基本应用：处理集合问题。并查集的高效，主要是利用了合并和查询的优化。在这些基本应用中，点之间只有简单的归属关系，而没有权值。如果在点之间加上权值，并查集的应用会更广泛。
  如果读者联想到树这种数据结构，会发现，并查集实际上是在维护若干棵树。并查集的合并和查询优化，实际上是在改变树的形状，把原来“细长”的、操作低效的大量“小树”，变成了“粗短”的、操作高效的少量“大树”。如果在原来的“小树”上，点之间有权值，那么经过并查集的优化之变成“大树”后，这些权值的操作也变得高效了。

4.1 带权值的路径压缩和合并

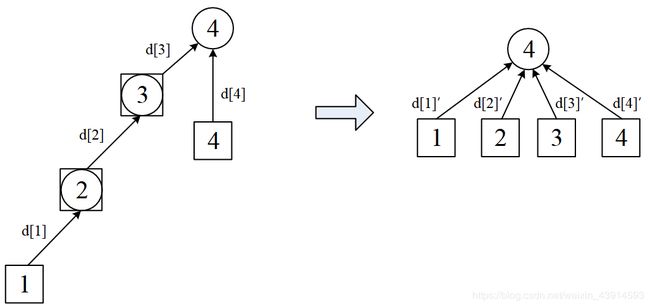
  定义一个权值数组d[]，结点i到父结点的权值为记为d[i]。
  （1）带权值的路径压缩
   下面的图，是加上权值之后的路径压缩。原来的权值d[]，经过压缩之后，更新为d[]’，例如d[1]’=d[1]+d[2]+d[3]。
   需要注意的是，这个例子中，权值是相加的关系，比较简单；在具体的题目的中，可能有相乘、异或等等符合题意的操作。

图6 带权值的路径压缩

  相应地，在这个权值相加的例子中，把路径压缩的代码改为：

int find_set(int x){
    if(x != s[x]) {
         int t = s[x];            //记录父结点
         s[x] = find_set(s[x]);   //路径压缩。递归最后返回的是根结点
         d[x] += d[t];            //权值更新为x到根节点的权值
     }
     return s[x];
}

  注意代码中的细节。原来的d[x]是点x到它的父结点的权值，经过路径压缩后，x直接指向根节点，d[x]也更新为x到根结点的权值。这是通过递归实现的。
  代码中，先用t记录x的原父结点；在递归过程中，最后返回的是根节点；最后将当前节点的权值加上原父结点的权值（注意：经过递归，此时父结点也直接指向根节点，父结点的权值也已经更新为父结点直接到根结点的权值了），就得到当前节点到根节点的权值。
  （2）带权值的合并
   在合并操作中，把点x与到点y合并，就是把x的根结点fx合并到y的根结点fy。在fx和fy之间增加权值，这个权值要符合题目的要求。

4.2 例题

   下面用2个经典例题讲解带权并查集，hdu 3038和poj 1182。
  （1）例题1：hdu 3038
∎问题描述
  给出区间[a, b]，区间之和为v。输入m组数据，每输入一组，判断此组条件是否与前面冲突，最后输出与前面冲突的数据的个数。比如先给出[1, 5]区间和为100，再给出区间[1, 2]的和为200，肯定有冲突。
∎题解
  本题是本节讲解的带权值并查集的直接应用。如果能想到可以把序列建模为并查集，就能直接套用模板了。

#include 
using namespace std;
const int maxn =200010;
int s[maxn];       //集合
int d[maxn];       //权值：记录当前结点到根结点的距离
int ans;

void init_set(){                  //初始化
   for(int i = 0; i <= maxn; i++)
   {   s[i] = i; d[i] = 0;  }
}
int find_set(int x){              //带权值的路径压缩
    if(x != s[x]) {
         int t = s[x];            //记录父结点
         s[x] = find_set(s[x]);   //路径压缩。递归最后返回的是根结点
         d[x] += d[t];            //权值更新为x到根节点的权值
     }
    return s[x];
}

void merge_set(int a, int b,int v){    //合并
    int roota = find_set(a), rootb = find_set(b);
    if(roota == rootb){
       if(d[a] - d[b] != v)
          ans++;
    }
    else{
       s[roota] = rootb;    //合并
       d[roota] = d[b]- d[a] + v;
    }
}

int main(){
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        init_set();
        ans = 0;
        while(m--){
            int a,b,v;
            scanf("%d%d%d",&a,&b,&v);
            a--;
            merge_set(a, b, v);
        }
        printf("%d\n",ans);
    }
    return 0;
}

  （2）例题2：poj 1182 食物链 http://poj.org/problem?id=1182
∎问题描述
  动物王国中有三类动物A、B、C，这三类动物的食物链是：A吃B，B吃C，C吃A。
  现有N个动物，以1~N编号。每个动物都是A、B、C中的一种，但是我们并不知道它到底是哪一种。
  有人用两种说法对这N个动物所构成的食物链关系进行描述：
  第一种说法是"1 X Y"，表示X和Y是同类。
  第二种说法是"2 X Y"，表示X吃Y。
  此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
  1） 当前的话与前面的某些真的话冲突，就是假话；
  2） 当前的话中X或Y比N大，就是假话；
  3） 当前的话表示X吃X，就是假话。
  你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。
∎题解
  这一题中的权值比较有趣，它不是上一题中相加的关系。把权值d[]记录为两个动物在食物链上的相对关系。下面用d(A->B)表示A、B的关系，d(A->B) = 0表示同类，d(A->B) = 1表示A吃B，d(A->B) = 2表示A被B吃。
  这一题难点在权值的更新。考虑三个问题：
  （i）路径压缩时，如何更新权值。
  若d(A->B) =1，d(B->C) = 1，求d(A->c)。因为A吃B，B吃C，那么C应该吃A，得d(A->C)=2；
  若d(A->B) =2，d(B->C) =2，求d(A->c)。因为B吃A，C吃B，那么A应该吃C，得d(A->C)=1；
  若d(A->B) = 0，d(B->C) =1，求d(A->c)。因为A、B同类，B吃C，那么A应该吃C，得d(A->C)=1；
  找规律知：d(A->C) = (d(A->B) + d(B->C) ) % 3，因此关系值的更新是累加再模3。
  （ii）合并时，如何更新权值。本题的权值更新是取模操作，内容见下面的代码。
  （iii）如何判断矛盾。如果已知A与根节点的关系，B与根节点的关系，如何求A、B之间的关系？内容见下面的代码。
  下面是代码。

#include 
#include 
using namespace std;
const int maxn = 50005;

int s[maxn];    //集合
int d[maxn];    // 0：同类； 1：吃； 2：被吃
int ans;

void init_set(){                  //初始化
     for(int i = 0; i <= maxn; i++)
     {   s[i] = i; d[i] = 0;  }
}
int find_set(int x){              //带权值的路径压缩
    if(x != s[x]) {
         int t = s[x];            //记录父结点
         s[x] = find_set(s[x]);   //路径压缩。递归最后返回的是根结点
         d[x] = (d[x] + d[t]) % 3;     //权值更新为x到根节点的权值
     }
    return s[x];
}
void merge_set(int x, int y, int relation){       //合并
 	  int rootx = find_set(x);
 	  int rooty = find_set(y);
	  if (rootx == rooty){
		  if ((relation - 1) != ((d[x] - d[y] + 3) % 3))  //判断矛盾
				ans++;
	  }
	  else {
			s[rootx] = rooty;   //合并
			d[rootx] = (d[y] - d[x] + relation  - 1) % 3;   //更新权值
	  }
}

int main(){
	int n, k;  cin >> n >> k;
    init_set();
	ans = 0;
	while (k--){
		int relation, x, y;
		scanf("%d%d%d",&relation,&x,&y);
		if ( x > n || y > n || (relation == 2 && x == y ) )
			ans++;
		else
            merge_set(x,y,relation);
	}
	cout << ans;
	return 0;
}

5 习题

poj 2524 Ubiquitous Religions，并查集简单题。
poj 1611 The Suspects，简单题。
poj 1703 Find them, Catch them。
poj 2236 Wireless Network。
poj 2492 A Bug’s Life。
poj 1988 Cube Stacking。
poj 1182食物链，经典题。
hdu 3635 Dragon Balls。
hdu 1856 More is better。
hdu 1272 小希的迷宫。
hdu 1325 Is It A Tree。
hdu 1198 Farm Irrigation。
hdu 2586 How far away，最近公共祖先，并查集+深搜。
hdu 6109 数据分割，并查集+启发式合并。

6 参考文献

poj 1182的不同解法，参考[1][2]：
[1]《算法竞赛进阶指南》李煜东，河南电子音像出版社，用“扩展域”的并查集求解poj1182。
[2]《挑战程序设计竞赛》秋叶拓哉，人民邮电出版社，用普通并查集求解poj1182。
[3]leetcode上有一个并查集题目集：https://leetcode-cn.com/tag/union-find/