LIBSVM在Matlab下的使用
支持向量机(SVM,Support Vector Machine)是一种基于统计学习理论的模式识别方法,在解决小样本、高维度及非线性的分类问题中应用非常广泛。
LIBSVM是一个由台湾大学林智仁(Lin Chih-Jen)教授等开发的SVM模式识别与回归的软件包,使用简单,功能强大,本文主要介绍其在Matlab中的使用。
一 安装
1. 下载
在LIBSVM的主页上下载最新版本的软件包,并解压到合适目录中。
参考网站:
libsvm库下载:http://www.csie.ntu.edu.tw/~cjlin/libsvm/
视频:http://v.youku.com/v_showMini/id_XMjc2NTY3MzYw_ft_131.html (有小问题,等下会提到)
详解:http://www.matlabsky.com/thread-11925-1-1.html
更多细节可查看
https://sites.google.com/site/kittipat/libsvm_matlab
2. 编译(这里遇到的问题和liblinear类似)
如果你使用的是64位的操作的系统和Matlab,那么不需要进行编译步骤,因为自带软件包中已经包含有64位编译好的版本:libsvmread.mexw64、libsvmwrite.mexw64、svmtrain.mexw64、svmpredict.mexw64。否则,需要自己编译二进制文件。
目的:将libsvm-3.11\matlab 中 libsvmwrite.c 等 C++文件编译成 libsvmread.mexw32 等matlab文件,这样就可以在command window中被直接调用了。
注意:在最外面的Readme中有提到已经有编译好的文件,比如在libsvm-3.11\windows中也会看到libsvmread.mexw32,但这里不要被误导!还是需要你自己再编译一遍的!(还有如果matlab版本太低,如matlab 7.0是不能用VS作为编译器的,只能用VC++ 6.0,这是我劝你给matlab升级吧!别装vc了~我就是这样,升级到Matlab 2011b就可以用VS2008做编译器了)
首先在Mtlab中进入LIBSVM根目录下的matlab目录(如C:\libsvm-3.17\matlab),在命令窗口输入
>>mex –setup
然后Matlab会提示你选择编译mex文件的C/C++编译器,就选择一个已安装的编译器,如Microsoft Visual C++ 2010。之后Matlab会提示确认选择的编译器,输入y进行确认。
然后可以输入以下命令进行编译。
>>make
注意,Matlab或VC版本过低可能会导致编译失败,建议使用最新的版本。
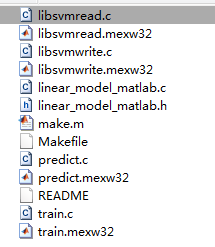
编译成功后,当前目录下会出现若干个后缀为mexw64(64位系统)或mexw32(32位系统)的文件。
同时,可以看到在当前目录下生成类似下图中的文件
对应的train.mexw32和predict.mexw32是svmtrain.mexw32和svmpredict.mexw32
到这一步,Liblinear安装成功。
3. 重命名(可选,但建议执行)
编译完成后,在当前目录下回出现svmtrain.mexw64、svmpredict.mexw64(64位系统)或者svmtrain.mexw32、svmpredict.mexw32(32位系统)这两个文件,把文件名svmtrain和svmpredict相应改成libsvmtrain和libsvmpredict。
这是因为Matlab中自带有SVM的工具箱,而且其函数名字就是svmtrain和svmpredict,和LIBSVM默认的名字一样,在实际使用的时候有时会产生一定的问题,比如想调用LIBSVM的变成了调用Matlab SVM。
如果有进行重命名的,以后使用LIBSVM时一律使用libsvmtrain和libsvmpredict这两个名字进行调用。
4. 添加路径
为了以后使用的方便,建议把LIBSVM的编译好的文件所在路径(如C:\libsvm-3.17\matlab)添加到Matlab的搜索路径中。具体操作为:(中文版Matlab对应进行)
HOME -> Set Path -> Add Folder -> 加入编译好的文件所在的路径(如C:\libsvm-3.17\matlab)
当然也可以把那4个编译好的文件复制到想要的地方,然后再把该路径添加到Matlab的搜索路径中。
二 测试
LIBSVM软件包中自带有测试数据,为软件包根目录下的heart_scale文件,可以用来测试LIBSVM是否安装成功。
有两个数据集,一个是C++的, 一个是matlab的。libsvm库中下载的是C++数据,
所以matlab加载我们下载的heart_scale是会报错的:<这就是视频中遗漏的小问题>
- ??? Error using ==> load
- Number of columns on line 3 of ASCII file D:\ZJU projects\machine learning\libsvm-3.11\heart_scale must be the same as previous lines.
法1、下载matlab数据集(http://download.csdn.net/detail/abcjennifer/4215779)
法2、用libsvmread而非load,就是这里
这里的heart_scale文件不能用Matlab的load进行读取,需要使用libsvmread读取。
进入LIBSVM的根目录运行以下代码(因为heart_scale文件没有被添加进搜索路径中,其他路径下无法访问这个文件):
[heart_scale_label, heart_scale_inst] = libsvmread('heart_scale');
model = libsvmtrain(heart_scale_label, heart_scale_inst, '-c 1 -g 0.07');
[predict_label, accuracy, dec_values] = libsvmpredict(heart_scale_label, heart_scale_inst, model);
如果LIBSVM安装正确的话,会出现以下的运行结果,显示正确率为86.6667%。
* optimization finished, #iter = 134 nu = 0.433785 obj = -101.855060, rho = 0.426412 nSV = 130, nBSV = 107 Total nSV = 130 Accuracy = 86.6667% (234/270) (classification)
三 原理简介
使用SVM前首先得了解SVM的工作原理,简单介绍如下。
SVM(Support Vector Machine,支持向量机)是一种有监督的机器学习方法,可以学习不同类别的已知样本的特点,进而对未知的样本进行预测。
SVM本质上是一个二分类的算法,对于n维空间的输入样本,它寻找一个最优的分类超平面,使得两类样本在这个超平面下可以获得最好的分类效果。这个最优可以用两类样本中与这个超平面距离最近的点的距离来衡量,称为边缘距离,边缘距离越大,两类样本分得越开,SVM就是寻找最大边缘距离的超平面,这个可以通过求解一个以超平面参数为求解变量的优化问题获得解决。给定适当的约束条件,这是一个二次优化问题,可以通过用KKT条件求解对偶问题等方法进行求解。
对于不是线性可分的问题,就不能通过寻找最优分类超平面进行分类,SVM这时通过把n维空间的样本映射到更高维的空间中,使得在高维的空间上样本是线性可分的。在实际的算法中,SVM不需要真正地进行样本点的映射,因为算法中涉及到的高维空间的计算总是以内积的形式出现,而高维空间的内积可以通过在原本n维空间中求内积然后再进行一个变换得到,这里计算两个向量在隐式地映射到高维空间的内积的函数就叫做核函数。SVM根据问题性质和数据规模的不同可以选择不同的核函数。
虽然SVM本质上是二分类的分类器,但是可以扩展成多分类的分类器,常见的方法有一对多(one-versus-rest)和一对一(one-versus-one)。在一对多方法中,训练时依次把k类样本中的某个类别归为一类,其它剩下的归为另一类,使用二分类的SVM训练处一个二分类器,最后把得到的k个二分类器组成k分类器。对未知样本分类时,分别用这k个二分类器进行分类,将分类结果中出现最多的那个类别作为最终的分类结果。而一对一方法中,训练时对于任意两类样本都会训练一个二分类器,最终得到k*(k-1)/2个二分类器,共同组成k分类器。对未知样本分类时,使用所有的k*(k-1)/2个分类器进行分类,将出现最多的那个类别作为该样本最终的分类结果。
LIBSVM中的多分类就是根据一对一的方法实现的。
四 使用
关于LIBSVM在Matlab中的使用,可以参看软件包中matlab目录下的README文件,这里对里面内容做一个翻译和一些细节的讲解。
1. 训练
libsvm函数用于对训练集的数据进行训练,得到训练好的模型。
model = libsvmtrain(training_label_vector, training_instance_matrix [, 'libsvm_options']);
这个函数有三个参数,其中
- -training_label_vector:训练样本的类标,如果有m个样本,就是m x 1的矩阵(类型必须为double)。这里可以是二分类和多分类,类标是(-1,1)、(1,2,3)或者其他任意用来表示不同的类别的数字,要转成double类型。
- -training_instance_matrix:训练样本的特征,如果有m个样本,每个样本特征是n维,则为m x n的矩阵(类型必须为double)。
- -libsvm_options:训练的参数,在第3点详细介绍。
2. 预测
libpredict函数用于对测试集的数据进行测试,还能对未知样本进行预测。
[predicted_label, accuracy, decision_values/prob_estimates]
= libsvmpredict(testing_label_vector, testing_instance_matrix, model [, 'libsvm_options']);
这个函数包括四个参数,其中
- -testing_label_vector:测试样本的类标,如果有m个样本,就是m x 1的矩阵(类型必须为double)。如果类标未知,可以初始化为任意m x 1的double数组。
- -testing_instance_matrix:测试样本的特征,如果有m个样本,每个样本特征是n维,则为m x n的矩阵(类型必须为double)。
- -model:使用libsvmtrain返回的模型
- -libsvm_options:预测的参数,与训练的参数形式一样。
3. 训练的参数
LIBSVM训练时可以选择的参数很多,包括:
- -s svm类型:SVM设置类型(默认0)
0 — C-SVC; 1 –v-SVC; 2 – 一类SVM; 3 — e-SVR; 4 — v-SVR - -t 核函数类型:核函数设置类型(默认2)
0 – 线性核函数:u’v
1 – 多项式核函数:(r*u’v + coef0)^degree
2 – RBF(径向基)核函数:exp(-r|u-v|^2)
3 – sigmoid核函数:tanh(r*u’v + coef0) - -d degree:核函数中的degree设置(针对多项式核函数)(默认3)
- -g r(gamma):核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数)(默认1/k,k为总类别数)
- -r coef0:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)
- -c cost:设置C-SVC,e -SVR和v-SVR的参数(损失函数)(默认1)
- -n nu:设置v-SVC,一类SVM和v- SVR的参数(默认0.5)
- -p p:设置e -SVR 中损失函数p的值(默认0.1)
- -m cachesize:设置cache内存大小,以MB为单位(默认40)
- -e eps:设置允许的终止判据(默认0.001)
- -h shrinking:是否使用启发式,0或1(默认1)
- -wi weight:设置第几类的参数C为weight*C (C-SVC中的C) (默认1)
- -v n: n-fold交互检验模式,n为fold的个数,必须大于等于2
以上这些参数设置可以按照SVM的类型和核函数所支持的参数进行任意组合,如果设置的参数在函数或SVM类型中没有也不会产生影响,程序不会接受该参数;如果应有的参数设置不正确,参数将采用默认值。
4. 训练返回的内容
libsvmtrain函数返回训练好的SVM分类器模型,可以用来对未知的样本进行预测。这个模型是一个结构体,包含以下成员:
- -Parameters: 一个5 x 1的矩阵,从上到下依次表示:
-s SVM类型(默认0);
-t 核函数类型(默认2)
-d 核函数中的degree设置(针对多项式核函数)(默认3);
-g 核函数中的r(gamma)函数设置(针对多项式/rbf/sigmoid核函数) (默认类别数目的倒数);
-r 核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0) - -nr_class: 表示数据集中有多少类别,比如二分类时这个值即为2。
- -totalSV: 表示支持向量的总数。
- -rho: 决策函数wx+b中的常数项的相反数(-b)。
- -Label: 表示数据集中类别的标签,比如二分类常见的1和-1。
- -ProbA: 使用-b参数时用于概率估计的数值,否则为空。
- -ProbB: 使用-b参数时用于概率估计的数值,否则为空。
- -nSV: 表示每类样本的支持向量的数目,和Label的类别标签对应。如Label=[1; -1],nSV=[63; 67],则标签为1的样本有63个支持向量,标签为-1的有67个。
- -sv_coef: 表示每个支持向量在决策函数中的系数。
- -SVs: 表示所有的支持向量,如果特征是n维的,支持向量一共有m个,则为m x n的稀疏矩阵。
另外,如果在训练中使用了-v参数进行交叉验证时,返回的不是一个模型,而是交叉验证的分类的正确率或者回归的均方根误差。
5. 预测返回的内容
libsvmtrain函数有三个返回值,不需要的值在Matlab可以用~进行代替。
- -predicted_label:第一个返回值,表示样本的预测类标号。
- -accuracy:第二个返回值,一个3 x 1的数组,表示分类的正确率、回归的均方根误差、回归的平方相关系数。
- -decision_values/prob_estimates:第三个返回值,一个矩阵包含决策的值或者概率估计。对于n个预测样本、k类的问题,如果指定“-b 1”参数,则n x k的矩阵,每一行表示这个样本分别属于每一个类别的概率;如果没有指定“-b 1”参数,则为n x k*(k-1)/2的矩阵,每一行表示k(k-1)/2个二分类SVM的预测结果。
6. 读取或保存
libsvmread函数可以读取以LIBSVM格式存储的数据文件。
[label_vector, instance_matrix] = libsvmread(‘data.txt’);
这个函数输入的是文件的名字,输出为样本的类标和对应的特征。
libsvmwrite函数可以把Matlab的矩阵存储称为LIBSVM格式的文件。
libsvmwrite(‘data.txt’, label_vector, instance_matrix]
这个函数有三个输入,分别为保存的文件名、样本的类标和对应的特征(必须为double类型的稀疏矩阵)。
五 更新:svdd扩展安装(2014.10)
从libsvm官网下载svdd工具箱,目前使用libsvm3.18以及svdd3.18版本。
- svdd工具箱里面有一个matlab文件夹和3个文件svm.cpp、svm.h、svm-train.c。
- 将matlab文件夹中的文件svmtrain.c覆盖原libsvm的matlab文件夹中的文件。
- 将svm.cpp、svm.h、svm-train.c这3个文件覆盖libsvm文件夹下的相同文件。
- 按本文刚开始讲述的方法进行mex -setup、make等完成安装,根据需要进行改名以及添加Path。
备注:
(1) libsvmread主要用于读取数据
这里的数据是非matlab下的.mat数据,比如说是.txt,.data等等,这个时候需要使用libsvmread函数进行转化为matlab可识别数据,比如自带的数据是heart_scale数据,那么导入到matlab有两种方式,
一种使用libsvmread函数,在matlab下直接libsvmread(heart_scale);
第二种方式为点击matlab的‘导入数据’按钮,然后导向heart_scale所在位置,直接选择就可以了。因为有的数据libsvmread读取不管用,但是‘导入数据’后就可以变成matlab下数据。
(2)libsvmwrite写函数,就是把已知数据存起来
使用方式为:libsvmwrite(‘filename’,label_vector, instance_matrix);
label_vector是标签,instance_matrix为数据矩阵(注意这个数据必须是稀疏矩阵,就是里面的数据不包含没用的数据(比如很多0),有这样的数据应该去掉再存)。
(3)svmtrain训练函数,训练数据产生模型的
一般直接使用为:model=svmtrain(label,data,cmd); label为标签,data为训练数据(数据有讲究,每一行为一个样本的所有数据,列数代表的是样本的个数),每一个样本都要对应一个标签(分类问题的话一般为二分类问题,也就是每一个样本对应一个标签)。
cmd为相应的命令集合,都有哪些命令呢?很多,-v,-t,-g,-c,等等,不同的参数代表的含义不同,
比如对于分类问题,这里-t就表示选择的核函数类型,-t=0时线性核。-t=1多项式核,-t=2,径向基函数(高斯),-t=3,sigmod核函数,新版出了个-t=4,预计算核(还不会用);
-g为核函数的参数系数,-c为惩罚因子系数,-v为交叉验证的数,默认为5,这个参数在svmtrain写出来使用与不写出来不使用的时候,model出来的东西不一样,不写的时候,model为一个结构体,是一个模型,可以带到svmpredict中直接使用,写出来的时候,出来的是一个训练模型的准确率,为一个数值。
用法: svmtrain [options] training_set_file [model_file]
其中, options为操作参数, 可用的选项即表示的涵义如下所示:
-s 设置svm类型:
0 – C-SVC
1 – v-SVC
2 – one-class-SVM
3 – ε-SVR
4 – n – SVR
-t 设置核函数类型, 默认值为2
0 — 线性核: μ‘∗ν
1 — 多项式核: (γ∗μ‘∗ν+coef0)degree
2 — RBF核: exp(–γ∗∥μ−ν∥2)
3 — sigmoid 核: tanh(γ∗μ‘∗ν+coef0)
-d degree: 核函数中的degree设置(针对多项式核函数)(默认3);
-g r(gama): 核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数)(默认1/ k);
-r coef0: 核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0);
-c cost: 设置C-SVC, e -SVR和v-SVR的参数(损失函数)(默认1);
-n nu: 设置v-SVC, 一类SVM和v- SVR的参数(默认0.5);
-p p: 设置e -SVR 中损失函数p的值(默认0.1);
-m cachesize: 设置cache内存大小, 以MB为单位(默认40);
-e eps: 设置允许的终止判据(默认0.001);
-h shrinking: 是否使用启发式, 0或1(默认1);
-wi weight: 设置第几类的参数C为weight*C (C-SVC中的C) (默认1);
-v n: n-fold交互检验模式, n为fold的个数, 必须大于等于2;
-b 概率估计: 是否计算SVC或SVR的概率估计, 可选值0或1, 默认0;
model_file: 可选项, 为要保存的结果文件, 称为模型文件, 以便在预测时使用.- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
(3)svmpredict训练函数,使用训练的模型去预测来的数据类型。
使用方式为:
[predicted_label,accuracy,decision_values/prob_estimates]= svmpredict(testing_label_vector,testing_instance_matrix,model,’libsvm_options’) - 1
- 1
或者:
[predicted_label]=svmpredict(testing_label_vector,testing_instance_matrix, model, ‘libsvm_options’) - 1
- 1
第一种方式中,输出为三个参数,预测的类型,准确率,评估值(非分类问题用着),输入为测试类型(这个可与可无,如果没有,那么预测的准确率accuracy就没有意义了,如果有,那么就可以通过这个值与预测出来的那个类型值相比较得出准确率accuracy,但是要说明一点的是,无论这个值有没有,在使用的时候都得加上,即使没有,也要随便加上一个类型值,反正你也不管它对不对,这是函数使用所规定的的),再就是输入数据值,最后是参数值(这里的参数值只有两种选择,-p和-b参数),曾经遇到一个这样的问题,比如说我在训练函数中规定了-g参数为0.1,那么在预测的时候是不是也要规定这个参数呢?当你规定了以后,程序反而错误,提醒没有svmpredict的-g参数,原因是在svmtrain后会出现一个model,而在svmpredict中你已经用了这个model,而这个model中就已经包含了你所有的训练参数了,所以svmpredict中没有这个参数,那么对于的libsvm_options就是-p和-b参数了。对于函数的输出,两种方式调用的方法不一样,第一种调用把所有需要的数据都调用出来了,二第二种调用,只调用了predicted_label预测的类型,这里我们可以看到,在单纯的分类预测模型中,其实第二种方式更好一些吧,既简单有实用。
下面给出一个在Matlab中运行SVM的示例
https://sites.google.com/site/kittipat/libsvm_matlab
本文转自:
http://blog.csdn.net/abcjennifer/article/details/7370177
http://blog.csdn.net/on2way/article/details/47733861
http://blog.csdn.net/m624197265/article/details/41894261
https://sites.google.com/site/kittipat/libsvm_matlab
关于SVM参数c&g选取的总结(matlab-libsvm)
选取SVM中参数 c和g的最佳值
寻找最佳c和g的思想仍然是让c和g在一定的范围里跑(比如 c = 2^(-5),2^(-4),…,2^(5),g = 2^(-5),2^(-4),…,2^(5)),然后用cross validation的想法找到是的准确率最高的c和g,在这里做了一点修改是: 因为会有不同的c和g都对应最高的的准确率,我把具有最小c的那组c和g认为是最佳的c和g,因为惩罚参数不能设置 太高,很高的惩罚参数能使得validation数据的准确率提高,但过高的惩罚参数c会造成过学习状态,往往都是惩罚参数c过高会导致最终测试集合的准确率并不是很理想 。
先大范围粗糙的找 比较理想的c和g,然后再细范围找更加理想的c和g.
比如首先让 c = 2^(-5),2^(-4),…,2^(5),g = 2^(-5),2^(-4),…,2^(5)在这个范围找比较理想的c和g。
此时bestc = 0.5,bestg=1,bestacc = 98.8764[cross validation 的准确率]
最终测试集合的准确率 Accuracy = 96.6292% (86/89) (classification)
示例
load wine_SVM;
train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)];
train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)];
test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)];
test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)];
[train_wine,pstrain] = mapminmax(train_wine');
pstrain.ymin = 0;
pstrain.ymax = 1;
[train_wine,pstrain] = mapminmax(train_wine,pstrain);
[test_wine,pstest] = mapminmax(test_wine');
pstest.ymin = 0;
pstest.ymax = 1;
[test_wine,pstest] = mapminmax(test_wine,pstest);
train_wine = train_wine';
test_wine = test_wine';
[bestacc,bestc,bestg] = SVMcg(train_wine_labels,train_wine,-2,4,-4,4,3,0.5,0.5,0.9);
cmd = ['-c ',num2str(bestc),' -g ',num2str(bestg)];
model = svmtrain(train_wine_labels,train_wine,cmd);
[pre,acc] = svmpredict(test_wine_labels,test_wine,model);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
function [bestacc,bestc,bestg] = SVMcg(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,accstep)
%SVMcg cross validation by faruto
%Email:[email protected] QQ:516667408 http://blog.sina.com.cn/faruto BNU
%last modified 2009.8.23
%Super Moderator @ www.ilovematlab.cn
% 使用说明.如下:
% [bestacc,bestc,bestg] = SVMcg(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,accstep)
%
% train_label:训练 集标签.要求与libsvm工具箱中要求一致.
% train:训练集.要求与libsvm工具箱中要求一致.
% cmin:惩罚参数c的变化范围的最小值(取以2为底的对数后),即 c_min = 2^(cmin).默认为 -5
% cmax:惩罚参数c的变化范围的最大值(取以2为底的对数后),即 c_max = 2^(cmax).默认为 5
% gmin:参数g的变化范围的最小值(取以2为底的对数后),即 g_min = 2^(gmin).默认为 -5
% gmax:参数g的变化范围的最小值(取以2为底的对数后),即 g_min = 2^(gmax).默认为 5
%
% v:cross validation的参数,即给测试集分为几部分进行cross validation.默认为 3
% cstep:参数c步进的大小.默认为 1
% gstep:参数g步进的大小.默认为 1
% accstep:最后显示准确率图时的步进大小. 默认为 1.5
%% about the parameters of SVMcg
if nargin < 10
accstep = 1.5;
end
if nargin < 8
accstep = 1.5;
cstep = 1;
gstep = 1;
end
if nargin < 7
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
end
if nargin < 6
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
end
if nargin < 5
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
gmin = -5;
end
if nargin < 4
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
gmin = -5;
cmax = 5;
end
if nargin < 3
accstep = 1.5;
v = 3;
cstep = 1;
gstep = 1;
gmax = 5;
gmin = -5;
cmax = 5;
cmin = -5;
end
%% X:c Y:g cg:acc
[X,Y] = meshgrid(cmin:cstep:cmax,gmin:gstep:gmax);
[m,n] = size(X);
cg = zeros(m,n);
%% record acc with different c & g,and find the bestacc with the smallest c
bestc = 0;
bestg = 0;
bestacc = 0;
basenum = 2;
for i = 1:m
for j = 1:n
cmd = ['-v ',num2str(v),' -c ',num2str( basenum^X(i,j) ),' -g ',num2str( basenum^Y(i,j) )];
cg(i,j) = svmtrain(train_label, train, cmd);
if cg(i,j) > bestacc
bestacc = cg(i,j);
bestc = basenum^X(i,j);
bestg = basenum^Y(i,j);
end
if ( cg(i,j) == bestacc && bestc > basenum^X(i,j) )
bestacc = cg(i,j);
bestc = basenum^X(i,j);
bestg = basenum^Y(i,j);
end
end
end
%% to draw the acc with different c & g
[C,h] = contour(X,Y,cg,60:accstep:100);
clabel(C,h,'FontSize',10,'Color','r');
xlabel('log2c','FontSize',10);
ylabel('log2g','FontSize',10);
grid on;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
具体详情请查看
http://blog.csdn.net/alextowarson/article/details/4764801