A-Eddy Walker
题目链接：https://ac.nowcoder.com/acm/contest/882/A
数论队友：https://blog.csdn.net/henucm/article/details/97111654
B-Eddy Walker2
题目链接：https://blog.csdn.net/henucm/article/details/99566371
数论队友：https://blog.csdn.net/henucm/article/details/99566371
D-Kth Minimum Clique
题目链接：https://ac.nowcoder.com/acm/contest/882/D
题目大意：给出一个n个顶点的无向加权图，求第k个最小加权群。两个不同的顶点相邻时，顶点的子集称之为团()
思路：bitset优化暴力求和。将每个点的相邻点用bitset表示，然后暴力求团。由于求的是第k小，所以我们将最小的求出来，依次加边，维护优先队列，直到第k小的团为止。注意一点，新加入的点必须能和之前的点都联通(子集)。同时为了保证不会重复加点，我们都从最后一个点开始加。
ACcode：
#include
#include
#include
#include
#include
// srand(unsigned)time(NULL));rand();
#include
E-MAZE
题目链接：https://ac.nowcoder.com/acm/contest/882/E
文少DP+线段树：https://blog.csdn.net/henu_1710252529/article/details/102637240
F-Partition problem
题目链接：https://ac.nowcoder.com/acm/contest/882/F
题目大意：2n个人，分成红队或白队，每个队n人，使得竞争价值最大化。竞争价值是不同对中没对人的竞争价值之和。（任意两人之间的竞争价值之和）。给出一个邻接矩阵，表示的是i，j之间的竞争价值。
思路：枚举第一队的人，刷新竞争价值之和。二进制每一位表示该位置的人是否在1队。然后更新价值。一个二进制枚举题目，n并不大。
ACCode：
#include
#include
#include
#include
#include
// srand(unsigned)time(NULL));rand();
#include
G-Polygons
题目链接：https://ac.nowcoder.com/acm/contest/882/G
题目大意：给出n条直线，找出这n条直线，判断能够围成的多边形的数量，输出最大最小值，并输出前q个第qi大小的多边形面积。没有输出Invalid question
思路：我们用图的方法解决这道题。将所有的直线之间两两交点做成无向图。遍历每个点，每次找夹角最小的边，然后回归原点后，即可求出所求面积。
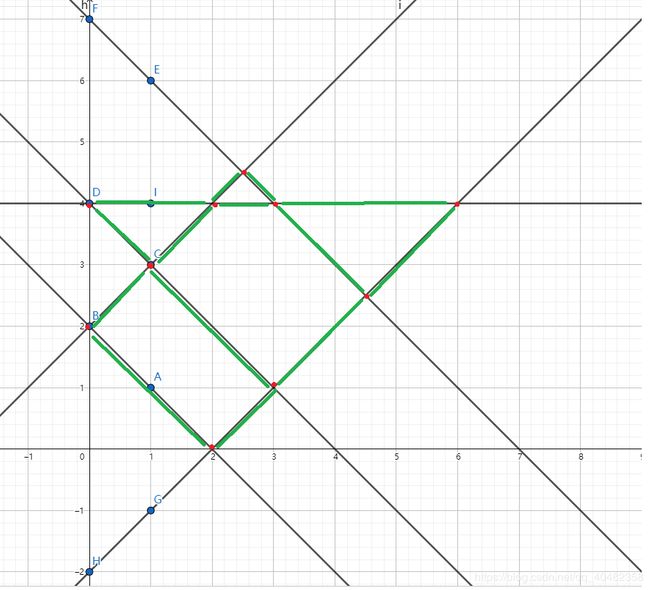如图所示，红点表示的是线线之间的交点，绿线表示双向边。
枚举交点，找到最小回路。走完后删掉这条边(边权置为0）。
ACCode：
#include
#include
#include
#include
#include
// srand((unsigned)time(NULL));rand();
#include
H-Second Large Rectangle
题目链接：https://ac.nowcoder.com/acm/contest/882/H
题目大意：给出一个n*m的01矩阵，找出第二小的全1矩阵。
思路：二维单调栈，枚举每一行，维护一个单增栈，每次记录大小。
ACCode：
#include
#include
#include
#include
#include
// srand(unsigned)time(NULL));rand();
#include
J-Subarray
题目链接：https://ac.nowcoder.com/acm/contest/882/J
题目大意：有一个1e9长度的全-1数组，现在里面有不超过1e7个1，求有多少个区间数量，区间内之和>0的。
思路：很迷，感觉好难，需要再研究研究。
ACCode：
#include
#include
#include
#include
#include
// srand((unsigned)time(NULL));rand();
#include
