2019牛客多校训练营第三场H.Magic Line

2019牛客多校训练营第三场 H.Magic Line

题目链接

题目描述

There are always some problems that seem simple but is difficult to solve.

$ZYB$ got $N$ distinct points on a two-dimensional plane. He wants to draw a magic line so that the points will be divided into two parts, and the number of points in each part is the same. There is also a restriction: this line can not pass through any of the points.

Help him draw this magic line.

输入描述

There are multiple cases. The first line of the input contains a single integer $T$ ($1\le T\le 10000$) indicating the number of cases.

For each case, the first line of the input contains a single even integer $N$ ($2\le N\le 1000$), the number of points. The following $N$ lines each contains two integers $x_i,y_i$ ($\mid x_i,y_i\mid \le 1000$), denoting the $x$-coordinate and the $y$-coordinate of the $i$-th point.

It is guaranteed that the sum of $N$ over all cases does not exceed $2\times 10^5$.

题目大意

在笛卡尔坐标系中有$N$个点，去找到某一条直线将这$N$个点划分为两个部分，每个部分点的个数相同，同时该直线不能经过坐标系中任意一个点，找到该直线中的两个整数点。

解题思路

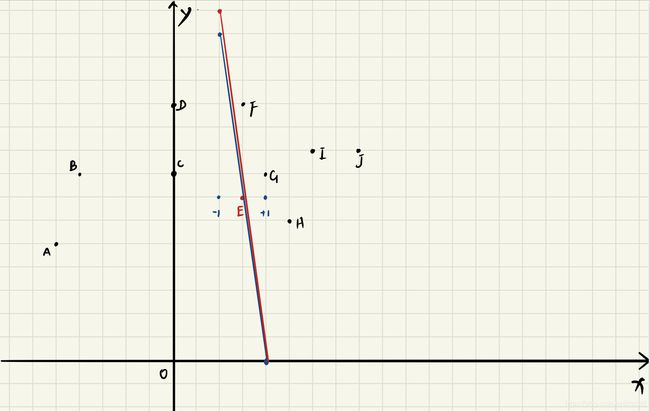
坐标系中的每个点按照$x$从小到大排序，若$x$相同则按照$y$从小到大进行排序，找到中间点$(x,y)$，过中间点垂直于$x$轴的直线$l$能够将坐标系中的点划分为近似相等的两个部分，由中间点坐标可以得到两个点，$a(x-1,y+10^8)$，$b(x+1,y-10^8)$，（至于为什么加$10^8$，因为必须要加一个特别大的数才能让垂直的直线变化尽可能的小，而题目中告诉$max(x_i)，max(y_i)$为$1000$，而最后答案不能超过$10^9$，能加的最大数即为$10^8$）过这两点的直线得到过中点$(x,y)$且近似为$l$的一条直线，然后$a$点的$y$坐标+1，将直线稍微向上倾斜，点E划分到左边部分，由此得到的直线可以将坐标系中的点划分为两个部分。

AC代码

#include 
const int Max_N=1e3+100;
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
struct Num
{
    int x,y;
};
bool cmp(Num a,Num b)
{
    if(a.x!=b.x)
        return a.x<b.x;
    return a.y<b.y;
}
Num num[Max_N];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        for(int i=0;i<n;i++)
        {
            cin>>num[i].x>>num[i].y;
        }
        sort(num,num+n,cmp);
        ll x1=num[n/2-1].x;
        ll y1=num[n/2-1].y;
        cout<<x1-1<<" "<<(ll)(y1+100000000+1)<<" "<<x1+1<<" "<<(ll)(y1-100000000)<<endl;
    }
    return 0;
}

总结

在最开始的时候把这道题想的太复杂了，由此陷入了思维泥潭。该题虽然是在二维坐标中，但在划分为两个部分的时候思路只需考虑一维的情况，然后稍微扩展一点便可。