- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
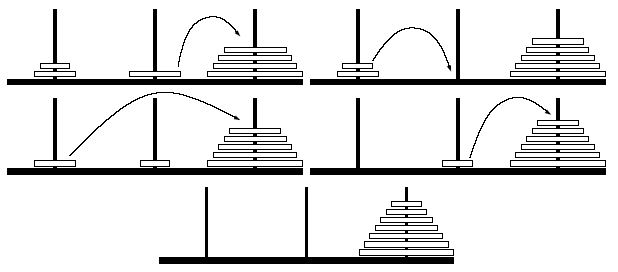
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- 代码随想录Day 41|动态规划之买卖股票问题,leetcode题目121. 买卖股票的最佳时机、122. 买卖股票的最佳时机Ⅱ、123. 买卖股票的最佳时机Ⅲ
LluckyYH
动态规划leetcode算法数据结构
提示:DDU,供自己复习使用。欢迎大家前来讨论~文章目录买卖股票的最佳时机相关题目题目一:121.买卖股票的最佳时机解题思路:题目二:122.买卖股票的最佳时机II解题思路:题目三:123.买卖股票的最佳时机III解题思路总结买卖股票的最佳时机相关题目题目一:121.买卖股票的最佳时机[[121.买卖股票的最佳时机](https://leetcode.cn/problems/combination
- 后端开发刷题 | 把数字翻译成字符串(动态规划)
jingling555
笔试题目动态规划java算法数据结构后端
描述有一种将字母编码成数字的方式:'a'->1,'b->2',...,'z->26'。现在给一串数字,返回有多少种可能的译码结果数据范围:字符串长度满足0=10&&num<=26){if(i==1){dp[i]+=1;}else{dp[i]+=dp[i-2];}}}returndp[nums.length()-1];}}
- 滑动窗口+动态规划
wniuniu_
算法动态规划算法
前言:分析这个题目的时候,就知道要这两个线段要分开,但是要保证得到最优解,那么我们在选取第二根线段的时候,要保证我们第一根线段是左边最优解并且我们选的两根线段的右端点一定是我们的数组的点(贪心思想)classSolution{public:intmaximizeWin(vector&prizePositions,intk){intn=prizePositions.size();vectormx(n
- 【NO.72】LeetCode HOT 100—279. 完全平方数
悬浮海
#LeetCodeHOT100leetcode算法279.完全平方数
文章目录279.完全平方数解题方法:动态规划279.完全平方数给你一个整数n,返回和为n的完全平方数的最少数量。完全平方数是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9和16都是完全平方数,而3和11不是。示例1:输入:n=12输出:3解释:12=4+4+4示例2:输入:n=13输出:2解释:13=4+9提示:1<=n<=104解题方法:动态规划动态规划
- 洛谷P2066 机器分配
summ1ts
算法动态规划
此题可用动态规划解决,首先进行阶段划分,可将解决问题的过程看作逐一为每家公司分配机器,因此按照已分配公司数量划分阶段,设变量i代表前i家公司。设计状态,设f[i][j]代表前i家公司分配j台设备能产生的最大盈利。确定决策为第i家公司分配多少设备,决策变量k范围0usingnamespacestd;inta[20][20],f[20][20],g[20][20];intn,m;voidprint(i
- 代码随想录算法训练营第46天 | LeetCode647.回文子串、 LeetCode516.最长回文子序列
霸L
算法数据结构动态规划
目录LeetCode647.回文子串1.动态规划2.双指针法LeetCode516.最长回文子序列LeetCode647.回文子串给你一个字符串s,请你统计并返回这个字符串中回文子串的数目。回文字符串是正着读和倒过来读一样的字符串。子字符串是字符串中的由连续字符组成的一个序列。思路:在回溯系列也做过求给定字符串的所有回文子串,那里求的是所有的划分结果,这里统计的是回文子串的数目,但是因为回溯本质上
- 12312312
二进制掌控者
c++
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c++,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm=1001.2014.3001.5343给大家分享一句我很喜欢我话:知不足而奋进,望远山而前行!!!铁铁们,成功的路上必然是孤独且艰难的,但是我们不可以放弃,远山就在前方,但我们
- 你知道什么是回调函数吗?
二进制掌控者
#C语言专栏c语言开发语言
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c++,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm=1001.2014.3001.5343给大家分享一句我很喜欢我话:知不足而奋进,望远山而前行!!!铁铁们,成功的路上必然是孤独且艰难的,但是我们不可以放弃,远山就在前方,但我们
- Leetcode面试经典150题-221.最大正方形
鱼跃鹰飞
数据结构与算法字节跳动高频面试题leetcode面试算法
解法都在代码里,不懂就留言或者私信classSolution{/**本题一看就是典型的动态规划,要找以每个点为右下角的正方形的面积,然后取最大的这个题要注意找规律,我找到的规律如下:1.以第一行为右下角的,因为正方形是边长相同的,所以第一行为右下角最大正方形只能是自己,自己是1就是1,不是1就是02.以第一列为右下角的也是一样。3.以普通位置为右下角的最大正方形,首先看自己是不是1,如果自己不是1
- 【NO.5】LeetCode HOT 100—5. 最长回文子串
悬浮海
#LeetCodeHOT100leetcode算法5.最长回文子串
文章目录5.最长回文子串解题方法一:动态规划方法二:中心扩展5.最长回文子串5.最长回文子串给你一个字符串s,找到s中最长的回文子串。如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。示例1:输入:s=“babad”输出:“bab”解释:“aba”同样是符合题意的答案。示例2:输入:s=“cbbd”输出:“bb”提示:1maxLength){maxLength=j-i+1;index=i
- 大二上学期详细学习计划
学会沉淀。
学习
本学习完成目标:项目:书籍:《mysql必知必会》《java核心技术卷》(暂时)加强JavaSE的学习,掌握Java核心Mysql+sql(把牛客上的那50道sql语句题写完)git+maven完成springboot项目(跟着黑马敲)对于每天的Java学习进行记录算法:刷题(多去刷cf上的题,每周15道)针对最近比赛薄弱的地方加强练习(图论,字符串,动态规划,搜索)cf先上1400,牛客和atc
- 代码随想录算法训练营第三十九天| 62. 不同路径,63. 不同路径 II
零offer在手
算法动态规划图论
62.不同路径搞清楚dp[i][j]的定义推导出公式遍历顺序,从左到右,从上到下dp的初始化动态规划中如何初始化很重要!|LeetCode:62.不同路径_哔哩哔哩_bilibili《代码随想录》算法公开课开讲啦!快来打卡!本期视频的文字讲解版在「代码随想录」刷题网站:programmercarl.comGithub:https://github.com/youngyangyang04/leetc
- 数学建模笔记——动态规划
liangbm3
数学建模笔记数学建模笔记动态规划python背包问题算法优化问题
数学建模笔记——动态规划动态规划1.模型原理2.典型例题2.1例1凑硬币2.2例2背包问题3.python代码实现3.1例13.2例2动态规划1.模型原理动态规划是运筹学的一个分支,通常用来解决多阶段决策过程最优化问题。动态规划的基本想法就是将原问题转换为一系列相互联系的子问题,然后通过逐层地推来求得最后的解。目前,动态规划常常出现在各类计算机算法竞赛或者程序员笔试面试中,在数学建模中出现的相对较
- 代码随想录训练营 Day38打卡 动态规划 part06 322. 零钱兑换 279. 完全平方数 139. 单词拆分
那一抹阳光多灿烂
力扣动态规划动态规划算法python力扣
代码随想录训练营Day38打卡动态规划part06一、力扣322.零钱兑换给你一个整数数组coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回-1。你可以认为每种硬币的数量是无限的。示例:输入:coins=[1,2,5],amount=11输出:3解释:11=5+5+1题目中说每种硬币的数量是
- 代码随想录训练营 Day45打卡 动态规划 part12 115. 不同的子序列 583. 两个字符串的删除操作 72. 编辑距离
那一抹阳光多灿烂
力扣动态规划动态规划算法leetcodepython
代码随想录训练营Day45打卡动态规划part12一、力扣115.不同的子序列给你两个字符串s和t,统计并返回在s的子序列中t出现的个数,结果需要对109+7取模。示例:输入:s=“rabbbit”,t=“rabbit”输出:3解释:如下所示,有3种可以从s中得到“rabbit”的方案。rabbbitrabbbitrabbbit确定dp数组的定义dp[i][j]表示s的前i个字符中子序列等于t的前
- 算法设计与分析期末复习题汇总
wisdom_zhe
Java题库算法
文章目录1、选择题1.1选择题11.2选择题22、判断题2.1判断题12.2判断题23、填空题3.1算法填空3.2填空题24、简答题1、选择题1.1选择题11、下列不是动态规划算法基本步骤的是(A)。A、找出最优解的解空间B、构造最优解C、算出最优解D、定义最优解2、最大效益优先是(A)的一搜索方式。A、分支界限法B、动态规划法C、贪心法D、回溯法3、最长公共子序列算法利用的算法是(B)。A、分支
- 五一的成果
王跃坤txdy
emm。。五一过了有意义的四天。原来简单的图论我也是可以搞出来的原来DFS放进图论真的会使难度变大原来BFS在没有出口的时候会以超指数的爆炸增长原来二叉树并不是很难原来哈希的速度远超数组原来动态规划滚动起来速度真的快原来栈是那么的有用,可惜来不及学了(遇到一个求化学方程式的算法题,我自己写了133行的字符串处理,原来用栈可以缩减3倍的代码)原来很多复杂的问题都可以拆解成很简单的问题比如我好像发现数
- [01] 动态规划解题套路框架
_魔佃_
本文解决几个问题:动态规划是什么?解决动态规划问题有什么技巧?如何学习动态规划?刷题刷多了就会发现,算法技巧就那几个套路。所以本文放在第一章,来扒一扒动态规划的裤子,形成一套解决这类问题的思维框架,希望能够成为解决动态规划问题的一部指导方针。本文就来讲解该算法的基本套路框架,下面上干货。labuladong的算法小抄首先,动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法,只不
- 【动态规划【hard】力扣1449. 数位成本和为目标值的最大数字
sjsjs11
动态规划动态规划leetcode算法
给你一个整数数组cost和一个整数target。请你返回满足如下规则可以得到的最大整数:给当前结果添加一个数位(i+1)的成本为cost[i](cost数组下标从0开始)。总成本必须恰好等于target。添加的数位中没有数字0。由于答案可能会很大,请你以字符串形式返回。如果按照上述要求无法得到任何整数,请你返回“0”。示例1:输入:cost=[4,3,2,5,6,7,2,5,5],target=9
- 【每日一题】LeetCode 2708.一个小组的最大实力值(一次遍历、分类讨论、动态规划)
Chase-Hart
算法leetcode动态规划算法数据结构java
【每日一题】LeetCode2708.最大实力值小组(一次遍历、分类讨论、动态规划)题目描述给定一个整数数组nums,表示一个班级中所有学生在一次考试中的成绩。老师想从这个班级中选出一部分同学组成一个非空小组,使得这个小组的实力值最大。小组的实力值定义为小组中所有学生成绩的乘积。请返回老师创建的小组能得到的最大实力值。思路分析这个问题可以通过动态规划的思想来解决。我们需要维护两个变量,mn和mx,
- Java数据结构与算法:动态规划之斐波那契数列
省赚客APP开发者@聚娃科技
java动态规划代理模式
Java数据结构与算法:动态规划之斐波那契数列大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编。在这寒冷的季节里,让我们一同探讨Java中的动态规划,重点关注解决问题的经典代表之一——斐波那契数列。动态规划简介动态规划是一种解决问题的数学方法,通常用于优化递归算法。它通过将问题分解为子问题并保存它们的解,避免重复计算,从而提高算法效率。在动态规划的应用中,最常见的问题之一就是求
- 动态规划算法之最长公子序列详细解读(附带Java代码解读)
南城花随雪。
算法分析算法动态规划java
最长公共子序列(LongestCommonSubsequence,LCS)问题是动态规划中另一个经典问题,广泛用于比较两个序列的相似度。它的目标是找到两个序列之间最长的公共子序列(不是连续的),使得这个子序列同时出现在两个序列中。1.问题定义给定两个序列X和Y,要找到它们的最长公共子序列,即一个序列Z,它同时是X和Y的子序列,且Z的长度最大。例如:对于序列X="ABCBDAB"和Y="BDCAB"
- Leetcode:139. 单词拆分(C++)
Cosmoshhhyyy
LeetCodeleetcodec++算法动态规划
目录问题描述:实现代码与解析:动态规划(完全背包):原理思路:问题描述:给你一个字符串s和一个字符串列表wordDict作为字典。请你判断是否可以利用字典中出现的单词拼接出s。注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。示例1:输入:s="leetcode",wordDict=["leet","code"]输出:true解释:返回true因为"leetcode"可以由"l
- 力扣第213题“打家劫舍 II”
数据分析螺丝钉
LeetCode刷题与模拟面试面试算法leetcode经验分享python
在本篇文章中,我们将详细解读力扣第213题“打家劫舍II”。通过学习本篇文章,读者将掌握如何使用动态规划来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。问题描述力扣第213题“打家劫舍II”描述如下:你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这一整条街的所有房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的
- 动态规划算法之背包问题详细解读(附带Java代码解读)
南城花随雪。
算法分析算法动态规划
动态规划中的背包问题(KnapsackProblem)是经典问题之一,通常用来解决选择一组物品放入背包使得背包的价值最大化的问题。根据问题条件的不同,背包问题有很多种变体,如0-1背包问题、完全背包问题、多重背包问题等。这里,我们详细介绍最经典的0-1背包问题,并提供代码的详细解读。1.0-1背包问题简介在0-1背包问题中,有一个容量为C的背包和n件物品。每件物品有两个属性:重量w[i]和价值v[
- 代码随想录27期|Python|Day49|动态规划| 300. 最长递增子序列|674. 最长连续递增序列|718. 最长重复子数组
Lily_Mei
算法python
300.最长递增子序列本题是子序列一套的开始。1、确定dp数组的含义本题中,正确定义dp数组的含义十分重要。dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。2、确定初始化每一个数字都可以独立构成一个子序列,所以数组初始化全部为1.3、确定递推公式在本题的遍历过程中,由于序列构成子序列是不连续删除构成的,所以递推公式不能确定为由之前某一个状态直接推到而来,所以在递推的公式中,
- Leetcode刷题记录分享——数据结构(队列) #200 岛屿数量
三年买房不是梦
Leetcode数据结构leetcode数据结构队列bfs
Leetcode刷题记录分享——数据结构(队列)PS:刷题两周了,每周天会专门抽出一段时间来刷Leetcode,这学期在学算法设计与分析,根据课程内容,第一周刷动态规划题目,第二周刷的贪心算法。打算从这周开始刷数据结构。数据结构是大二上学期学的了,过去了一年,当时学的也不扎实,现在通过Leetcode理论+实践重新学习一下。我刷Leetcode会先看一下优质解答,肚里没货硬刚也刚不出来,主要是学习
- Floyd算法求最短路径
阿轩不熬夜~~
算法学习c++数据结构
目录一.Floyd算法介绍二.算法实现一.邻接矩阵介绍二.过程简述三.Floyd核心代码三.例题分析一.B3647【模板】Floyd.二.P2835刻录光盘四.Floyd算法的优缺点一.Floyd算法介绍Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教
- c++使用动态规划求解01背包问题
苓一在学习
算法c++
-什么是01背包问题?在01背包问题中,因为每种物品只有一个,对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中,则不需要处理。如果选择将其放入背包中,由于不清楚之前放入的物品占据了多大的空间,需要枚举将这个物品放入背包后可能占据背包空间的所有情况。需要注意的是:01背包问题不能使用贪心思想,因为每次选取最大的并不能保证背包刚好装满,遇到01背包问题先找到题目中的“背包”和“物品”,
- 项目中 枚举与注解的结合使用
飞翔的马甲
javaenumannotation
前言:版本兼容,一直是迭代开发头疼的事,最近新版本加上了支持新题型,如果新创建一份问卷包含了新题型,那旧版本客户端就不支持,如果新创建的问卷不包含新题型,那么新旧客户端都支持。这里面我们通过给问卷类型枚举增加自定义注解的方式完成。顺便巩固下枚举与注解。
一、枚举
1.在创建枚举类的时候,该类已继承java.lang.Enum类,所以自定义枚举类无法继承别的类,但可以实现接口。
- 【Scala十七】Scala核心十一:下划线_的用法
bit1129
scala
下划线_在Scala中广泛应用,_的基本含义是作为占位符使用。_在使用时是出问题非常多的地方,本文将不断完善_的使用场景以及所表达的含义
1. 在高阶函数中使用
scala> val list = List(-3,8,7,9)
list: List[Int] = List(-3, 8, 7, 9)
scala> list.filter(_ > 7)
r
- web缓存基础:术语、http报头和缓存策略
dalan_123
Web
对于很多人来说,去访问某一个站点,若是该站点能够提供智能化的内容缓存来提高用户体验,那么最终该站点的访问者将络绎不绝。缓存或者对之前的请求临时存储,是http协议实现中最核心的内容分发策略之一。分发路径中的组件均可以缓存内容来加速后续的请求,这是受控于对该内容所声明的缓存策略。接下来将讨web内容缓存策略的基本概念,具体包括如如何选择缓存策略以保证互联网范围内的缓存能够正确处理的您的内容,并谈论下
- crontab 问题
周凡杨
linuxcrontabunix
一: 0481-079 Reached a symbol that is not expected.
背景:
*/5 * * * * /usr/IBMIHS/rsync.sh
- 让tomcat支持2级域名共享session
g21121
session
tomcat默认情况下是不支持2级域名共享session的,所有有些情况下登陆后从主域名跳转到子域名会发生链接session不相同的情况,但是只需修改几处配置就可以了。
打开tomcat下conf下context.xml文件
找到Context标签,修改为如下内容
如果你的域名是www.test.com
<Context sessionCookiePath="/path&q
- web报表工具FineReport常用函数的用法总结(数学和三角函数)
老A不折腾
Webfinereport总结
ABS
ABS(number):返回指定数字的绝对值。绝对值是指没有正负符号的数值。
Number:需要求出绝对值的任意实数。
示例:
ABS(-1.5)等于1.5。
ABS(0)等于0。
ABS(2.5)等于2.5。
ACOS
ACOS(number):返回指定数值的反余弦值。反余弦值为一个角度,返回角度以弧度形式表示。
Number:需要返回角
- linux 启动java进程 sh文件
墙头上一根草
linuxshelljar
#!/bin/bash
#初始化服务器的进程PId变量
user_pid=0;
robot_pid=0;
loadlort_pid=0;
gateway_pid=0;
#########
#检查相关服务器是否启动成功
#说明:
#使用JDK自带的JPS命令及grep命令组合,准确查找pid
#jps 加 l 参数,表示显示java的完整包路径
#使用awk,分割出pid
- 我的spring学习笔记5-如何使用ApplicationContext替换BeanFactory
aijuans
Spring 3 系列
如何使用ApplicationContext替换BeanFactory?
package onlyfun.caterpillar.device;
import org.springframework.beans.factory.BeanFactory;
import org.springframework.beans.factory.xml.XmlBeanFactory;
import
- Linux 内存使用方法详细解析
annan211
linux内存Linux内存解析
来源 http://blog.jobbole.com/45748/
我是一名程序员,那么我在这里以一个程序员的角度来讲解Linux内存的使用。
一提到内存管理,我们头脑中闪出的两个概念,就是虚拟内存,与物理内存。这两个概念主要来自于linux内核的支持。
Linux在内存管理上份为两级,一级是线性区,类似于00c73000-00c88000,对应于虚拟内存,它实际上不占用
- 数据库的单表查询常用命令及使用方法(-)
百合不是茶
oracle函数单表查询
创建数据库;
--建表
create table bloguser(username varchar2(20),userage number(10),usersex char(2));
创建bloguser表,里面有三个字段
&nbs
- 多线程基础知识
bijian1013
java多线程threadjava多线程
一.进程和线程
进程就是一个在内存中独立运行的程序,有自己的地址空间。如正在运行的写字板程序就是一个进程。
“多任务”:指操作系统能同时运行多个进程(程序)。如WINDOWS系统可以同时运行写字板程序、画图程序、WORD、Eclipse等。
线程:是进程内部单一的一个顺序控制流。
线程和进程
a. 每个进程都有独立的
- fastjson简单使用实例
bijian1013
fastjson
一.简介
阿里巴巴fastjson是一个Java语言编写的高性能功能完善的JSON库。它采用一种“假定有序快速匹配”的算法,把JSON Parse的性能提升到极致,是目前Java语言中最快的JSON库;包括“序列化”和“反序列化”两部分,它具备如下特征:
- 【RPC框架Burlap】Spring集成Burlap
bit1129
spring
Burlap和Hessian同属于codehaus的RPC调用框架,但是Burlap已经几年不更新,所以Spring在4.0里已经将Burlap的支持置为Deprecated,所以在选择RPC框架时,不应该考虑Burlap了。
这篇文章还是记录下Burlap的用法吧,主要是复制粘贴了Hessian与Spring集成一文,【RPC框架Hessian四】Hessian与Spring集成
- 【Mahout一】基于Mahout 命令参数含义
bit1129
Mahout
1. mahout seqdirectory
$ mahout seqdirectory
--input (-i) input Path to job input directory(原始文本文件).
--output (-o) output The directory pathna
- linux使用flock文件锁解决脚本重复执行问题
ronin47
linux lock 重复执行
linux的crontab命令,可以定时执行操作,最小周期是每分钟执行一次。关于crontab实现每秒执行可参考我之前的文章《linux crontab 实现每秒执行》现在有个问题,如果设定了任务每分钟执行一次,但有可能一分钟内任务并没有执行完成,这时系统会再执行任务。导致两个相同的任务在执行。
例如:
<?
//
test
.php
- java-74-数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字
bylijinnan
java
public class OcuppyMoreThanHalf {
/**
* Q74 数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字
* two solutions:
* 1.O(n)
* see <beauty of coding>--每次删除两个不同的数字,不改变数组的特性
* 2.O(nlogn)
* 排序。中间
- linux 系统相关命令
candiio
linux
系统参数
cat /proc/cpuinfo cpu相关参数
cat /proc/meminfo 内存相关参数
cat /proc/loadavg 负载情况
性能参数
1)top
M:按内存使用排序
P:按CPU占用排序
1:显示各CPU的使用情况
k:kill进程
o:更多排序规则
回车:刷新数据
2)ulimit
ulimit -a:显示本用户的系统限制参
- [经营与资产]保持独立性和稳定性对于软件开发的重要意义
comsci
软件开发
一个软件的架构从诞生到成熟,中间要经过很多次的修正和改造
如果在这个过程中,外界的其它行业的资本不断的介入这种软件架构的升级过程中
那么软件开发者原有的设计思想和开发路线
- 在CentOS5.5上编译OpenJDK6
Cwind
linuxOpenJDK
几番周折终于在自己的CentOS5.5上编译成功了OpenJDK6,将编译过程和遇到的问题作一简要记录,备查。
0. OpenJDK介绍
OpenJDK是Sun(现Oracle)公司发布的基于GPL许可的Java平台的实现。其优点:
1、它的核心代码与同时期Sun(-> Oracle)的产品版基本上是一样的,血统纯正,不用担心性能问题,也基本上没什么兼容性问题;(代码上最主要的差异是
- java乱码问题
dashuaifu
java乱码问题js中文乱码
swfupload上传文件参数值为中文传递到后台接收中文乱码 在js中用setPostParams({"tag" : encodeURI( document.getElementByIdx_x("filetag").value,"utf-8")});
然后在servlet中String t
- cygwin很多命令显示command not found的解决办法
dcj3sjt126com
cygwin
cygwin很多命令显示command not found的解决办法
修改cygwin.BAT文件如下
@echo off
D:
set CYGWIN=tty notitle glob
set PATH=%PATH%;d:\cygwin\bin;d:\cygwin\sbin;d:\cygwin\usr\bin;d:\cygwin\usr\sbin;d:\cygwin\us
- [介绍]从 Yii 1.1 升级
dcj3sjt126com
PHPyii2
2.0 版框架是完全重写的,在 1.1 和 2.0 两个版本之间存在相当多差异。因此从 1.1 版升级并不像小版本间的跨越那么简单,通过本指南你将会了解两个版本间主要的不同之处。
如果你之前没有用过 Yii 1.1,可以跳过本章,直接从"入门篇"开始读起。
请注意,Yii 2.0 引入了很多本章并没有涉及到的新功能。强烈建议你通读整部权威指南来了解所有新特性。这样有可能会发
- Linux SSH免登录配置总结
eksliang
ssh-keygenLinux SSH免登录认证Linux SSH互信
转载请出自出处:http://eksliang.iteye.com/blog/2187265 一、原理
我们使用ssh-keygen在ServerA上生成私钥跟公钥,将生成的公钥拷贝到远程机器ServerB上后,就可以使用ssh命令无需密码登录到另外一台机器ServerB上。
生成公钥与私钥有两种加密方式,第一种是
- 手势滑动销毁Activity
gundumw100
android
老是效仿ios,做android的真悲催!
有需求:需要手势滑动销毁一个Activity
怎么办尼?自己写?
不用~,网上先问一下百度。
结果:
http://blog.csdn.net/xiaanming/article/details/20934541
首先将你需要的Activity继承SwipeBackActivity,它会在你的布局根目录新增一层SwipeBackLay
- JavaScript变换表格边框颜色
ini
JavaScripthtmlWebhtml5css
效果查看:http://hovertree.com/texiao/js/2.htm代码如下,保存到HTML文件也可以查看效果:
<html>
<head>
<meta charset="utf-8">
<title>表格边框变换颜色代码-何问起</title>
</head>
<body&
- Kafka Rest : Confluent
kane_xie
kafkaRESTconfluent
最近拿到一个kafka rest的需求,但kafka暂时还没有提供rest api(应该是有在开发中,毕竟rest这么火),上网搜了一下,找到一个Confluent Platform,本文简单介绍一下安装。
这里插一句,给大家推荐一个九尾搜索,原名叫谷粉SOSO,不想fanqiang谷歌的可以用这个。以前在外企用谷歌用习惯了,出来之后用度娘搜技术问题,那匹配度简直感人。
环境声明:Ubu
- Calender不是单例
men4661273
单例Calender
在我们使用Calender的时候,使用过Calendar.getInstance()来获取一个日期类的对象,这种方式跟单例的获取方式一样,那么它到底是不是单例呢,如果是单例的话,一个对象修改内容之后,另外一个线程中的数据不久乱套了吗?从试验以及源码中可以得出,Calendar不是单例。
测试:
Calendar c1 =
- 线程内存和主内存之间联系
qifeifei
java thread
1, java多线程共享主内存中变量的时候,一共会经过几个阶段,
lock:将主内存中的变量锁定,为一个线程所独占。
unclock:将lock加的锁定解除,此时其它的线程可以有机会访问此变量。
read:将主内存中的变量值读到工作内存当中。
load:将read读取的值保存到工作内存中的变量副本中。
- schedule和scheduleAtFixedRate
tangqi609567707
javatimerschedule
原文地址:http://blog.csdn.net/weidan1121/article/details/527307
import java.util.Timer;import java.util.TimerTask;import java.util.Date;
/** * @author vincent */public class TimerTest {
- erlang 部署
wudixiaotie
erlang
1.如果在启动节点的时候报这个错 :
{"init terminating in do_boot",{'cannot load',elf_format,get_files}}
则需要在reltool.config中加入
{app, hipe, [{incl_cond, exclude}]},
2.当generate时,遇到:
ERROR